Блуждание фотона
Ниже мы рассмотрим простейшую физическую задачу диффузии фотонов из недр звезды наружу и ознакомимся с двумя важнейшими физическими величинами — длиной свободного пробега и коэффициентом непрозрачности.

Представьте себе частицу, которая летит внутри газа из других частиц с концентрацией n. Пусть эта частица может взаимодействовать лишь с теми частицами, которые находятся недалеко от нее, в круге с центром в рассматриваемой частице и площадью σ. Сколько взаимодействий произойдет, пока частица пролетает расстояние dx?
Очевидно, что взаимодействий будет столько же, сколько частиц попадет в «трубочку» длины dx и площадью сечения σ, то есть n·dx·σ.
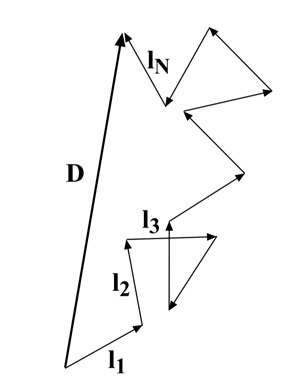
Рис. 2. Блуждание фотона в недрах звезды. Каждый шаг l1, l2 и т. д. — случайный, в результате через N шагов частица пролетает некоторое расстояние D
Если теперь приравнять это выражение к 1, то dx будет выражать длину, на которой в среднем происходит ровно одно взаимодействие — это так называемая длина свободного пробега l = 1/(nσ). Параметр σ называется сечением взаимодействия, оно определяется микрофизикой конкретного взаимодействия, и здесь мы в эти подробности вдаваться не будем. Иногда равенство для длины свободного пробега записывают в виде l = 1/(ρκ), используя параметры с другими размерностями: ρ — плотность, а κ — коэффициент непрозрачности. Для более глубокого понимания этих физических понятий предлагается сперва решить или хотя бы просмотреть задачу Столкновение фотонов, в которой обсуждается сечение фотон-фотонного взаимодействия и длина свободного пробега.
Самым «популярным» типом рассеяния фотонов в недрах Солнца является томсоновское рассеяние фотона на свободном электроне. Сечение такого взаимодействия равно σT = 6,7×10−25 см2.
Теперь представьте, что где-то в центре звезды излучился фотон. Он, естественно, не может свободно распространяться в плотной ионизованной внутренности звезды и поэтому будет постоянно рассеиваться. Путь фотона будет устроен как случайное блуждание со случайным шагом (рис. 2).
Задача
1) Приняв, что рассеяние фотонов в недрах Солнца в основном обусловлено томсоновским взаимодействием, вычислите характерную длину свободного пробега фотона. Считайте, что Солнце состоит только из полностью ионизованного водорода.
2) Пусть фотон сделал N шагов случайного блуждания (в среднем длина каждого шага равна длине свободного пробега). Какое в среднем расстояние он пролетит?
3) Оцените время, за которое фотон, рожденный в самом центре Солнца, покинет его пределы.
Подсказка
Заметим, что на рис. 2 полный путь, выраженный вектором D — это сумма маленьких шажков li. Каждый такой шажок, который фотон делает на i-м шаге до столкновения, случаен. Если рассмотреть много-много фотонов, которые таким образом движутся, то в среднем направление этого i-го шага может быть произвольным, так как фотон может рассеяться в любом направлении. Поэтому если усреднить эти i-е «шаги» всех фотонов, то получится ноль.
Точно так же, если просто усреднить для всех разных фотонов полный путь D, который является суммой отдельных шажков, то тоже получится ноль (как сумма нулей).
Поэтому нужно вспомнить, что если направление каждого шага произвольно, то длина каждого шага в среднем равна длине свободного пробега l. Учитывая, что квадрат длины вектора — это скалярное произведение этого вектора с самим собой, то можно догадаться, что нужно сделать с D до того, как усреднять.
Решение
1) Будем пользоваться формулой l = 1/(nσ) для длины свободного пробега, где σ — сечение томсоновского рассеяния, а n — концентрация электронов, которая равна в точности концентрации протонов, так как мы считаем, что Солнце — полностью ионизованный водород. Соответственно полное число электронов (протонов) Ne = M☉/mH, а их концентрация равна ne = N/V☉, где V☉ — объем Солнца.
Таким образом, для Солнца со средней концентрацией электронов ne имеем, что длина свободного пробега фотона равна l = 1/(neσT) ≈ 1,8 см.
В реальности длина свободного пробега примерно в 20 раз меньше из-за наличия других эффектов, о которых мы поговорим в послесловии.
2) Для решения этого пункта представим вектор D в виде суммы векторов — шагов случайного блуждания: D = l1 + l2 + ... + lN.
Возведем это равенство в квадрат, то есть умножим вектор на себя скалярно. Слева будет просто-напросто длина вектора в квадрате, а справа, как нетрудно убедиться, помимо квадратов длин шагов li2 вылезут перекрестные скалярные произведения l1·l2, l1·l3 и т. д.
Теперь это равенство нужно усреднить. Физически это означает, что мы будем пускать много-много фотонов из центра Солнца и смотреть, чему в среднем равны значения li2 и скалярные произведения пар векторов. В среднем каждое li2 равно l2, а скалярные произведения в среднем обнуляются, так как направления этих векторов абсолютно произвольны. Получим тогда, что D2 = l2 + l2 + ... + l2 = N·l2, где N — это количество шагов.
То есть \( D=\sqrt{N} l \).
3) Средняя длина свободного пробега внутри Солнца у нас получилась равной l ≈ 1,8 см. Положив D = R☉, найдем, что за N = R☉2/l2 шагов фотон долетит от центра Солнца до края. Чтобы перевести это во время, учтем, что на каждый шаг фотон тратит времени l/c, и получим: (R☉2/l2)·(l/c) ≈ 2800 лет.
На самом деле, как было указано выше, реальная средняя длина свободного пробега в 20 раз меньше, поэтому реальное время вылета примерно 57 000 лет.
Получается, что фотон, произведенный в недрах Солнца доходит до нас только через 50 000 лет после своего рождения. Иными словами, если кто-то вдруг магическим образом выключит термоядерный «реактор» в центре Солнца, то мы несколько десятков тысяч лет не будем об этом подозревать.
Послесловие
Давайте подведем небольшой итог сказанному выше. Рассеяние фотонов, родившихся в результате термоядерных реакций в недрах Солнца, замедляет их вылет наружу. Соответственно, движение фотонов внутри Солнца описывается как диффузия — случайное блуждание — с некоторым шагом, называемым длиной свободного пробега, который равен l = 1/(nσ) = 1/(ρκ), где κ — коэффициент непрозрачности, а σ — сечение рассеяния.

Рис. 3. Рассеяние фотона на свободном электроне (томсоновское рассеяние)
В случае, когда рассеяние только томсоновское, то есть электроны в основном рассеиваются на свободных электронах (рис. 3), коэффициент непрозрачности (и сечение рассеяния) никак не зависит от температуры или плотности. Такое приближение хорошо работает при очень высоких температурах (рис. 6).
При более низких температурах, когда часть протонов все еще находится в составе атомах (частичная ионизация), возможны другие более эффективные рассеяния и поглощения фотонов. Например, фотоны определенных энергий могут поглощаться связанными электронами в атоме, которые из-за этого переходят на более «высокие» энергетические уровни (рис. 4). В таком случае говорят, что фотон возбудил атом. Такое поглощение называют bound-bound (то есть «связный-связный» — атом из связного состояния переходит в связное, ничего не ионизируется).

Рис. 4. Поглощение фотона связанным электроном и возбуждение атома. Рисунок с сайта fysikcbogen.systime.dk
Кроме этого, если энергия фотона будет достаточно высокой, электрон может не просто перейти на более «высокий» уровень, но и оторваться от атома — атом ионизируется. Такой процесс иногда называют фотоионизацией или bound-free процессом («связный-свободный»).
Если есть bound-bound и bound-free, то, наверное, есть и free-free? Да, но этот процесс чуть более сложный. В физике давно известен процесс, когда заряженная легкая частица, например, электрон, ускоряется в поле иона (протона). Ускорение заряженной частицы обязательно сопровождается излучением фотона; такое излучение называют тормозным или чаще всего по-немецки — bremsstrahlung (рис. 5, слева).

Рис. 5. Прямое (слева) и обратное (справа) тормозное излучение (bremsstrahlung)
Микрофизические процессы всегда обратимы, поэтому возможен и обратный процесс, а именно, поглощение фотона одновременно несвязными электроном и ионом (рис. 5, справа). Такой процесс называют free-free поглощением.
Таким образом, при низких температурах, если учесть все эти поглощения, то коэффициент непрозрачности имеет следующую функциональную зависимость от плотности и температуры (закон Крамерса, правая «спадающая» часть графика на рис. 6)
\[ \kappa\sim \frac{\rho}{T^{7/2}}. \]
При еще более низких температурах, к примеру, у поверхности звезд, когда помимо атомов могут существовать также молекулы и ионы H− (водород с дополнительным электроном), основная часть поглощения происходит именно за их счет. При этом, коэффициент непрозрачности возрастает с температурой по закону κ ~ T4 (левая, «возрастающая» часть графика на рис. 6). Оказывается, что такой режим поглощения фотонов очень важен в атмосферах красных гигантов и протозвезд (звезд, которые еще находятся в состоянии сжатия, и в центре которых еще нет интенсивных термоядерных реакций).

Рис. 6. Измеренные в лаборатории значения коэффициента непрозрачности водорода в зависимости от температуры. Различные кривые соответствуют различным плотностям. Видно, что в правой части графика они выходят на постоянное значение, это режим томсоновского рассеяния (κ ~ const). При более низких температурах работает режим Крамерса \(\kappa\sim \frac{\rho}{T^{7/2}}\). При температурах меньше ~ 8×103 K рассеяние в основном происходит из-за наличия ионов H− и молекул по закону \( \kappa\sim \rho^{1/2}T^4 \). Рисунок из книги S. Chandrasekhar, An Introduction to the Study of Stellar Structure
Вооружившись этим знанием, в одной из следующих задач увидим, почему все звезды главной последовательности с массами от 0,1 до 100 масс Солнца ложатся на одну линию на диаграмме Герцшпрунга — Рассела и выведем форму этой линии.
При подготовке задачи использовалась книга D. Maoz, Astrophysics in a Nutshell.
-
Нет, естественно никакого эксперимента нет. Но всё довольно логично, так как мы достаточно хорошо представляем все эти процессы рассеяния.
-
Конечно логично, в рамках этой простой модели. На сколько изменится ответ этой задачи, если мы добавим идею, что концентрация электронов и протонов уменьшается по мере удаления от центра нашей модели Солнца?
Если я свечу фонариком на солнце, то можно ли утверждать что какие то фотоны достигнут центра Солнца через 57 000 лет и потом столько же потратят чтоб убежать оттуда?
Если теоретически это происходит, то мы можем увидеть одну звезду сквозь другую (без гравитационного линзирования)?
А если вернуться к реальности, на что влияет оценка времени прохождения фотонов внутри солнца? Что это нам дает?-
1. Не сильно изменится, ну т.е. не на порядок. Помимо концентрации, меняется ещё температура, вблизи поверхности появляются конвекционные потоки и т.д. Но это всё не сильно влияет на характерное время, оно где-то от 10 до 100 тысяч лет.
2. Из вашего фонарика эффективно до центра Солнца не дойдёт ни один фотон, так как вероятность прохождения ничтожная, а фотонов очень мало.
3. Не можем, по той же причине.
4. Сама эта оценка нам даёт какое-то дополнительное характерное время, соответствующее диффузии фотонов из недр до поверхности. Это время можно сравнивать, например, с характерным конвективным временем, динамическим временем перестройки плотности при возмущениях и т.д.
В случае с Солнцем эти времена очень далеки друг от друга, поэтому все эти процессы происходят на разным временным масштабах и не влияют друг на друга, но в принципе в каких-то других системах они могут быть порядка друг друга, и тогда нужно учитывать всё вместе.-
Мы же говорим только о вероятностях по сути. Поэтому вы не можете утверждать "до центра Солнца не дойдёт ни один фотон". Рано или поздно дойдет. Иначе вы отрицаете саму суть физики как науки.
Мы берем миллиарды лет. Берем две звезды. Одна загораживает другую. Та что дальше может быть намного ярче и больше.
Пролетают ли фотоны от дальней звезды сквозь ближнюю? Очевидно что да. )) Чем ближе к центру звезды тем, по идее, меньше фотонов пролетает. Если поток фотонов зацепит край то пройдет с наименьшими потерями и рассеянием. Если попадает в центр то вероятность стремится к нулю, как вы и сказали.
Тогда мы с вами вместе можем выдвинуть гипотезу, что можно отыскать такие звезды и изучить изменение из цвета к центру. Для красоты можно даже предположить что мы увидим что то наподобие интерференционных колец.
Просто я не натыкался нигде на такие модели. Т.е. как меняется цвет звезды если за ней светит еще другая и большая?
Вот на такие идеи меня подтолкнул ваш ответ )))-
Ну можете посчитать, сколько вам нужно держать фонарик, чтобы хоть один фотон добрался до центра. Вангую, что окажется много больше жизни Вселенной.
Проблема такого наблюдения по краю - техническая, т.е. вам надо разрешать большой диапазон светимостей, чтобы уметь на фоне Солнца увидеть другую звезду. Для этого обычно Солнце просто загораживают коронографом.
Ещё раз, чтобы увидеть хотя бы один фотон от звезды позади, вам надо смотреть непрерывно огромное количество времени. Т.е., условно, на 10^10 фотонов одной звезды будет приходится один фотон другой. Это несущественно и поэтому абсолютно неинтересно. Никакой гипотезы строить не надо.-
Видимо это и есть следующая задачка ))) И я бы не спешил с такими жесткими оценками, так как все зависит от модели которую вы выбираете.
Очевидно что ни Солнце, ни другие звезды не могут быть идеальными объектами. А теории их устройства - это плод нашей фантазии и логики. Мы даже толком не знаем что у нас под ногами. Просто верим... )))
Если взять слоистую модель Солнца, то расчеты могут привести к совсем неожиданным результатам.
Внутри слоя можно применить и вашу логику расчета времени убегания. а вот переход между слоями уже носит скачкообразный характер и тут может оказаться, что фотоны рожденные в центре практически никогда не вылетают за пределы. Вернее время убегания стремится к бесконечности.
И вероятность к нулю.
Т.е. усложнив чуть-чуть вашу модель, мы можем получить полностью противоположный результат.
Это реально?-
Нет, абсолютно никак. Есть достаточно точные модели устройства звёзд, они предсказывают, например, поток нейтрино с точностью до долей процентов. Так что всё отлично, никакой фантазии тут нет. Модели отлично работаю и соответствуют действительности.
-
Модель в физике - это не реальность. Модель - это плод работы фантазии в совокупности с принятой логикой. Модели подгоняются под факты взятые из экспериментов.
Нейтрино имеет длину свободного пробега в воде как я помню 10^18 метров (сотня световых лет). А у фотона все наоборот.
Так что предлагаю вам не использовать жесткие "нет", "никогда", "абсолютно никак".
Это просто скучно и не дает никакого шанса на развитие и хоть маленький шаг вперед.
Сама физика как наука - это модель, сложенная из кучи разных других моделей. Причем это очень живая куча. Постоянно меняется, что то обновляется, уточняется и даже отмирает.
Это просто один из способов смотреть на мир.
Никто не видел атомы. Это модель. Мы смотрим на их тени на плоской поверхности.
С какой точностью можно узнать вас как человека, глядя на вашу тень? И предсказать ваше поведение? )))
Я веду к тому что в реальности Солнце - это объект гораздо сложнее чем наша планета. Так же как и наша планета гораздо сложнее чем, например ваше тело или клетка. Так что выбор модели и принятие их как "реальности" может просто закинуть вас в группу верующих фанатиков, но никак не естевствознателей и ребят которые с шутками и весельем познает мир вокруг.
Просто нет смысла с серьезным выражением лица обсуждать то чего нет в реальности ))).
А в реальности нет одинаковых объектов. Нет полностью одинаковых людей, нет одинаковых песчинок или звезд.
Есть такая логика, что если бы и атомы были одинаковые, то мы бы наблюдали на нашем уровне тоже абсолютно одинаковые объекты.
Что выдумаете на этот счет? ))-
Вы занимаетесь не физикой, а пустозвонством. Предлагаю вместо огромного количество бессмысленных слов взять и руками посчитать всё самостоятельно. Почитайте книжки по физике звёзд, там всё отлично описано. Могу предложить отличный учебник: http://www.springer.com/us/book/9783642302558. Почитайте, хотя бы несколько глав, после этого диалог будет куда более содержательный.
-
Я продолжаю веселиться ))
Вы делаете утверждения, не соответствующие реальности. И даже не хотите их как то просто обосновать. Хотя бы в шутку.
Более того, вы даже не знаете с кем общаетесь )))
Может Руди мой наставник и учитель. А вы мне его же книжку и предлагаете. )))
Если вы до конца разобрались в теории Киппенхана, то сможете сказать где тут есть нерешенные проблемы и дыра, которую нельзя ни опровергнуть ни доказать.
Если вам кажется что эта книга и есть конечная истина, то Руди посмеется над вами вместе со мной ))
У него лично есть и совершенно альтернативные взгляды на мир вокруг.
Вы в данном случае ничем не отличаетесь от религиозных фанатиков, которые посылают всех вокруг читать библию или другие тексты, ставя себя выше других и считая себя умнее, не утруждаясь обосновывать свою точку зрения.
Кстати по моей статистике, серьезные теоретики и реальные копатели наук, обычно большие приколисты и шутники с очень широким взглядом на мир и знаниями... просто юмор у них бывает очень специфическим. ))
Так что улыбнитесь и менее серьезно относитесь к чужим теориям. И апелляция к авторитетам и книжкам - самой плохой способ защиты своих взглядов. Это чисто мои реальные наблюдения за серьезными и интересными спорами о мире вокруг.
Все что я сказал не противоречит идеям Рудольфа. И я в свое время, написал кучу программного кода для просчета разных моделей и звезд и черных дыр и т.д.
Так получилось что на тот момент мои совокупные знания и интерес в программирование и теор физике оказались очень востребованы почти по всему миру.
Над какой задачей вы сейчас реально работаете? Вы делаете что то, что до вас никто не делал? Или все еще идете по следам наших учителей и проложенным тропкам?
-
-
-
-
-
-
-
-
-
-
-
нет, константа вылезает и для миллиарда. При броуновском движении матожидание максимального перемещения превышает матожидание итогового перемещения. Говоря в терминах, близких мне по специальности - этот пример мне кажется удачным потому, что он прямо соотносится с бытовым опытом, хотя математика у него ровно та же самая, что и у рассеянного фотона, заблудившегося человека, броуновской частицы, разорённого игрока и еще кучи классических задач - так вот, размах спутанной нитки в модели случайных блужданий заметно превышает расстояние между ее концами. В случае фотонов, идущих из центра Солнца, нас интересует время, когда фотон впервые достигнет поверхности Солнца, потому что в этот момент случайные блуждания для него закончатся. Хотя на самом деле эта поправка почти ничего не меняет, это гораздо более сложная задача, и лично мне как раз из общих соображений не очевидно, что формула с точностью до небольшой константы останется той же.
-
Да, это примерно как в задачах о разорении игрока или в задаче о пьяном матросе у обрыва: нас интересует не среднее перемещение через N шагов в "приближении" отсутствия обрыва, впоследствии приравненное к расстоянию до обрыва, а матожидание числа шагов, впервые приводящих к достижению обрыва.
-
Для одномерного случая формула мат-ожидания перемещения точная (gaussian random walk). Для трёхмерного случая добавится какая-нибудь константа, да.
-
Да нет же. Дело не в трехмерии. Трехмерие как раз в случае дискретного блуждания шагами равной длины ни к какому коэффициенту не приведет. Дело в том, что это разные задачи: перед вами стоит задача running maximum of a random walk, а вы решаете задачу о среднем расстоянии (даже о среднем квадрате расстояния: средний модуль расстояния тоже отличается в константу). И хотя задача о максимуме (она же и задача о first hitting time) даёт ту же зависимость, а в одномерном случае и ту же константу 1, что и ваше решение, это всё-таки другая, гораздо более хитрая задача. То, что в ней тоже вылезает именно корень из N, а не что-то другое - не очевидно и требует объяснения.
-
Окей, я кажется понял о чём вы. Дело в том, что здесь нет такой чёткой границы выхода фотона из Солнца (как в случае с пьяным моряком). Нет такого момента, после которого вы говорите, что фотон покинул Солнце. Более того, средний шаг фотона сильно зависит от того где он находится и т.д. Мы пренебрегаем очень многим.
Поэтому для упрощения достаточно рассмотреть задачу, что среднеквадратичное расстояние блуждания порядка радиуса звезды. По порядку величины ответ отличаться будет не сильно.
-
-
-
-
Последние задачи















Рис. 1. Иллюстрация физического смысла сечения взаимодействия