Куда девался эксцентриситет?
Февраль этого года принес выдающееся астрофизическое открытие: после десятилетий поисков были напрямую зарегистрированы гравитационные волны. Более того, по форме всплеска, пойманного гравитационно-волновой обсерваторией LIGO, физики смогли узнать, что родились эти волны при слиянии двух черных дыр (рис. 1), и даже умудрились оценить их массы и вращение. По сути, в одной короткой статье физики сделали сразу два открытия нобелевского уровня: подтвердили предсказание Эйнштейна 1916 года и положили начало гравитационно-волновой астрономии. Подробный рассказ о тех открытиях читайте в наших новостях Гравитационные волны — открыты! и LIGO поймала новые всплески гравитационных волн.

Если сам факт регистрации гравитационных волн — это чисто инженерный подвиг, то второе достижение — восстановление характеристик черных дыр по их гравитационно-волновому «звучанию» — опирается на общую теорию относительности. Дело в том, что слияние черных дыр однозначно рассчитывается теоретически. Зная массы и вращение двух черных дыр, а также параметры орбиты, теоретики могут предсказать профиль гравитационно-волнового всплеска. Выполнив такие расчеты-предсказания для разных параметров и сравнив их с формой пойманного в детекторе всплеска, физики находят самый подходящий профиль и узнают тем самым, слияние каких объектов его породило (рис. 2).

Рис. 2. Теоретически восстановленная форма гравитационно-волнового всплеска для события GW151226. Рисунок из статьи LIGO Scientific Collaboration and Virgo Collaboration, 2016. GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence
Вооружившись этой информацией и прочитав внимательно наши новости, дотошный читатель может заметить одну странность — в новостях нигде не говорится про форму орбиты. Физики тщательно учитывают массы черных дыр и их вращение вокруг собственной оси. Но вот орбиту, по которой две черных дыры двигались перед слиянием, они считают круглой. Возникает ощущение, что физики «забыли» школьную физику: ведь все знают, что тела могут двигаться в поле тяжести не только по кругу, но и по эллипсу, в одном из фокусов которого находится центр притяжения, а точнее, центр масс двух тел (см.: Законы Кеплера).
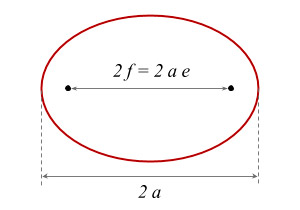
Рис. 3. Эксцентриситет эллипса равен расстоянию между двумя фокусами, деленному на длину большой оси. Здесь показан эллипс с эксцентриситетом e ≈ 0,8
Для удобства обсуждения напомним, что вытянутость эллипса характеризуется эксцентриситетом e. Он равен расстоянию между двумя фокусами, поделенному на большую ось эллипса (рис. 3). Для круглой траектории e = 0, для умеренно вытянутой — несколько десятых, для экстремально вытянутой — он близок к единице. Так вот, когда ученые восстанавливали параметры черных дыр по данным LIGO, они не учли, что у орбиты есть ненулевой эксцентриситет.
Конечно, речь тут не идет ни о каком «грубом просчете», как бы того ни желали разные ниспровергатели современной физики. Ученые вовсе не «забыли» об эксцентриситете орбиты, а на основании некоторых аргументов посчитали, что его учитывать не нужно. И в этой задаче, по сути, требуется восстановить эти аргументы. Для простоты картины мы предполагаем, что все внешние воздействия на пару гравитационно-связанных черных дыр отсутствуют: нет ни межзвездного газа, ни пролетающих мимо других объектов. У нас чистая задача двух тел — правда, с учетом гравитационного излучения.
Задача
Объясните, почему физики в анализе данных LIGO не стали учитывать эксцентриситет орбиты сливающихся черных дыр.
Примечание. Для сомневающихся читателей подчеркнем, что для решения задачи не требуется быть физиком и уметь рассчитывать слияние черных дыр. Достаточно «чувствовать» обычные законы небесной механики и внимательно разобраться с новостями про LIGO.
Подсказка 1
Скажем сразу, что простая попытка списать это на то, что эксцентриситет якобы не влияет на форму гравитационно-волнового всплеска, — не работает. Влияет, и еще как! На рис. 4 показаны теоретически рассчитанные профили гравитационно-волнового всплеска, который пришел бы от двух объектов звездных масс, если бы в последние мгновения перед слиянием они двигались бы по круговой (e = 0, красный график), вытянутой (e = 0,5, синий и желтый графики), и сильно вытянутой орбите (e = 0,9, зеленый и розовый графики).

Рис. 4. Теоретически рассчитанная форма гравитационно-волнового всплеска для орбит с разными параметрами. Рисунок с сайта soundsofspacetime.org
Как видно, эффект очень важен. Так почему же физики не приняли его в расчет?
Подсказка 2
Из предыдущих замечаний следует единственный вывод: у физиков есть убедительные аргументы в пользу того, что эксцентриситет пренебрежимо мал, то есть что орбиты двух черных дыр в последние мгновения перед слиянием были очень круглые. Но позвольте, мы же не знаем, как эта пара черных дыр образовалась! Вполне могло получиться так, что, за миллионы лет до этого две черные дыры, объединившись в гравитационно-связанную пару, «сели» на очень вытянутую орбиту.
С этой возможностью никто не спорит: исходный эксцентриситет вполне мог быть большим. Физики лишь утверждают, что непосредственно перед слиянием орбита уже может считаться круглой. Значит, должен существовать какой-то способ «устранить» лишний эксцентриситет, как бы округлить орбиту в процессе эволюции. И способ этот должен быть железобетонным и не зависящим от каких-то внешний условий.
Подумайте теперь, как так получается, что в процессе сближения пара черных дыр не просто становится теснее, а выходит на все более круглую орбиту.
Подсказка 3
Единственный процесс, способный, в условиях нашей задачи, влиять на параметры орбиты — это само излучение гравитационных волн. Представьте себе два компактных объекта на сильно вытянутой орбите друг вокруг друга. Для динамики движения совершенно несущественно, что это две черных дыры; вам достаточно лишь почувствовать и применить обычные законы небесной механики. Поглядывая на графики всплеска, попытайтесь понять, в какой момент орбитального движения гравитационные волны испускаются сильнее всего. Затем остается сделать последний шаг — понять, почему потеря энергии преимущественно в эти моменты приводит к округлению орбиты. И для этого опять достаточно лишь чувствовать общие законы небесной механики.
Решение
Все закономерности, которые мы обсуждаем ниже, могут быть записаны в точных формулах, и с этим может справиться и студент-физик. Но поскольку это задача на качественное понимание явления, мы специально будем избегать формул, напирая на физическую интуицию.
Прежде всего, динамика тела на сильно вытянутой эллиптической орбите должна быть понятна из многочисленных примеров движения тел в Солнечной системе. Гравитирующее тело (а точнее, центр масс двух тел) находится в фокусе эллипса. Когда тело приближается к нему, оно ускоряется, проскакивает перицентр на максимальной скорости, затем удаляется, замедляется, в апоцентре (на максимальном удалении) ползет медленнее всего, затем начинает возвращаться и ускоряться.
Приведенный выше график гравитационно-волнового всплеска ясно говорит о том, что чем теснее пара, то есть чем быстрее движутся друг относительно друга две черные дыры, тем сильнее излучение (см. резкое усиление непосредственно перед слиянием). Это значит, что на очень вытянутой орбите самый сильный выброс гравитационного излучения происходит в перицентре, когда два тела пролетают близко друг к другу на максимальной скорости и резко разворачиваются. Те узкие пики, которые видны на двух нижних графиках на рис. 4, как раз отвечают этим событиям. На дальних участках траектории тело движется медленно, разворачивается неторопливо, и, даже несмотря на длительное время, проведенное вдалеке, вклад в излученную энергию волн там незначителен.
Следующий шаг. Излучая гравитационные волны, пара черных дыр теряет энергию. Для круговой орбиты, когда излучение идет равномерно, общий эффект простой: пара сближается и ее вращение ускоряется. Кинетическая энергия возрастает, потенциальная — уменьшается вдвое быстрее, поэтому полная энергия тоже становится все более и более отрицательной.

Рис. 5. Резкая потеря в перицентре энергии на излучение гравитационных волн приводит к тому, что на следующем витке апоцентр приблизится
Но при сильно вытянутой орбите картина меняется. Энергия теряется не равномерно, а как бы импульсами, в момент прохождения перицентра. Результат такого импульсного излучения — потеря скорости в этот момент. Тела снова разлетаются, но уже чуть медленнее. А это значит, что на следующем витке апоцентр уже лежит ближе, чем раньше. Перицентр почти не изменился, апоцентр — приблизился, следовательно, эксцентриситет уменьшился. И так происходит потихоньку круг за кругом, а точнее, эллипс за эллипсом. Конечно, потеря энергии происходит не строго рывками, она просто то усиливается, то ослабляется, но качественный результат будет такой же: пара сближается, ее траектория округляется, черные дыры словно «притираются» друг к другу. Так продолжается миллионы лет, и за это время любая осмысленная траектория успевает превратиться почти в идеальную окружность.
Послесловие
Конечно, все эти рассуждения требуют количественного подтверждения. Процесс излучения гравитационных волн при движении двух гравитационно-связанных тел по эллиптической орбите был аккуратно вычислен во всех деталях Питерсом и Мэтьюсом в 1963 году в статье P. C. Peters and J. Mathews, 1963. Gravitational Radiation from Point Masses in a Keplerian Orbit, и затем отдельно Питерсом, чуть подробнее.
Они вычислили мощность, которая тратится на излучение гравитационных волн, и сравнили случаи эллиптической орбиты с большой полуосью a и эксцентриситетом e и круговой орбиты (то же значение a, только e = 0). Оказалось, что от эллиптической орбиты излучение идет куда более мощное, причем, чем ближе эксцентриситет к единице, тем больше усиление. Затем они сосчитали темп сближения (то есть среднюю по периоду скорость уменьшения большой полуоси −da/dt) и темп округления (скорость уменьшения эксцентриситета −de/dt). Оказалось, что одно связано с другим, и приближенно эта зависимость выглядит так:
Иными словами, даже если пара черных дыр в начальный момент находилась на орбите с большим эксцентриситетом, то по мере сближения пары (то есть уменьшения a) эксцентриситет тоже уменьшается, примерно пропорционально a19/12. Если за время эволюции пары с момента образования до слияния размер орбиты уменьшился, например, в 10 раз, то эксцентриситет уменьшится почти в 40 раз, и орбита станет практически круглой.
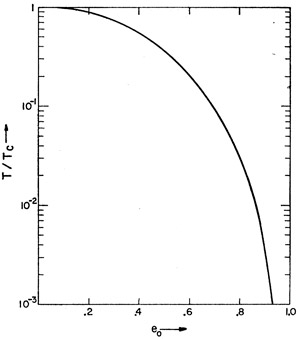
Рис. 6. Время жизни пары до слияния в зависимости от начального эксцентриситета орбиты по сравнению с круглой орбитой такого же размера. График из статьи P. C. Peters, 1964. Gravitational Radiation and the Motion of Two Point Masses
Эти расчеты, правда, опирались на предположение, что скорости тел остаются малыми по сравнению со скоростью света. В момент слияния черные дыры достигают уже релятивистских скоростей, так что к самым последним мгновениям их совместной жизни эти результаты не применимы. В этом случае придется моделировать сам процесс слияния с помощью сложнейших численных расчетов, которыми занимаются многие исследовательские группы по всему миру. Но для предыдущих миллионов лет эволюции результаты Питерса и Мэтьюса отлично описывают динамику сближения пары.
Раз эксцентриситет сильно влияет на гравитационное излучение, значит, он уменьшает время жизни пары до слияния (рис. 6). Это очень важная информация для астрофизиков. Скажем, они могут промоделировать динамику компактных объектов в большом звездном скоплении и оценить, как часто черные дыры или нейтронные звезды объединяются в пары. Но если время жизни пары до слияния очень большое, мы никогда не дождемся от них гравитационно-волнового всплеска. Приведенные выше вычисления показывают, что, оказывается, очень важно знать не только начальный размер пары, но и эксцентриситет — он может менять время жизни на порядки.
Ну и последний момент. Формулы, приведенные выше, показывают, что орбита округляется не сама по себе, а по мере сближения пары. Круглая будет орбита в конце или не очень, — зависит не только от начального эксцентриситета, но и от того, во сколько раз орбита успела сжаться до слияния. Чисто теоретически может оказаться так, что две черные дыры сразу оказались на очень тесной и сильно вытянутой орбите и уже почти готовы к слиянию. Тогда у них не будет времени для долгого процесса сближения, а значит, эксцентриситет не успеет погаситься. Вот тогда гравитационно-волновой всплеск действительно будет нести на себе отпечаток вытянутой орбиты, как на рис. 4. Дело лишь в том, что, согласно современной картине того, как образуются пары черных дыр звездных масс, такой процесс очень маловероятен. Тем не менее, физики при анализе данных LIGO все же проверили, нет ли в данных указаний на сильный эксцентриситет (см. статью, посвященную самому сильному гравитационно-волновому всплеску GW150914). Они убедились, что таких свидетельств нет. В будущем они планируют даже установить ограничение сверху на величину эксцентриситета в те последние доли секунды, когда LIGO «услышала» этот космический катаклизм.
Гравитационные волны
-
 07.07.2023Зарегистрированы низкочастотные гравитационные волныАлексей Левин • Новости науки
07.07.2023Зарегистрированы низкочастотные гравитационные волныАлексей Левин • Новости науки -
 11.06.2017Гравитационно-волновая астрофизика на маршеБорис Штерн • Библиотека • «Троицкий вариант» №11(230), 2017
11.06.2017Гравитационно-волновая астрофизика на маршеБорис Штерн • Библиотека • «Троицкий вариант» №11(230), 2017
-
 18.11.2016Гравитационные волны и познание Вселенной: LIGO, Большой взрыв и черные дырыКип Торн • Видеотека
18.11.2016Гравитационные волны и познание Вселенной: LIGO, Большой взрыв и черные дырыКип Торн • Видеотека
-
 07.10.2016«Гравитационные волны — новый канал изучения Вселенной»Интервью с Александром Полнарёвым • Библиотека • «Троицкий вариант» №17(211), 2016
07.10.2016«Гравитационные волны — новый канал изучения Вселенной»Интервью с Александром Полнарёвым • Библиотека • «Троицкий вариант» №17(211), 2016
-
 11.08.2016Открытие гравитационных волнСергей Попов • Видеотека
11.08.2016Открытие гравитационных волнСергей Попов • Видеотека
-
 25.07.2016Куда девался эксцентриситет?Игорь Иванов • Задачи
25.07.2016Куда девался эксцентриситет?Игорь Иванов • Задачи
-
 21.07.2016Эйнштейн был прав: гравитационно-волновая астрономияСергей Попов • Библиотека • «Популярная механика» №5, 2016
21.07.2016Эйнштейн был прав: гравитационно-волновая астрономияСергей Попов • Библиотека • «Популярная механика» №5, 2016
-
 20.06.2016LIGO поймала новые всплески гравитационных волнИгорь Иванов • Новости науки
20.06.2016LIGO поймала новые всплески гравитационных волнИгорь Иванов • Новости науки
-
 16.02.2016Открытие гравитационных волнУченые коллаборации LIGO из МГУ • Видеотека
16.02.2016Открытие гравитационных волнУченые коллаборации LIGO из МГУ • Видеотека
-
 14.02.2016Гравитационные волны: дорога к открытиюАлексей Левин • Библиотека • «Троицкий вариант» №4(198), 2016
14.02.2016Гравитационные волны: дорога к открытиюАлексей Левин • Библиотека • «Троицкий вариант» №4(198), 2016
Последние задачи













Рис. 1. Моделирование излучения гравитационных волн при слиянии двух черных дыр. Рисунок с сайта aei.mpg.de