Рыцарский турнир на выбывание

Попробуйте сначала ответить на те же самые вопросы для случая 4 участников турнира.

Пусть W_r — множество номеров победителей раунда r, r = 1, ..., 7. Выразите удовольствие короля (взвешенную продолжительность всех поединков на турнире) через элементы множества W_r.

Какое поведение короля максимизирует сумму элементов множества W_r? А какое — минимизирует ее?

Оценим суммарную продолжительность t_r поединков раунда r. Пусть P_r — множество всех участников раунда r, W_r — множество всех победителей раунда r, L_r — множество всех проигравших в раунде r. Тогда

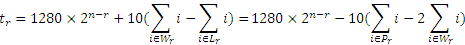
Заметим, что множество победителей текущего раунда совпадает со множеством участников следующего раунда. Пусть a — коэффициент, показывающий, во сколько раз король больше любит смотреть поединки k-го раунда по сравнению с поединком (k – 1)-го раунда. Просуммировав по всем раундам взвешенные с учетом предпочтений короля величины t_r, получим суммарное удовольствие короля от всех поединков на турнире:

Первое слагаемое является константой. Во втором слагаемом внутри скобочек, в свою очередь, первое и последнее слагаемое являются константами (первое является константой, так как множество всех участников первого раунда фиксировано, последнее является константой, так как победителем всегда является сильнейший рыцарь).

Найдем минимум суммы:

Если a > 2, то минимум достигается тогда, когда минимальна сумма номеров победителей раунда r. Очевидно, что это возможно в том и только в том случае, если это сильнейшие 2^r – 1 рыцарей. Король может добиться того, чтобы в каждом раунде побеждала сильнейшая половина рыцарей. Например, он может в каждом раунде отправлять драться сильнейшего рыцаря против слабейшего, второго сильнейшего против второго слабейшего, и так далее. Эта стратегия служит ответом к пункту в).

Если a < 2, то, наоборот, король будет стремиться сделать так, чтобы сумма номеров победителей каждого раунда была максимальной. Утверждается, что максимум суммы номеров победителей раунда r достигается при следующем наборе победителей: 1, 1 + 2^r, 1 + 2·2^r, ..., 129 – 2^r. Действительно, слабейший из победителей раунда r должен был победить в подтурнире с участием 2^r рыцарей, поэтому есть как минимум 2^r – 1 выбывший рыцарь слабее его. Второй слабейший из победителей раунда r должен был победить в подтурнире с участием 2^r рыцарей, поэтому есть как минимум еще 2^r – 1 рыцарей, более слабых, чем второй слабейший из победителей раунда r, и т. д. Указанный набор победителей для каждого раунда король может обеспечить, если в каждом раунде будет отправлять драться сильнейшего рыцаря против второго по силе, третьего — против четвертого, и т. д. Такая стратегия является оптимальной в пункте а).

Наконец, если a = 2, то удовольствие короля постоянно и не зависит от того, кто с кем дерется. Король может определять пару противников любым образом. Это является ответом на вопрос пункта б).

Некоторые условия задачи про рыцарский турнир могут показаться странными и не очень интуитивными. Например, насколько правдоподобно, что более сильный рыцарь с вероятностью 1 побеждает более слабого? Оказывается, что это условие можно немного ослабить, а найденные стратегии короля всё равно останутся оптимальными! Это следует из того, что суммарная продолжительность всех поединков на турнире непрерывно зависит от попарных вероятностей побед рыцарей друг над другом. Если p_ij — это вероятность победы рыцаря i над рыцарем j (всего необходимо задать n(n – 1)/2 вероятностей), то при небольшом изменении чисел p_ij продолжительность турнира изменится не очень сильно. С учетом конечного числа различных возможных стратегий короля, существует окрестность точки (1, 1, ..., 1) в евклидовом пространстве размерности n(n – 1)/2, такая, что для любого набора вероятностей из этой окрестности оптимальное поведение короля совпадает с его оптимальным поведением в точке (1, 1, ..., 1), то есть при предположении, что более сильный рыцарь всегда побеждает более слабого. Тем не менее найти точную границу области, в которой известно решение задачи о поведении короля, может быть проблематично. Нельзя исключать, что при наборе вероятностей p_ij, достаточно сильно отличающихся от единичных, оптимальное поведение короля будет качественно новым.

Другое предположение задачи, которое может вызывать вопросы, состоит в том, что короля интересует лишь продолжительность поединка, но не сила рыцарей, которые в нем сражаются. Можно рассмотреть обобщение задачи, при котором удовольствие короля от просмотра поединка между рыцарями i и j зависит как от продолжительности поединка, так и от величины i + j, характеризующей суммарную силу сражающихся рыцарей. Если эта зависимость носит линейный характер или «не очень сильно от него отличается», то можно показать, что по-прежнему будет существовать только два возможных оптимальных поведения короля: при достаточно большом a он снова будет в каждом раунде сталкивать половину лучших рыцарей с половиной худших, а если a будет маленьким, то королю будет выгодно всё время сталкивать друг с другом соседних по силе рыцарей.

Подробнее об этой задаче можно прочитать в работе авторов Seeding, Competitive Intensity and Quality in Knock-Out Tournaments.