Разбиение многоугольника

Алексей Доледенок
«Квантик» №9, 2022

В «Квантике» № 6 за 2022 год была опубликована задача Николая Белухова:

Какие многоугольники хоть как-то можно разбить на правильные треугольники и квадраты с единичными сторонами? Как получается, что разбиений может быть несколько, и как их тогда подсчитывать? При чём здесь вообще простое число? Давайте постепенно отвечать на эти вопросы. Для удобства будем называть квадраты и правильные треугольники плитками (по условию все стороны плиток равны 1). Все встречающиеся далее многоугольники сложены из таких плиток.

Сколько вершин?

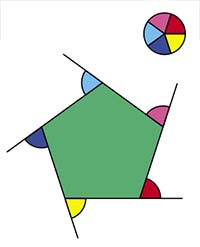
Рис. 1

Сначала поймём, что у многоугольника M не может быть слишком много вершин. Каждый угол многоугольника M либо совпадает с углом какой-то плитки, либо нет — тогда в нём стыкуется несколько плиток, то есть он составлен из углов 60° и 90°. Так как M выпуклый, его возможные углы — это 60°, 90°, 120° и 150°.

Но тогда внешние углы у М могут принимать значения лишь 120°, 90°, 60° или 30°. А сумма внешних углов любого выпуклого многоугольника равна 360° — это видно из рисунка 1 на примере пятиугольника. Даже если все внешние углы у M равны 30°, то у него будет 360°/30° = 12 вершин, а если какие-то внешние углы больше, то вершин у M будет меньше 12.

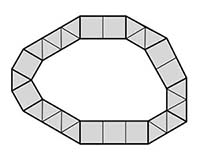
Рис. 2

Перейдём теперь к разбиениям многоугольника. Назовём каёмкой разбиения все плитки, которые имеют хотя бы одну общую точку с границей многоугольника (рис. 2).

Как устроена каёмка?

Посмотрим на плитку, которая примыкает своей стороной к стороне многоугольника — например, к AB. Если плитка квадратная, на стороне AB образуется угол 90°, который можно покрыть только квадратной плиткой. Поэтому все оставшиеся плитки, которые примыкают стороной к AB, — тоже квадраты А (рис. 3).

Рис. 3

Если же плитка треугольная, на стороне AB образуется угол 120°, который можно покрыть только двумя треугольными плитками. Поэтому все оставшиеся плитки, которые примыкают стороной к AB, — тоже треугольники (рис. 4).

Рис. 4

Если каёмка многоугольника — это не весь многоугольник, то отбросим её. Останется многоугольник поменьше. Что про него можно сказать? Если к стороне AB старого многоугольника примыкали квадраты, то соответствующая сторона CD нового многоугольника параллельна AB и имеет ту же длину (рис. 3). Если к стороне AB примыкали треугольники, то соответствующая сторона CD параллельна AB и короче неё на 1 (рис. 4).

Отдельно отметим случай, когда к стороне примыкал один треугольник. Сторона тогда просто исчезнет, но нам будет удобнее думать, что она есть, но имеет длину 0. Таким образом, стороны нового многоугольника будут параллельны сторонам исходного, а их длины будут либо такими же, либо меньше на 1. В частности, количество ненулевых сторон у нового многоугольника не больше, чем у старого, и он выпуклый.

Теперь представим, что от разбитого на плитки многоугольника оставили только контур, а границы всех плиток стёрли. Можно ли восстановить каёмку разбиения? Для ответа на этот вопрос посмотрим на какой-нибудь угол многоугольника. Если он равен 150°, плитки могут примыкать к углу двумя способами, иначе — единственным образом (рис. 5).

Рис. 5

Когда мы определимся с тем, как плитки примыкают к выбранному углу, вся остальная каёмка восстановится однозначно! И правда, сначала восстанавливается часть каёмки, примыкающая к сторонам угла, затем разбиения двух соседних углов и т. п.

Если имеется угол, отличный от 150°, начнём восстанавливать каёмку с него. Получим, что она определяется единственным образом. Отбросим каёмку. У оставшегося многоугольника количество ненулевых сторон будет не больше. Вспомним, что если у многоугольника, разбитого на плитки, меньше 12 ненулевых сторон, то у него найдётся угол, отличный от 150°. Поэтому каёмка этого многоугольника тоже определяется однозначно. Отбросим её, снова выделим каёмку и т. п. Получаем, что разбиение всего многоугольника восстанавливается однозначно!

Если же все углы многоугольника равны 150°, каёмку можно выбрать двумя разными способами (рис. 6).

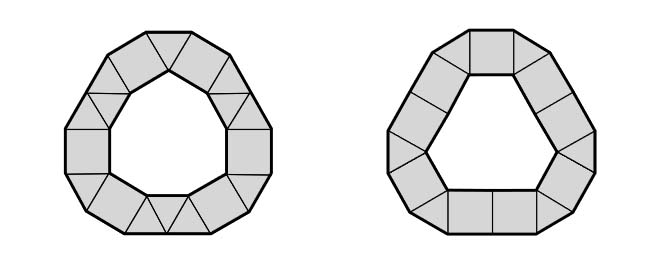
Рис. 6

Здесь и кроется причина, почему бывают многоугольники с несколькими разбиениями на плитки! Поскольку исходный многоугольник в задаче можно разбить на плитки больше чем одним способом, все его углы равны 150°, то есть M — обязательно 12-угольник.

Снимаем каёмки

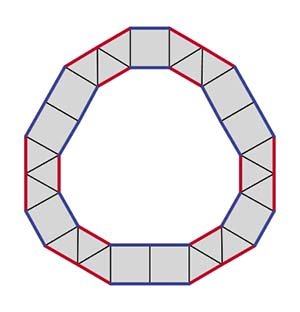
Рис. 7

Покрасим стороны M в красный и синий цвет через одну (рис. 7). Будем «раздевать» многоугольник, постепенно снимая с него каёмки, как «одёжки» с лука. Если каёмку можно выбрать двумя способами, будем выбирать один из них. Скоро мы докажем, что многоугольник, к которому мы в итоге придём, не зависит от нашего выбора!

Поскольку все углы у M равны 150°, в каёмке будут чередоваться стороны, к которым примыкают квадраты и треугольники. Значит, ко всем красным сторонам примыкают треугольники, а ко всем синим — квадраты, либо наоборот. У внутреннего многоугольника тоже покрасим стороны: если сторона CD получается из стороны AB, покрасим CD в тот же цвет, что и AB.

В итоге получим, что по сравнению с исходным многоугольником у внутреннего многоугольника длины сторон одного цвета на 1 меньше, а длины сторон другого цвета такие же.

Продолжим снимать каёмки. В какой-то момент одна из сторон исчезнет (пусть синяя, к ней тогда в последней каёмке примыкали треугольники), то есть её длина станет равна 0. Количество ненулевых сторон уменьшится, поэтому появится угол, меньший 150°. Следовательно, дальше каёмка будет определяться однозначно: к красным сторонам будут примыкать треугольники, а к синим — квадраты. Но мы и дальше будем снимать каёмки, пока возможно — то есть до тех пор, пока длина и какой-нибудь красной стороны не станет равна 0. Обозначим полученный многоугольник через N.

Чему равны длины сторон у N? Пусть r — длина наименьшей красной стороны в исходном многоугольнике M, а b — наименьшей синей. Синие стороны перестали уменьшаться в момент, когда одна из них стала равна нулю, поэтому длина каждой синей стороны уменьшилась на b. Аналогично, длина каждой красной стороны уменьшилась на r. То есть вне зависимости от того, какие каёмки мы снимали, у многоугольника N длины сторон будут одними и теми же. Кроме того, ненулевые стороны сохранили своё направление (они параллельны соответствующим сторонам исходного многоугольника M). Выходит, многоугольник N — один и тот же для разного выбора каёмок! Ведь по длинам сторон и их направлениям многоугольник можно однозначно восстановить, последовательно откладывая стороны известной длины под известными углами.

Кстати, N может оказаться просто точкой или отрезком, если последняя каёмка совпадает с последним многоугольником — это нам ничего не испортит, так как разбиение тогда уже построено полностью.

А при чём тут простое число р?

Итак, вне зависимости от того, какие мы выбираем каёмки, в итоге придём к многоугольнику N. Тогда N можно разбить на плитки (ведь мы придём к N, взяв любое исходное разбиение M). И разбивается N единственным образом (так у него уже меньше 12 сторон). Давайте ещё раз пройдём путь от M к N, снимая каёмки. Мы снимем r каёмок, уменьшающих красные стороны, и b каёмок, уменьшающих синие. Закодируем выбор каёмок: если уменьшаем красную сторону, пишем букву К, а если синюю — букву С. Получим последовательность из r букв К и b букв С. Каждой последовательности букв соответствует своя последовательность выбора каёмок, то есть своё разбиение на плитки. Поэтому всего разбиений у M столько же, сколько и таких последовательностей.

А теперь заглянем в статью «Математическая черепаха и числа сочетаний» (с. 12–15). В ней объясняется, что количество таких последовательностей равно

\(\left ( \frac{b+r}{r} \right )=\frac{(b+r)!}{b!\cdot r!}\)

Оно равно простому числу р, только если b + r = p, а r = 1 или r = р − 1 (см. задачу 8 из той же статьи).

Но если r = 1, то b = р − 1, и наоборот. Таким образом, либо самая короткая синяя, либо самая короткая красная сторона равна р − 1. Задача решена!

Художник Мария Усеинова.

Решение упражнения 1

Выделим каёмку, тут есть два варианта. Первый: треугольники примыкают к сторонам длины 1, а квадраты — к сторонам длины 2. Тогда внутри останется правильный шестиугольник со стороной 2. Как мы знаем, он разбивается однозначно — на правильные треугольники (см. рисунок). Второй вариант: треугольники примыкают к сторонам длины 2, а квадраты — к сторонам длины 1. Тогда внутри остаётся правильный 12-угольник со стороной 1. У него каёмку можно опять выделить двумя способами, в обоих случаях внутри останется правильный шестиугольник со стороной 1, который однозначно разбивается на треугольники.

Решение упражнения 2

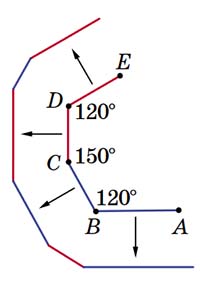
К одной стороне угла в 150° будут примыкать квадраты, а к другой — треугольники. Рассмотрим сторону, к которой примыкают квадраты. Один из них примыкает к углу в 120°. Оставшийся угол в 30° никак не покрыть плитками.

Почему же, снимая каёмки, мы не можем получить такую ситуацию? Вспомним про раскраску сторон в красный и синий цвета. Посмотрим на стороны AB и BC угла в 120°. Соответствующие им стороны исходного многоугольника (показаны на рисунке стрелками) будут идти через одну (для угла в 90° они бы шли через две, а для угла 60° — через три). Тогда они покрашены в один и тот же цвет, пусть в синий. Сторона между ними — красная.

Аналогично, у другого угла в 120° стороны CD и DE будут одноцветные. Но поскольку угол BCD равен 150°, стороны BC и CD будут разного цвета, поэтому CD и DE — красные. Но тогда между соответствующими им сторонами в исходном многоугольнике находится синяя сторона. Значит, уже обнулились и красная, и синяя стороны, то есть мы пришли к многоугольнику N, который точно можно разбить на плитки. Поэтому описанный случай не мог возникнуть.