Г. Ф. Вороной и геометрия чисел

Николай Долбилин
«Квант» №1, 2019

В этой статье мы постараемся описать общие контуры геометрии чисел — науки, которой Георгий Феодосьевич посвятил самые глубокие свои работы. Одна из них — о плотнейших упаковках шаров в многомерных пространствах — появилась на последнем году жизни. Другая — по теории параллелоэдров — была опубликована уже посмертно.

Перенесемся в 1904 год, когда в живописном немецком городе Гейдельберге состоялся третий Международный конгресс математиков. На этот конгресс пригласили выступить с докладом и Георгия Феодосьевича Вороного и Генриха Минковского (1864–1909), одного из крупнейших геометров XIX века. «Приглашенный доклад» на международном конгрессе — это очень престижное предложение, которого удостаиваются математики, добившиеся выдающихся результатов.

Минковский за 8 лет до этого, в 1896 году, опубликовал знаменитую работу «Геометрия чисел» (по-немецки Geometrie der Zahlen), в которой заложил основы новой области математики — геометрии чисел. Основная идея этой науки, находящейся на стыке геометрии и теории чисел, состоит в том, что в теории чисел есть немало задач, которые можно переформулировать на геометрическом языке, после чего задача становится более прозрачной и появляется возможность применять геометрические методы для ее решения. Самая известная, пожалуй, геометрическая теорема, которая помогает решать задачи по теории чисел, — это теорема Минковского о центрально-симметричном выпуклом теле (фигуре).

Рис. 1

Рассмотрим на плоскости прямоугольную систему координат (x, y) и множество всех целых точек, т.е. точек, у которых обе координаты — целые числа. Это множество называется квадратной решеткой (рис. 1).

Далее, фигура \( \mathscr{F} \) называется выпуклой, если для любых двух точек A и B из \( \mathscr{F} \) соединяющий их отрезок [AB] целиком принадлежит фигуре. Фигура \( \mathscr{F} \) имеет центр симметрии, т.е. такую точку O ∈ \( \mathscr{F} \), если для всякой точки X ∈ \( \mathscr{F} \) симметричная ей относительно O точка X′ также принадлежит фигуре \( \mathscr{F} \). Фигура с центром симметрии называется центрально-симметричной.

Например, круг является выпуклой центрально-симметричной фигурой, а треугольник — выпуклой, но не центрально-симметричной. Знаменитая теорема Минковского утверждает:

Пусть центр симметрии O расположен в точке решетки. Тогда если площадь фигуры s(\( \mathscr{F} \)) ≥ 4 = 2², то внутри или на границе фигуры содержится хотя бы одна пара симметричных относительно O точек решетки, отличных от точки О.

Теорема Минковского верна для любой размерности, в том числе и для кубической решетки в трехмерном пространстве. Только в этом случае речь идет о выпуклом центрально-симметричном теле \( \mathscr{F} \), объем которого v(\( \mathscr{F} \)) ≥ 8 = 2³.

Вороной и Минковский встретились и беседовали во время конгресса. Борис Николаевич Делоне слышал от отца, который тоже был приглашен на этот конгресс, что Минковский отнесся к Вороному и его работам с огромным интересом и величайшим уважением.

Геометрия чисел по духу была близка Вороному всегда: вспомним слова Делоне о том, что Вороной мыслил геометрически. В 1908 году по окончании работы над мемуаром по теории параллелоэдров Вороной писал, что работать над ним он начал лет за 12 до того, т.е. в то время, когда Минковский работал над своей «Геометрией чисел». Но полностью Георгий Феодосьевич переключился на геометрию чисел лишь после 1904 года.

Положительные квадратичные формы

Вороной создал важный метод в геометрии чисел — геометрию положительных квадратичных форм и применил ее к решению двух труднейших проблем: проблемы нахождения плотнейшей упаковки пространства равными шарами и проблемы отыскания параллелоэдров в пространствах произвольной размерности. Здесь уместно сказать, что эти проблемы в многомерных пространствах имеют не только чисто математический интерес, но и важные приложения, например в теории кодирования.

Сейчас мы постараемся объяснить связь между положительными квадратичными формами и упаковками шаров на примере плоскости. В случае двух измерений мы имеем дело с квадратичными формами от двух переменных и упаковками плоскости равными кругами.

Напомним, квадратичная форма f(x, y) от двух переменных — это однородный многочлен 2-й степени вида

f(x, y) = ax² + 2bxy + cy². (1)

Квадратичная форма f(x, y) называется положительно определенной или просто положительной, если f(x, y) > 0 для всех (x, y) ≠ (0, 0). Например, форма x² + y² очевидно является положительной, в то время как форма x² + 2xy + y² не является положительной. Заметим, что последняя форма f = (x + y)², несмотря на то, что никогда не принимает отрицательных значений, не является положительной, потому что обращается в ноль в точках (x, y) при условии x = −y.

По коэффициентам формы f(x, y) = ax² + 2bxy + cy² можно определить, положительная она или нет. Как это сделать в общем случае n переменных, излагается в университетском курсе алгебры. Но в случае двух переменных можно обойтись и «школьными» средствами. Докажем, что форма f(x, y) = ax² + 2bxy + cy² — положительная, если a > 0 и ac − b² > 0.

Для доказательства рассмотрим сначала все пары (x, y) с y = 0, т.е. пары (x, 0), где x ≠ 0. Так как a > 0, то f(x, 0) = ax² > 0 для любого x ≠ 0. Пусть теперь y ≠ 0. Тогда, обозначив \( t = \frac{x}{y} \), имеем

f(x, y) = y²(at² + 2bt + c). (2)

Сомножитель at² + 2bt + c в (2) одного знака при всех t, так как этот квадратный трехчлен не имеет корней (в силу того, что дискриминант b² − ac отрицателен). Этот трехчлен положителен, поскольку старший коэффициент a > 0.

Упражнение. Докажите обратное утверждение: если форма f(x, y) = ax² + 2bxy + y² положительная, то a > 0 и ac — b² > 0.

Положительные формы и расстояния

Ключевая идея геометрии положительных квадратичных форм, кратко ПКФ, состоит в том, что значение ПКФ f(x, y) есть квадрат длины вектора \(\overrightarrow{OA}\) или, что то же самое, есть квадрат расстояния от начала O до точки A с координатами (x, y).

Рассмотрим для примера две конкретные ПКФ:

f₁(x, y) = x² + y² и f₂(x, y) = x² + xy + y².

Сумма квадратов f₁(x, y) = x² + y² есть ПКФ и задает квадрат расстояния |OA| от начала O = (0, 0) до точки A = (x, y) в прямоугольной системе координат. Что касается формы f₂ = x² + xy + y², то ее положительность следует из того, что для ее коэффициентов оба неравенства a = 1 > 0 и \( ac − b^2 = 1 − \frac{1}{4} = \frac{3}{4} > 0 \) выполняются. Хотя это и не очевидно, форма f₂(x, y) также задает расстояние |OA|, но только если координаты (x, y) точки A рассматриваются относительно другой, вообще говоря не прямоугольной, системы координат, приспособленной к данной форме.

Рис. 2

Произвольная система координат на плоскости задается упорядоченной парой векторов \( \{\overrightarrow{e_1}, \overrightarrow{e_2}\} \), исходящих из одной точки (начала O) и не лежащих на одной прямой (рис. 2). Такую пару векторов часто называют репером.

Векторы \( \overrightarrow{e_1} \) и \( \overrightarrow{e_2} \) определяют две прямые Oe₁ и Oe₂. Через точку A на плоскости проведем прямую, которая параллельна второй прямой Oe₂. Она пересекает прямую Oe₁ в некоторой точке A₁. Так как векторы \(\overrightarrow{OA}_1\) и \( \overrightarrow{e_1} \) коллинеарны, т.е. лежат на одной прямой, то для них имеем \(\overrightarrow{OA}_1 = x · \overrightarrow{e_1} \), где x — вполне определенное число, называемое координатой точки A₁ на прямой. Проведем через A прямую, параллельную первой прямой Oe₁. Она пересекает прямую Oe₂ в точке A₂. Точно так же, как и в первом случае, \(\overrightarrow{OA}_2 = y · \overrightarrow{e_2} \), а число y является координатой точки A₂ на прямой Oe₂. Упорядоченная пара чисел (x, y) и есть координаты вектора \(\overrightarrow{OA}\) (или координаты его конца — точки A) относительно репера \( \{\overrightarrow{e_1}, \overrightarrow{e_2}\} \).

Далее, форме f(x, y) = ax² + 2bx + y² сопоставим репер \( \{\overrightarrow{e_1}, \overrightarrow{e_2}\} \) такой, что

Напомним, что \( \overrightarrow{e_1} · \overrightarrow{e_2} \) означает скалярное произведение двух векторов, т.е. \( |\overrightarrow{e_1}| · |\overrightarrow{e_2}| · \text{cos}\:\angle\overrightarrow{e_1}\overrightarrow{e_2} \). Таким образом, по форме f(x, y) задается репер, у которого заданы длины его векторов и угол между ними. Тем самым репер задан однозначно с точностью до движения.

В частности, форме f₁(x, y) = x² + y² соответствует репер, задающий прямоугольную систему координат. А репер, соответствующий форме f₂(x, y) = x² + xy + y², состоит из единичных векторов \( \overrightarrow{e_1} \) и \( \overrightarrow{e_2} \) с углом 60° между ними, так как \( ( \overrightarrow{e_1} · \overrightarrow{e_2}) = \text{cos}\:\angle\overrightarrow{e_1}\overrightarrow{e_2} = b = \frac{1}{2} \).

Важно, что в системе координат репера, заданного в (3), квадрат длины отрезка OA равен значению формы f(x, y), где (x, y) — координаты точки A:

f(x, y) = |OA|². (4)

Действительно, мы имеем

При выводе равенства (4) мы воспользовались тремя известными из школьной программы свойствами скалярного произведения векторов: свойствами распределительности, перестановочности и вынесения постоянного множителя.

Решетки

В теории чисел мы имеем дело с решениями уравнений в целых числах. В связи с этим для данного репера рассмотрим на плоскости множество Λ всех точек, обе координаты которых относительно этого репера — целые числа. Это множество называется (произвольной) решеткой. Квадратная решетка является частным случаем произвольной решетки.

Итак, по каждой положительной квадратичной форме можно построить репер, по которому, в свою очередь, однозначно строится решетка:

Например, для формы f₁ = x² + y² решетка Λ₁ построена на единичном квадрате (см. рис. 1). Получающаяся для формы f₂ = x² + xy + y² решетка Λ₂ построена, как иногда говорят, на правильном треугольнике.

Рис. 3

Чтобы лучше представить решетку, нужно взять параллелограмм, построенный на векторах репера (рис. 3), так называемый основной параллелограмм решетки, и рассмотреть разбиение плоскости на основные параллелограммы. Узлы полученной параллелограммной сетки и есть решетка.

Отметим, что соответствие между реперами и решетками однозначно только в одну сторону: каждому реперу соответствует единственная решетка Λ. Обратное неверно: в данной решетке Λ можно выбрать бесконечно много других реперов таких, что построенная на них решетка совпадает с Λ (рис. 4). Основные параллелограммы, т.е. построенные на реперах данной решетки, как нетрудно видеть, имеют одинаковую площадь s, причем s² = ac − b². В частности, для квадратной решетки Λ₁ s = 1, а для решетки Λ₂, построенной на правильном треугольнике, \( s =\sqrt{3}/2 \).

Рис. 4

Подчеркнем, что теорема Минковского о выпуклой центрально-симметричной фигуре \( \mathscr{F} \) справедлива для любой решетки, не только квадратной. При этом нужно только потребовать, чтобы площадь фигуры s(\( \mathscr{F} \)) ≥ 4s, где s — площадь основного параллелограмма данной решетки.

Упаковка плоскости кругами

Для положительной формы f(x, y) определим ее арифметический минимум m_f как minf(x, y) по всем целым (x, y) ≠ (0, 0).

Рассмотрим теперь теоретико-числовую задачу: для данной ПКФ f(x, y) нужно найти ее арифметический минимум m_f и все целые решения уравнения

f(x, y) = m_f. (5)

Переведем эту задачу на геометрический язык. По форме f находим репер (3) и решетку Λ_f. Тогда арифметический минимум m_f равен квадрату расстояния от O до ближайшей точки решетки. Целые решения уравнения (5) — это координаты точек решетки, ближайших к O.

Если в каждую точку решетки Λ_f поместить центр круга, радиус которого равен половине расстояния до ближайшей точки, т.е. \( \frac{1}{2}\sqrt{m_f} \), то некоторые соседние круги будут касаться, но никакие круги не будут перекрываться. Системы попарно неперекрывающихся кругов называются упаковками. Так как в данном случае центры кругов образуют решетку, такая упаковка называется решетчатой. Причем радиус кругов \( r_f = \frac{1}{2}\sqrt{m_f} \) — максимально возможный для данной решетки, так как любое увеличение радиуса ведет к тому, что соседние круги начнут перекрываться.

Какова доля плоскости, покрытой кругами радиуса r_f? Эта доля, или, как говорят, плотность δ_f решетчатой упаковки, равна отношению площади круга к площади s_f основного параллелограмма решетки:

В частности, если центры кругов образуют квадратную решетку Λ₁, то \( δ_1 = \frac{π}{4} = 0,7853 \)... В случае правильной треугольной решетки Λ₂ плотность упаковки больше: \( δ_2 = π/(2\sqrt{3}) = 0,9068 \)...

Нетрудно показать при помощи чисто геометрических средств, что среди решетчатых упаковок плоскости кругами плотнейшая упаковка достигается именно на правильной треугольной решетке Λ₂.

Плотнейшие упаковки пространства шарами

Мы подошли к началу дороги, ведущей к одной из центральных задач всей геометрии чисел: как найти самую плотную решетчатую упаковку многомерного пространства равными шарами. Кстати, эта задача, известная для плоскости и пространства еще со времен Древней Греции, является актуальной и для больших размерностей из-за ее связи с задачами кодирования.

Начиная с работы великого К. Ф. Гаусса вплоть до нашего времени плотнейшие решетчатые упаковки были найдены только для размерностей d ≤ 8 и d = 24.

К сожалению, методы нахождения плотнейших упаковок в пространствах малых размерностей перестают «работать» для больших размерностей. Интуиция, выработанная в трехмерном пространстве, оказывается бессильной по отношению к этой задаче для пространств больших размерностей. Искренне удивляет, насколько сильно максимальная плотность упаковки пространства шаров убывает в зависимости от размерности пространства. Так, на плоскости максимальная плотность упаковки кругов равна 0,9069... В трехмерном пространстве максимальная плотность упаковки шаров равна 0,7404..., в 8-мерном — 0,2536... В 24-мерном пространстве максимальная плотность упаковки — только 0,0019...! Другими словами, никакая упаковка 24-мерных шаров не может занимать даже 0,2% пространства!

Работа Вороного об упаковках шаров

Вороному удалось создать метод нахождения плотнейшей решетчатой упаковки d-мерного пространства равными шарами для любой размерности.

Для этого Вороной рассмотрел конус ПКФ, состоящий из точек, представляющих положительные квадратичные формы от d переменных. Размерность этого конуса равна числу коэффициентов \( \frac{d(d + 1)}{2} \) в квадратичной форме.

Среди форм конуса Вороной выделил совершенные формы. Совершенная форма — это ПКФ, имеющая столь много арифметических минимумов, что ее коэффициенты задаются координатами (x, y) этих минимумов однозначно (с точностью до общего множителя).

Например, форма f₁(x, y) = x² + y² имеет две пары арифметических минимумов ±(1, 0) и ±(0, 1) и не является совершенной. Форма f₂(x, y) = x² + xy + y² имеет три пары арифметических минимумов ±(1, 0), ±(0, 1) и ±(−1, 1). По этим трем парам форма f₂(x, y) определяется однозначно (с точностью до общего множителя), т.е. форма f₂(x, y) является совершенной.

Вороной получил для совершенных форм три результата. Во-первых, он доказал, что форма, отвечающая плотнейшей упаковке, является совершенной. Во-вторых, он установил, что совершенных форм от данного числа переменных — конечное число. И самое главное, в-третьих, Вороной предложил метод нахождения всех совершенных форм. Этот метод опирается на так называемый совершенный полиэдр, весьма сложный многомерный многогранник, введенный Вороным. В принципе, найдя методом Вороного все совершенные формы, можно вычислить плотности для конечного числа соответствующих упаковок и выделить те, которые отвечают максимальному значению.

Хотя применение метода Вороного для больших размерностей связано с огромными вычислениями, которые трудно реализовать даже на современных вычислительных машинах, метод Вороного был и остается единственным методом решения этой задачи, который годится для пространств любой размерности.

Параллелоэдры

Последний мемуар Вороного, как было сказано, посвящен теории параллелоэдров. Параллелоэдр — это выпуклый многогранник, копиями которого, прикладываемыми друг к другу по целым граням, можно заполнить пространство без пропусков и попарных перекрытий; при этом предполагается, что параллелоэдры не только конгруэнтны, но и параллельны друг другу, т.е. получаются друг из друга параллельными переносами.

В силу параллельности многогранников друг другу и их прилегания по целым граням, каждая грань параллелоэдра имеет равную и параллельную ей противоположную грань. Отсюда и название параллелоэдр, т.е. параллелогранник, которое дал им великий кристаллограф Евграф Степанович Федоров (1857–1919). Федоров начал изучать параллелоэдры в 1885 году из-за их значимости в кристаллографии. Действительно, разбиение пространства на параллелоэдры хорошо моделирует структуру кристалла, которая, как известно, периодическая в трех измерениях.

Двумерный аналог параллелоэдров называют параллелогоном. Параллелогон — это выпуклый многоугольник, параллельными копиями которого можно замостить плоскость, прилагая их друг к другу по целым сторонам. Поэтому параллелогон — это многоугольник с четным числом сторон, у которого каждая сторона имеет равную и параллельную пару.

Параллелогон, как легко показать, является центрально-симметричным многоугольником с четырьмя сторонами (т.е. параллелограммом) или с шестью сторонами. Легко видеть, что верно и обратное: любой центрально-симметричный многоугольник одного из этих двух типов (четырехугольник или шестиугольник) является параллелогоном.

Рис. 5

Все типы трехмерных параллелоэдров, а их оказалось пять, были найдены Федоровым (рис. 5; см. также «Калейдоскоп «Кванта»). На рисунке 5 фигура I — куб, II — шестиугольная призма, III — ромбододекаэдр, IV — вытянутый додекаэдр, V — усеченный октаэдр. На самом деле, точнее было бы говорить здесь не о пяти параллелоэдрах, а о пяти комбинаторных типах параллелоэдров. Как показали российские математики А. Д. Александров (1912–1999) и Б. А. Венков (1900–1964), каждый тип помимо указанного параллелоэдра содержит многогранники, устроенные точно так же, как и указанный представитель, у которых, подчеркнем, все грани центрально-симметричны.

Это означает, например, что в тип I помимо куба входят также и все параллелепипеды. А в тип II входят все призмы с центрально-симметричными шестиугольными основаниями и боковыми гранями-параллелограммами.

При выводе всех пяти типов параллелоэдров Федоров предполагал, что параллелоэдр — обязательно центрально-симметричный. Несмотря на имевшиеся аргументы в пользу этого предположения, строгого доказательства у Федорова не было. В отличие от двухмерного случая, доказательство центральной симметричности трехмерного параллелоэдра не так просто.

Г. Минковский после работы Федорова о параллелоэдрах заинтересовался этим классом многогранников, причем произвольной размерности. Попытка доказать центральную симметричность параллелоэдра привела Минковского к открытию одной из самых прекрасных теорем в теории выпуклых многогранников — теоремы о существовании и единственности выпуклого многогранника с данными направлениями граней и их площадями. Из этой сложно доказываемой теоремы Минковский легко вывел следующие первые два свойства параллелоэдров, к которым позже было добавлено третье (Б. Н. Делоне):

1. параллелоэдр — центрально-симметричный многогранник;
2. все грани параллелоэдра — центрально-симметричные многоугольники;
3. проекция параллелоэдра вдоль любого его ребра на перпендикулярную к нему плоскость есть либо параллелограмм, либо центрально-симметричный шестиугольник.

Причем все три свойства верны для параллелоэдров любой размерности. Разумеется, для параллелоэдров размерности d ≥ 4 свойства 2) и 3) должны быть отредактированы. Так, в условии 2) должно быть: «все грани размерности d − 1 — центрально-симметричные многогранники»; а в условии 3) речь должна идти о проекции параллелоэдра вдоль любой его (d − 2)-мерной грани на перпендикулярную к ней плоскость.

Значительно позже, в 1954 году, Б. А. Венков доказал, что эти три условия являются не только необходимыми, но и достаточными: любой выпуклый многогранник, удовлетворяющий условиям 1)–3), является параллелоэдром.

Параллелоэдры Вороного

Как устроены параллелоэдры в пространствах произвольной размерности? Как найти все параллелоэдры, точнее все комбинаторные типы параллелоэдров?

Именно этой проблеме был посвящен последний мемуар Вороного. В нем Георгий Феодосьевич построил теорию параллелоэдров особого вида, называемых теперь параллелоэдрами Вороного.

Рис. 6

Пусть Λ — произвольная решетка (рис. 6, а). Областью Вороного данной точки А в решетке Λ называется множество V_A всех точек Х плоскости, которые находятся от точки A ∈ Λ не дальше, чем от остальных точек В решетки Λ:

|XA| ≤ |XB| для всех B ∈ Λ, B ≠ A.

Для того чтобы построить область Вороного, в принципе нужно соединить данную точку А с каждой точкой B ∈ Λ и провести срединный перпендикуляр к отрезку [AB]. Срединный перпендикуляр делит плоскость на две полуплоскости. Полуплоскость, содержащая точку A, состоит из тех точек X плоскости, которые расположены к А ближе, чем к В. Та часть плоскости, которая принадлежит всем таким полуплоскостям (пересечение полуплоскостей), и есть область Вороного для точки А.

Согласно определению, область Вороного есть пересечение бесконечного числа полуплоскостей. В действительности же в построении области Вороного участвуют лишь конечное число срединных перпендикуляров, соответствующих относительно близким к A точкам В из Λ. Другими словами, область Вороного V_A есть выпуклый многоугольник, образованный несколькими срединными перпендикулярами. Если построить теперь область Вороного V_B для каждой точки В решетки Λ, то очевидно получим равные и параллельные друг другу многоугольники, которые заполняют плоскость без пропусков и перекрытий (рис. 6, б).

Таким образом, согласно определению, область Вороного точки для решетки на плоскости есть параллелогон. Совершенно аналогично, для решетки в пространстве область Вороного есть трехмерный многогранник — параллелоэдр, называемый в наше время параллелоэдром Вороного.

Надо сказать, что идея области Вороного для дискретных множеств восходит к временам Декарта (1596–1650). В XIX веке концепцию области Вороного в двумерном случае активно использовал знаменитый немецкий математик Дирихле и на протяжении более века эти области назывались областями Дирихле. Но самые глубокие результаты об этих областях, причем для произвольной размерности, были получены Г. Ф. Вороным, и в настоящее время эти области называют в его честь.

Невозможно в рамках статьи описать теорию параллелоэдров, построенную Вороным. Скажем, что она, в частности, содержит метод нахождения всех типов параллелоэдров Вороного для любой размерности. Как соотносится решение этой более узкой задачи к задаче нахождения типов всех параллелоэдров вообще?

Дело в том, что не каждый параллелоэдр является параллелоэдром Вороного. Так, среди параллелограммов только прямоугольники являются областями Вороного (рис. 7, а). Центрально-симметричный шестиугольник является областью Вороного тогда и только тогда, когда он вписан в окружность (рис. 7, б). Тем не менее, для пространств размерности d = 2, 3 и 4 найдены все типы параллелоэдров. Число типов для этих размерностей равно 2, 5 и 52 соответственно, причем установлено, что каждый из этих типов может быть реализован как область Вороного.

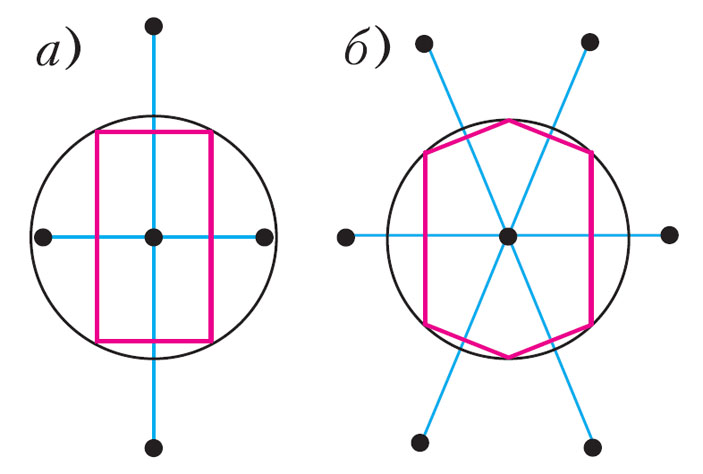
Рис. 7

Георгий Феодосьевич предположил, что это верно для параллелоэдров любой размерности d, т.е. любой параллелоэдр размерности d устроен так же, как некоторый параллелоэдр Вороного.

Для тех, кто знаком с понятием аффинного преобразования, уточним смысл гипотезы Вороного: для всякого параллелоэдра существует аффинное преобразование, которое переводит этот параллелоэдр в некоторый параллелоэдр Вороного.

Если гипотеза подтвердится, то метод Вороного, при помощи которого можно перечислить все типы параллелоэдров Вороного, решает также вопрос и о перечислении типов всех параллелоэдров вообще. Если же гипотеза Вороного неверна, то общая проблема описания всех параллелоэдров остается открытой.

Этой гипотезе посвящена значительная часть мемуара Вороного. В частности, в нем Вороной доказал гипотезу для очень важного класса параллелоэдров, так называемых примитивных.

Однако, несмотря на усилия многих математиков, проблема остается нерешенной на протяжении века для всех размерностей d ≥ 5. Загадочное на первый взгляд упоминание в «Калейдоскопе «Кванта» о «не менее 110244» типах пятимерных параллелоэдров означает, что, с одной стороны, найдены все 110244 типа пятимерных параллелоэдров Вороного. А с другой стороны, всех типов может быть и больше, так как не известно, есть ли еще какие-либо пятимерные параллелоэдры иного строения.

На пути решения проблемы Вороной предложил совершенно замечательную конструкцию — так называемый «подъем диаграммы Вороного на параболоид».

Пусть \( \mathscr{X} \) — дискретное множество точек на плоскости (x, y) и нам нужно построить «диаграмму Вороного», т.е. сетку из областей Вороного относительно этих точек. Рассмотрим функцию z(x, y) = x² + y².

Ее графиком будет поверхность — параболоид вращения, который получается вращением параболы вокруг своей оси. «Поднимем» каждую точку X из \( \mathscr{X} \) на параболоид. Проведем в каждой «поднятой» точке X′ плоскость, касательную к параболоиду. Касательные плоскости вырезают многогранник, описанный около параболоида (рис. 8). Вороной заметил, что если спроектировать этот многогранник на плоскость, то проекции граней совпадают с областями Вороного. Тем самым, задача построения диаграммы Вороного для данного множества сводится к построению выпуклого многогранника. Этот подход широко используется в современной вычислительной геометрии и компьютерной графике.

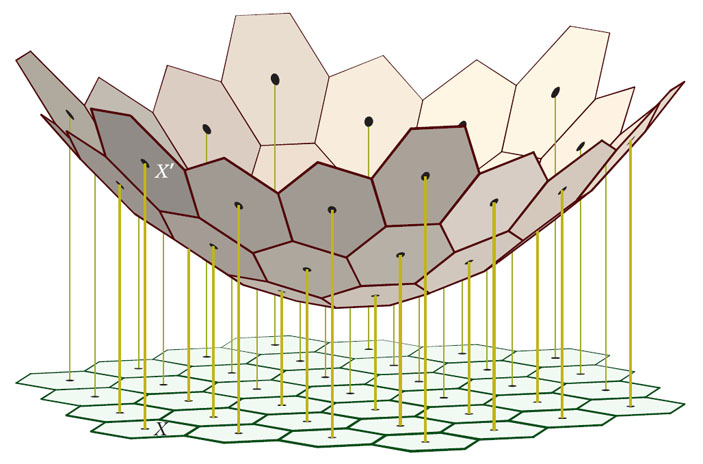
Рис. 8. Рисунок Я. Кучериненко

Заметим, что диаграмма Вороного тесно связана с другой важной сеткой — разбиением Делоне (рис. 9). Напомним, что разбиение Делоне плоскости также однозначно задается множеством \( \mathscr{X} \) (см. статью «Многогранный Делоне» в «Кванте» №1, 2 за 2010 г.). Между диаграммой Вороного и разбиением Делоне имеется соответствие дуальности:

• каждой области Вороного V_A соответствует вершина разбиения Делоне, которая является центром А этой области;
• ребру е диаграммы Вороного, разделяющему области V_A и V_B, соответствует ребро АВ в разбиении Делоне;
• вершине v в диаграмме Вороного соответствует ячейка Делоне, вершины которой суть центры областей Вороного, сходящихся в v.

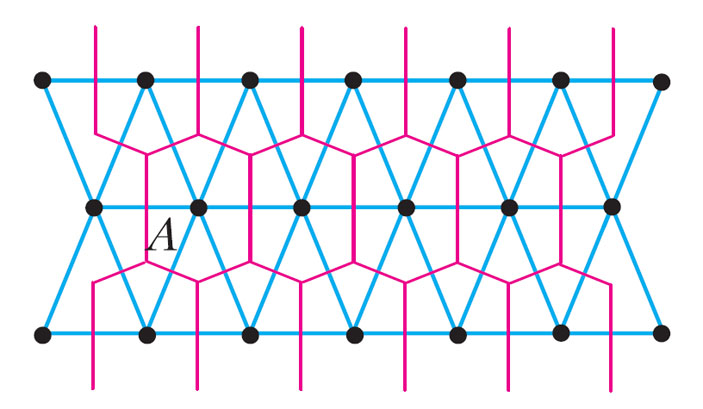
Рис. 9

Заключая очерк об одном из самых крупных математиков, когда-либо работавших в теории чисел, подчеркнем, что глубокие идеи Георгия Феодосьевича Вороного не только оказывают влияние на современную теорию чисел, но и играют большую роль во многих науках и приложениях.