Игрушки на елку: разгадки

Александр Бердников, Георгий Челноков
«Квантик» №2, 2019

В прошлом номере игрушки на новогодней ёлке подсказали Квантику несколько интересных задач:

• Нарисуйте многоугольник, у которого каждая сторона лежит на одной прямой ровно с одной другой стороной. Может ли каждая сторона лежать на одной прямой ровно с двумя другими сторонами? А ровно с 10 другими?
• Существует ли многогранник, у которого каждая грань лежит в одной плоскости ещё ровно с одной другой гранью? Бывает ли, что каждая грань лежит в одной плоскости с двумя другими гранями, или даже с 10 другими?

Некоторые ответы и правда можно найти среди новогодних украшений. Например, плоская пятиугольная звёздочка на вершине ёлки — это многоугольник, каждая сторона которого содержит ровно одну другую в своём продолжении (рис. 1).

Рис. 1 (слева) и 2

Обычно эту звёздочку делают объёмной — как раз в виде многогранника, грани которого разбиваются на пары лежащих в одной плоскости. На рисунке 2 эти пары окрашены в один цвет (показана только «верхняя» половина объёмной звезды, обратная сторона устроена так же).

Рис. 3 (слева) и 4

А что насчёт трёх (и более) сторон на прямой? У звёздочек с большим числом лучей стороны (и грани) снова разбиваются лишь на пары (рис. 3 и 4). Зато внутри многоугольника появилось много отрезков, лежащих на тех же прямых, что и стороны. Вот бы часть из них сделать сторонами... Конечно — вырежем внутреннюю часть, как на следующих двух рисунках. Получим многоугольники, у которых стороны лежат на прямых по три (рис. 5) и по четыре (рис. 6).

Рис. 5 (слева) и 6

Но это многоугольники с дырками, и неясно, как дальше увеличивать число сторон на одной прямой.

Обратим внимание на симметричный узор из множества частей, образованный проведёнными линиями. Идея: давайте наоборот, не вырезая центральную часть, уберём какие-то другие части узора, чтобы от центра к краям шли отростки, поворачивая то вправо, то влево. Так, на рисунке 7 стороны разбиваются на пятёрки лежащих на одной прямой.

Рис. 7

Чем больше отростков и чем больше поворотов они сделают, тем больше сторон попадут на одну прямую.

Приведём ещё два хитрых примера, где наклон линий узора немного изменён, так что на одну прямую попадают только стороны из двух соседних отростков (в первом случае) и из трёх соседних (во втором). В итоге в первом примере (рис. 8) стороны лежат на одной прямой по три, а во втором (рис. 10) — по четыре.

Рис. 8

Идея тут такая. Легко нарисовать по клеткам периодическую ломаную со сколь угодно большим числом сторон, у которой каждая сторона лежит на одной прямой ровно с n другими (рис. 9 — пример для n = 3).

Рис. 9

Замкнём длинную полоску с этой ломаной в кольцо, растягивая в плоскости так, чтобы стороны меняли свою длину, но по-прежнему лежали на прямых. Загибая полоску, каждую очередную прямую (содержащую стороны) мы повернём совсем немного, и внутренность итоговой ломаной даст нужный многоугольник. Так, рисунок 10 получен из полоски с рисунка 9.

Рис. 10

Попробуйте сами построить картинки для большего числа сторон на одной прямой. А может быть, вы придумаете совсем другие примеры — скажем, построите нужные многоугольники «по клеточкам»? Тогда обязательно пришлите их нам в редакцию!

Из решения на плоскости получается пространственное тем же способом, как из плоской звёздочки получается объёмная звезда: надо склеить две пирамиды, общее основание которых — наш многоугольник. К сожалению, такой многогранник с виду мало отличается от звезды, так как всё интересное у него запрятано глубоко внутри...

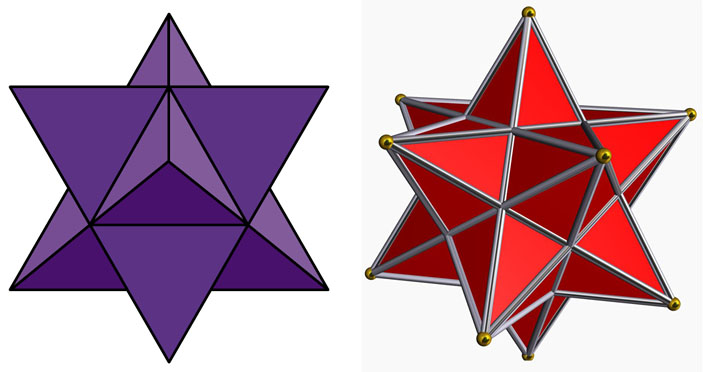
Рис. 11 (слева) и 12

А вот два многогранника попроще — звёздчатый октаэдр (рис. 11) и звёздчатый додекаэдр (рис. 12). Отчётливо видно, что у первого грани разбиваются на тройки лежащих в одной плоскости, а у второго — на пятёрки.

Художник Анна Горлач