Замощения параллелоэдрами
Алексей Гарбер
«Квант» №1, 2019

Несложно показать, что копиями любого треугольника и любого четырехугольника (даже невыпуклого) можно замостить плоскость (см. верхний ряд рисунков). Сложнее показать, что ни одним выпуклым многоугольником с семью и более сторонами нельзя замостить плоскость и что только три семейства выпуклых шестиугольников допускают такое замощение. Самый сложный случай — пятиугольники. К концу XX века было найдено 14 семейств выпуклых пятиугольников, замощающих плоскость, еще одно, 15-е семейство обнаружено в 2015 году (см. «Калейдоскоп „Кванта“» №5 за 2017 г.); а доказательства, что это все семейства, до сих пор нет.
Для многих выпуклых многоугольников, которыми можно замостить плоскость, необходимо, чтобы некоторые их копии были повернуты или отражены относительно некоторой прямой. Исключениями являются параллелограммы и центрально-симметричные шестиугольники; ими можно замостить плоскость, используя только параллельные переносы (см. нижний ряд рисунков).
В произвольной размерности выпуклый многогранник, копиями которого можно заполнить все пространство, используя только параллельные переносы, называется параллелоэдром. Таким образом, существует всего два семейства двумерных параллелоэдров — параллелограммы и центрально-симметричные шестиугольники. В трехмерном пространстве параллелоэдры были классифицированы Е. Федоровым в 1885 году. Существует пять семейств трехмерных параллелоэдров с разными комбинаторными типами. Наиболее «правильные» представители семейств — куб, правильная шестиугольная призма с равными ребрами, ромбододекаэдр, удлиненный ромбододекаэдр, усеченный октаэдр (см. рисунки внизу). Все остальные получаются из них аффинными преобразованиями, а также операциями «удлинения» параллельных ребер.
С ростом размерности число семейств растет очень быстро. Если в четырехмерном пространстве ровно 52 семейства параллелоэдров, то в более высоких размерностях даже точное их количество неизвестно. Известно лишь, что в пятимерном пространстве существует не менее 110 244 различных семейств параллелоэдров, а в шестимерном — не менее полумиллиарда.
Внизу изображены также развертки всех пяти трехмерных параллелоэдров. Сможете ли вы собрать соответствующие замощения для каждого из них?
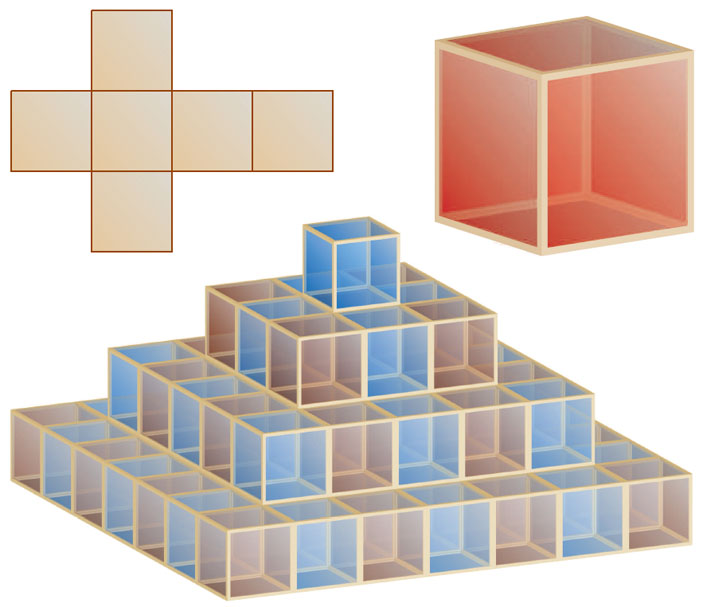

Правильная шестиугольная призма с равными ребрами

Ромбододекаэдр (угол ромба arccos 1/3)
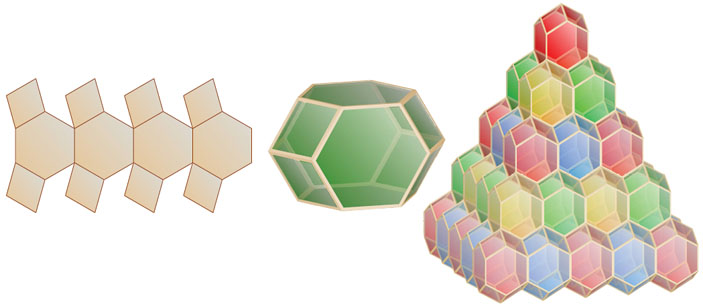
Удлиненный ромбододекаэдр (угол ромба arccos 1/4)
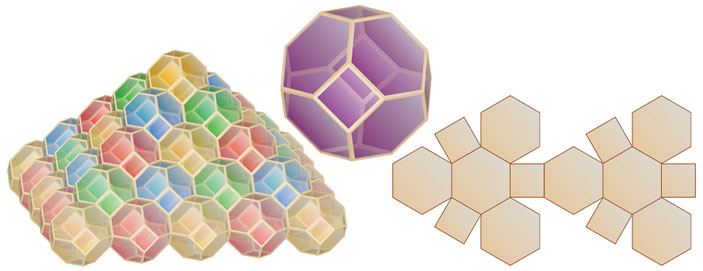
Усеченный октаэдр
Рисунки М. Панова
Мозаики и замощения
-
 30.07.2025Апериодическая плиткаХайдар Нурлигареев • Библиотека • «Квантик» №11, 2024
30.07.2025Апериодическая плиткаХайдар Нурлигареев • Библиотека • «Квантик» №11, 2024
-
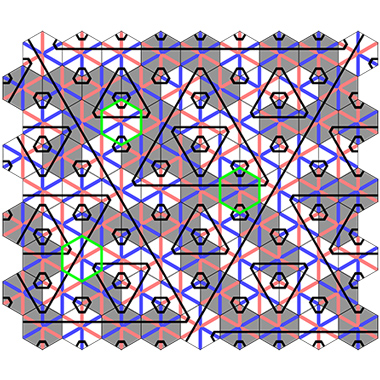 28.04.2023Замощение Соколара — ТейлорМихаил Грунтов, Хайдар Нурлигареев • Картинки дня
28.04.2023Замощение Соколара — ТейлорМихаил Грунтов, Хайдар Нурлигареев • Картинки дня
-
 28.04.2023Решена «задача Эйнштейна» о замощении плоскостиХайдар Нурлигареев • Новости науки
28.04.2023Решена «задача Эйнштейна» о замощении плоскостиХайдар Нурлигареев • Новости науки
-
 29.08.2021Теорема Наполеона, замощения плоскости и параллельникиГригорий Мерзон • Библиотека • «Квантик» №12, 2020
29.08.2021Теорема Наполеона, замощения плоскости и параллельникиГригорий Мерзон • Библиотека • «Квантик» №12, 2020
-
 21.07.2021Замощения параллелоэдрамиАлексей Гарбер • Библиотека • «Квант» №1, 2019
21.07.2021Замощения параллелоэдрамиАлексей Гарбер • Библиотека • «Квант» №1, 2019
-
 03.06.2021Мозаика РобинсонаХайдар Нурлигареев • Библиотека • «Квантик» №10, 2020
03.06.2021Мозаика РобинсонаХайдар Нурлигареев • Библиотека • «Квантик» №10, 2020
-
 30.05.2021Оклейка тетраэдра шестиугольникамиНиколай Авилов • Библиотека • «Квант» №10, 2018
30.05.2021Оклейка тетраэдра шестиугольникамиНиколай Авилов • Библиотека • «Квант» №10, 2018
-
 06.12.2020Как разрезать верблюда?Григорий Мерзон • Библиотека • «Квантик» №5, 2020
06.12.2020Как разрезать верблюда?Григорий Мерзон • Библиотека • «Квантик» №5, 2020
-
 03.06.2020Плитки и числа ХеешаХайдар Нурлигареев • Библиотека • «Квантик» №10, 2019
03.06.2020Плитки и числа ХеешаХайдар Нурлигареев • Библиотека • «Квантик» №10, 2019
-
 09.08.2019Ковер СерпинскогоХайдар Нурлигареев • Картинки дня
09.08.2019Ковер СерпинскогоХайдар Нурлигареев • Картинки дня













Куб