Треугольная формула Пика

Игорь Акулич
«Квантик» №8, 2021

Знаменитая формула Пика получила своё название по имени автора — австрийского учёного Георга Александра Пика, опубликовавшего её на рубеже XIX и XX веков. Формула Пика удивительно красива, и потому является любимой темой популярных публикаций (можно порекомендовать статью Г. Мерзона «Площадь многоугольников и тающий лед» из 9-го номера «Квантика» за 2018 год либо более раннюю статью Н. Васильева «Вокруг формулы Пика» из 12-го номера «Кванта» за 1974 год — в этих статьях приводится и её доказательство).

Поскольку, возможно, не все читатели в курсе дела, вкратце изложим суть. Пусть бесконечная плоскость разбита вертикальными и горизонтальными прямыми на одинаковые квадраты, площадь каждого из которых равна s₀ (обычно для простоты принимают s₀ = 1, но нам здесь удобнее именно так — в общем виде). Назовём узлами точки, являющиеся вершинами квадратов, и нарисуем произвольный многоугольник, все вершины которого лежат в узлах. При этом стороны многоугольника не обязаны быть вертикальными или горизонтальными (хотя это и не возбраняется). Например, у пятиугольника на рисунке 1 только одна сторона горизонтальна, а остальные — наклонны.

Рис. 1

Подсчитаем количество узлов, попавших строго внутрь многоугольника (на рисунке 1 они выделены красным цветом), а также количество узлов, оказавшихся на границе многоугольника. Заметим, что на границе находятся, во-первых, все вершины многоугольника (синие), а также те узлы, что волею случая оказались на сторонах (зелёные). В частности, у нашего пятиугольника имеется 39 красных узлов, а синих, разумеется, 5 (в каждой вершине), и плюс ещё 12 зелёных на сторонах. Итого на границе 5 + 12 = 17 узлов.

Георг Пик доказал, что площадь S любого такого многоугольника зависит только от количества вершин каждого типа, то есть S есть функция от числа вершин В, лежащих внутри многоугольника, и от числа вершин Г, попавших на границу, и эту функцию можно записать в виде формулы (её-то и называют формулой Пика):

S (В, Г) = (В + 0,5 Г – 1) · s₀.

Вернувшись к тому же пятиугольнику на рисунке 1, мы без труда найдём его площадь. Здесь В = 39, Г = 17, и потому площадь равна S (39, 17) = (39 + 0,5 · 17 – 1) · s₀ = 46,5 · s₀. А попробуйте-ка подсчитать «вручную»!¹

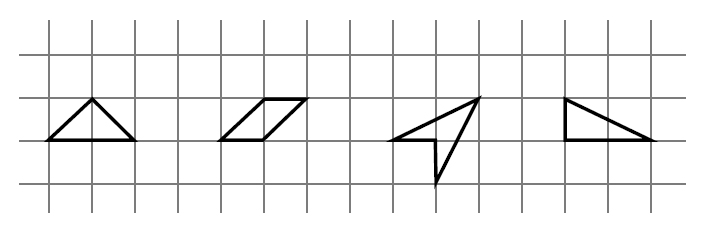
Рис. 2

Сила формулы Пика ещё и в том, что форма многоугольника, оказывается, в каком-то смысле «вторична», главное — количество тех или иных узлов. Например, на рисунке 2 изображены несколько разных многоугольников, но у них всех В = 0 и Г = 4, потому площади их одинаковы (кстати, чему они равны?).

Формула Пика столь изящна, что не хочется верить, будто она работает только для квадратной решётки. И действительно, формула Пика применима для любой бесконечной сетки, состоящей из равных параллелограммов, и внешне выглядит точно так же (если площадь «элементарного» параллелограмма равна s₀). То есть все «растяжки» и «перекосы», превращающие квадрат в параллелограмм, ничуть не сказываются на её справедливости.

Но и это далеко не всё. С не меньшим успехом можно разбить плоскость прямыми трёх направлений (под углами 60° друг к другу) на одинаковые треугольники (рис. 3). Представим себе многоугольник, вершины которого лежат в узлах этой треугольной решётки, и зададимся вопросом: не будет ли площадь S этакого многоугольника тоже зависеть только от количества узлов, попавших внутрь (В) и на границу (Г) многоугольника, и если да — то какова эта зависимость S (В, Г)? Площадь каждого из «элементарных» треугольников, на которые разбита плоскость, мы считаем равной s₀. Иными словами, существует ли для такой сетки аналог формулы Пика (которую уместно назвать треугольной формулой Пика)?

Рис. 3

Оказывается, да! Чтобы в этом убедиться, сначала у сетки, изображённой на рисунке 3, удалим все прямые одного из трёх направлений (например, идущие с «северо-запада» на «юго-восток»). Получится «ромбическая» сетка, где каждый ромб образован объединением двух треугольников (рис. 4), и потому площадь такого «элементарного» ромба равна 2 s₀. Вместе с тем, после удаления всех прямых одного направления ни один узел не пропал — просто теперь в каждом узле пересекаются не три, а две прямые. И если на сетке был нарисован многоугольник с вершинами в узлах, то его граница будет проходить через столько же узлов, сколько и ранее, да и количество узлов внутри многоугольника не изменится.

Рис. 4

А поскольку ромб — частный случай параллелограмма, для указанной сетки можно применить формулу Пика (помня, что площадь элементарного ромба равна не s₀, а 2 s₀). Разумеется, она же окажется верной и для исходной треугольной сетки. Итак, для треугольной сетки площадь многоугольника с вершинами в узлах сетки находится по формуле:

S_треуг. (В, Г) = (В + 0,5 Г – 1) · 2 s₀ = (2 В + Г – 2) · s₀.

Рис. 5

Можно двинуться и дальше. Рассмотрим сетку, напоминающую кирпичную кладку (рис. 5), на которой одинаковые «прямоугольники-кирпичи» образуют полосы, сдвинутые на «полкирпича» относительно соседней полосы. Не поискать ли для неё аналог формулы Пика? Здесь, разумеется, узлами считаем все точки, являющиеся вершинами какого-либо элементарного прямоугольника, площадь которого, по традиции, примем равной s₀.

К счастью, и здесь успех гарантирован. Надо всего лишь каждый прямоугольник разбить по вертикали на два «полукирпича». В результате получится «типовая» сетка из прямоугольников, образуемых двумя семействами прямых, для которой формула Пика очень даже применима. Надо лишь учесть, что здесь (в противоположность рассмотренной выше треугольной сетке) элементарный прямоугольник будет вдвое меньше исходного, и потому его площадь равна 0,5 s₀. Поэтому для «кирпичной» сетки формула Пика такова:

S_кирп. (В, Г) = (В + 0,5 Г – 1) · 0,5 s₀ = (0,5 В + 0,25 Г – 0,5) · s₀.

А сейчас предлагаем читателю самостоятельно найти аналог формулы Пика для сетки, состоящей из равных прямоугольных треугольников. Она получается из обычной квадратной сетки, если каждый её квадрат обеими диагоналями разрезать на четыре равные части (рис. 6). Разумеется, здесь s₀ — площадь каждого прямоугольного треугольника, на которые разделена плоскость. А потом сверьтесь с ответом.

Рис. 6

Ответ

В разбиении плоскости на прямоугольные треугольники уберём все горизонтальные и вертикальные прямые. Получится квадратная сетка, образованная пересекающимися наклонными прямыми, в ней каждый квадрат «склеен» из двух прямоугольных треугольников (и «пропавших» узлов нет!). Площадь такого квадрата равна 2 s₀, и потому формула Пика выглядит точь-в-точь как для сетки из правильных треугольников:

S (В, Г) = (В + 0,5 Г – 1) ·2 s₀ = (2 В + Г – 2) · s₀.

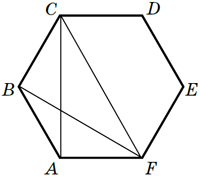
А для шестиугольной сетки аналога формулы Пика нет! Чтобы в этом убедиться, рассмотрим одну шестиугольную ячейку ABCDEF сетки (рисунок справа). Сравним треугольники ABF и ACF. У них основание AF — общее, но третьи вершины (B и C) находятся на разных расстояниях от прямой AF. Тогда площади их заведомо различны. С другой стороны, количества точек, попавших на границу и внутрь каждого треугольника, одинаковы: Г = 3, В = 0. Поэтому аналог формулы Пика (если бы он существовал) дал бы одинаковые значения их площадей. Противоречие!

В заключение вспомним, что плоскость можно разделить не только на равные квадраты и треугольники, но и на шестиугольники — наподобие пчелиных сот (рис. 7). Может, и для такой сетки существует аналог формулы Пика? Попробуйте это выяснить.

Рис. 7

Существуют, кстати, обобщения формулы Пика для определения объёмов тел в трёхмерном пространстве (и даже в пространствах более высоких размерностей) — так называемый многочлен Эрхарта. Но это очень сложная тема, уводящая слишком далеко. Поэтому углубляться не будем.

Художник Алексей Вайнер

¹ Конечно, тоже не ахти какая сложность — надо лишь разбить многоугольник на прямоугольники и прямоугольные треугольники, но повозиться придётся всё-таки дольше.