Магические квадраты Ло Шу и Кхаджурахо

Фёдор Нилов
«Квантик» №7, 2022

Древний китайский магический квадрат Ло Шу представляет собой таблицу 3 × 3, заполненную цифрами от 1 до 9 так, что сумма цифр в каждой строке, каждом столбце и обеих диагоналях одна и та же. Попробуйте составить такой квадрат самостоятельно, не подглядывая на картинку справа (каждая цифра равна числу точек). Бытует легенда, что примерно в 2200 году до н.э. китайский император обнаружил эти точки на ячейках панциря черепахи на берегу реки Хуанхэ.

Поясним, как можно построить квадрат Ло Шу алгоритмически, не перебирая варианты. Для начала поймём, чему равна эта постоянная сумма, называемая магической константой.

Сумма всех чисел в таблице равна 1 + 2 + ... + 9 = 45. Тогда сумма чисел в каждой строке в три раза меньше: 45/3 = 15. Заметим, что центральная клетка участвует в четырёх суммах (строка, столбец и две диагонали), угловая — в трёх суммах (строка, столбец и одна диагональ), а каждая из оставшихся боковых — в двух суммах (строка и столбец).

Где может стоять самое большое число, то есть 9? Мы должны дополнить 9 до 15 двумя различными слагаемыми. Это можно сделать лишь двумя способами: 1 + 5 и 2 + 4. Значит, 9 может находиться только в боковой клетке. Будем считать, что это верхняя боковая клетка. А сколько способов дополнить самое маленькое число 1? Тоже два: 9 + 5 и 8 + 6. Значит, 1 также стоит в боковой клетке, причём в нижней (ведь 1 и 9 входят в одну сумму). Тогда по центру автоматически стоит 5. В одной горизонтали с 9 стоят числа 2 и 4, пусть 2 слева, а 4 — справа. Далее квадрат заполняется однозначно.

Возможно, вы слышали про магический квадрат 4 × 4, его изобразил немецкий художник Альбрехт Дюрер на своей гравюре «Меланхолия». В этом квадрате расставлены числа от 1 до 16 так, что суммы чисел во всех строках, столбцах, двух диагоналях и четырёх «угловых» квадратах 2 × 2 равны одной и той же магической константе; а ещё одинаковы суммы любых двух чисел, симметричных относительно центра. Кроме того, в нижней строке можно прочитать 1514 — год создания гравюры.

Квадрат Дюрера

В храме Святого Семейства в Барселоне, построенном по проекту Антонио Гауди, есть почти магический квадрат, очень похожий на квадрат Дюрера (правда, в нём некоторые числа повторяются), в этом квадрате магическая константа равна 33, возрасту Иисуса. Отметим, что среди людей, интересовавшихся магическими квадратами, были как известные математики, такие как Леонард Эйлер, Артур Кэли, так и любители, например Бенджамин Франклин.

Квадрат в храме Святого Семейства в Барселоне

На плите храма в древнем индийском городе Кхаджурахо, датируемой XI веком н.э., был обнаружен ещё более удивительный магический квадрат, его называют дьявольским.

Квадрат в храме Паршванатха в городе Кхаджурахо

Диагонали и пандиагонали

В клетках этого квадрата расставлены числа от 1 до 16 так, что одинаковы суммы во всех строках, столбцах, во всех девяти квадратах 2 × 2, двух диагоналях, а  также всех ломаных диагоналях, называемых пандиагоналями (каждая такая диагональ состоит из четырёх клеток одного цвета на рисунке справа).

Как же можно составить такой квадрат? Для начала поймём, чему равны все эти суммы. Если сложить числа в четырёх строках, получится сумма чисел от 1 до 16, то есть 136. Значит, сумма в одной строке равна 136 : 4 = 34, это и есть магическая константа.

Второе соображение — рассматривать пары «противоположных» чисел 1 и 16, 2 и 15 и т. п. Куда их стоит поставить? Наверное, в «противоположные» клетки, но какие клетки считать противоположными? Чтобы это понять, сделаем из квадрата «бублик»: сначала склеим две противоположные стороны так, чтобы получился цилиндр, а потом склеим две противоположные окружности цилиндра так, чтобы получился бублик или на математическом языке — тор.

Склейка тора из квадрата

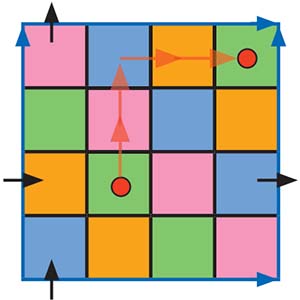
Прогулки по тору

Теперь у нашего магического квадрата нет края. Например, если мы стоим в левом верхнем углу и идём вверх, мы попадаем в левый нижний угол. Если стоим в синей клетке над правым нижним углом и идём вправо, попадаем в оранжевую клетку над левым нижним углом. Заметим, что на торе все строки, столбцы, диагонали и пандиагонали «замыкаются», причём диагонали и пандиагонали выглядят одинаково. Кроме того, образуются новые квадраты 2 × 2 (всего их будет 16). Оказывается, сумма чисел в этих новых квадратах автоматически будет равна магической константе. При этом на торе становится ясно, какие клетки считать противоположными. Давайте стартуем из любой клетки (на рисунке она помечена красной точкой) и пойдём на две клетки в вертикальном направлении (на рисунке идём вверх) и на две клетки в горизонтальном (на рисунке идём вправо). Заметим, что конечная клетка не зависит от того, вправо или влево, вверх или вниз мы идём. Эта клетка — противоположный угол квадрата 3 × 3. Таким образом, все клетки разбились на пары противоположных (углов квадратов 3 × 3), в которые мы будем ставить противоположные числа. Сумма чисел в  каждой диагонали и пандиагонали равна сумме двух пар противоположных чисел, то есть 17 · 2 = 34, магической константе. Осталось проследить за тем, чтобы сумма чисел в каждой строке, столбце и квадрате 2 × 2 была такой же. Давайте поместим в двух противоположных клетках числа 1 и 16.

Заметим, что в клетках рядом с числом 16 не могут стоять 15 и 14: оставшиеся два слагаемых в сумме должны были бы давать 3 и 4 соответственно, но тогда одно из них равно единице, а она уже стоит в другом месте. Аналогично 15 и 14 не могут стоять в одной строке или столбце с 16. Для перебора остаётся не так много вариантов.

Ответ

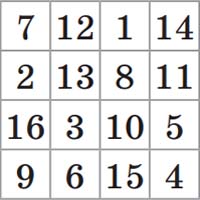
Легко опознать единицу: с неё начинаются двузначные числа. Цифры 0, 2 и 3 легко узнаваемы по виду. Из того, что сумма цифр в центральном квадрате 2 × 2 равна 34, находим цифру 8, и т.д.

Художник Алексей Вайнер