Магическая математика

Михаил Евдокимов
«Квантик» №12, 2019

Лёва усердно пытался решить задачи математического кружка, но задачи не поддавались. Пришлось просить помощи у отца.

— Ну, что вам тут задали? — спросил Олег Сергеевич. Он окончил мехмат МГУ и ему всё ещё казалось, что он с лёгкостью решит любую задачу... Уж за шестой-то класс точно!

— Вот, — Лёва протянул листок с условием, — тут три задачи. Учитель сказал, что это одна и та же задача, но я не понимаю, почему??? Мне они кажутся абсолютно разными!

— Хм, мне тоже так кажется... — Олег Сергеевич провёл рукой по некогда пышной шевелюре и задумался. — Если бы в третьей задаче речь шла не о произведениях, а о суммах, то её было бы легко решить. В математике это называется магическим квадратом. Магический квадрат 3 × 3, в котором записаны целые числа от 1 до 9, знали ещё в Древнем Китае более чем за 2000 лет до нашей эры! А ты сможешь заполнить клетки таблицы 3 × 3 числами от 1 до 9, чтобы суммы чисел в каждом столбце, каждой строке и на каждой из двух диагоналей были одинаковы?

— Папа, ты вместо того, чтобы помочь, задаёшь мне четвёртую задачу!? — возмутился Лёва.

— Подожди, возможно это необходимо... Давай решим её вместе! Какие у тебя идеи?

— Ну, чисел всего 9. Значит, можно попробовать перебрать варианты... — нерешительно произнёс Лёва.

— Не торопись. Смотри, в первую клетку таблицы можно записать целое число от 1 до 9, это 9 способов. В следующую выбираем уже из оставшихся, то есть 8-ю способами, и т. д. Получается, что всего способов 9 · 8 · 7 · 6 · 5 · 4 · 3 · 2 · 1. Мой смартфон показывает, что это число (математики его называют «9 факториал» и обозначают 9!) равно 362 880. Даже если проверять по таблице в секунду, на всю проверку уйдёт около 100 часов изнурительного однообразного труда. В общем, до следующего кружка не успеешь. Перебор можно подсократить за счёт одинаковых таблиц (отличающихся только поворотом или отражением), но это не тот путь, которым бы я советовал идти...

— Что же делать??? — перебил Лёва.

— Думай! Знаем ли мы что-то про такую таблицу?

— Ну, знаем, что в ней все числа от 1 до 9, но не знаем, как они там переставлены.... Ага, понял! Мы можем сказать, чему равна сумма чисел в строке или столбце. Так как общая сумма 1 + 2 + 3 +... + 9 равна 45, всего в таблице 3 столбца и в каждом сумма одинакова, то эта сумма должна равняться 45 : 3 = 15.

— Отлично! А можешь теперь сказать, какое число должно стоять в центре и почему?

— Не знаю...

Рис. 1

— Ну, давай подумаем вместе, — Олег Сергеевич нарисовал на листе квадрат и 4 стрелки. — Просуммируем числа в таблице по четырём направлениям, показанным стрелками на рисунке 1. По условию, должно получиться 4 раза по 15, то есть в сумме 60. С другой стороны, в общую сумму войдут все числа таблицы по одному разу, кроме центрального числа (обозначим его через x), оно войдёт 4 раза вместо одного. Но сумму всех чисел в таблице мы уже знаем, она равна 45. Получаем, что 60 = 45 + 3x. Значит, x = 5. То есть в центре может стоять только 5.

— Здорово! Выходит, мы можем сильно сократить перебор? — спросил Лёва.

— Всё ещё проще. Поставим куда-нибудь девятку. Например, так (рис. 2).

Рис. 2 (слева) и 3

Тогда вместо знака «?» стоит 1, ведь сумма чисел строки равна 15. Если в последнем столбце (там, где 1) не стоит 8, то сумма чисел в нём не больше 1 + 7 + 6 < 15, а должна быть равна 15. Итак, 8 стоит в одной из крайних клеток третьего столбца. Например, так (рис. 3).

Теперь вся таблица восстанавливается из того, что сумма чисел каждой строки, столбца или диагонали равна 15. Вот этот процесс по шагам (рис. 4).

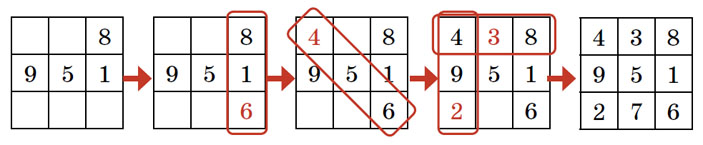
Рис. 4

Легко проверить, что такая таблица подходит.

— Но какая связь с нашими тремя задачами!?? Мы же просто решили задачу, которую нам не задавали! — казалось, что Лёва был расстроен.

Рис. 5

— Видимо, связь всё же есть! Давай начнём с третьей задачи. Условие того, что произведения чисел равны, легко заменить на условие, что суммы равны. Для этого просто берём, например, степени двойки: 2¹, 2², 2³, ... Ведь при произведении двух степеней их показатели складываются: 2^x · 2^y = 2^(x + y).

Поэтому, заменив каждое число магического квадрата на двойку в степени, равной этому числу, мы получим искомую таблицу (рис. 5). Задача решена!

— Хорошо, но третья задача хотя бы тоже про таблицу. А как связать это с первой задачей?

Рис. 6

— В ней же тоже есть набор из 9 чисел: от 100 до 900 с одинаковым шагом 100. Давай запишем их в виде магического квадрата с одинаковой суммой по строкам и столбцам, просто дописав нули к числам построенного магического квадрата (рис. 6).

Положим на первую чашку весов слитки, соответствующие числам первой строки, а на вторую — слитки, соответствующие числам второй строки (рис. 7). Если одна из чашек перевесила, то мы знаем набор из трёх слитков, в котором более лёгкий слиток. Если же весы в равновесии, то более лёгкий слиток в наборе последней строки. В любом случае, после первого взвешивания мы знаем строку таблицы, в наборе которой есть более лёгкий слиток.

Рис. 7 (слева) и 8

Далее кладём на первую чашку весов слитки, соответствующие числам первого столбца, а на вторую чашку — слитки, соответствующие числам второго (рис. 8). Аналогично, находим столбец с наиболее лёгким слитком, и сам этот слиток — он на пересечении найденных строки и столбца!

— Красиво! А как быть с борцами? Там же вообще нет никаких чисел!

Рис. 9

— Нет, значит их нужно ввести, — спокойно ответил Олег Сергеевич. Он только что понял, как нужно решать эту задачу. — Итак, у нас 9 борцов. Обозначим их силу числами от 1 до 9. Давай снова посмотрим на магический квадрат и отметим борцов, которые входят в наши команды (рис. 9).

Во встрече любых двух команд всего будет 9 поединков (можно образовать 3 × 3 = 9 разных пар соперников). Первая команда выиграет у второй со счётом 5 : 4, так как 2 > 1, 7 > 5, 7 > 1, 6 > 5, 6 > 1 (всего 5 побед из 9). Вторая команда выиграет у третьей со счётом 5 : 4, так как 9 > 4, 9 > 3, 9 > 8, 5 > 4, 5 > 3. И третья команда выиграет у первой со счётом 5 : 4, так как 4 > 2, 3 > 2, 8 > 2, 8 > 7, 8 > 6. Вот мы и разбили борцов на три команды как требовалось!

— Просто магия какая-то! — удивился Лёва.

— А математика это и есть магия, — загадочно улыбнулся Олег Сергеевич.

Художник Мария Усеинова