Магическое колесо

Как и в задачах с магическими квадратами, надо найти центральное число и сумму чисел на каждом отрезке.

Пусть суммы чисел, расположенных вдоль каждого отрезка равны S, а центральное число обозначим за х. Сумма всех чисел, как несложно подсчитать, равна 91. Сложив шесть сумм чисел, лежащих на прямых, которые проходят через центр фигуры, получим равенство 6S = 91 + 5х. А если сложить шесть сумм чисел, лежащих на прямых, которые содержат стороны шестиугольника, то получим равенство 6S + 4х − 3S = 91 (поскольку числа в вершинах шестиугольника вошли дважды, то для того, чтобы справа получилась сумма всех чисел, пришлось правильное число раз учесть еще и центральное число, и суммы чисел на диагоналях).

Решая систему из этих двух уравнений, находим S = 21 и х = 7. Значит, в центре фигуры стоит число 7, а сумма чисел, расположенных вдоль каждого отрезка равна 21.

Рис. 2.

Все числа от 1 до 13 (которые нам и нужно расставить) разобьем, в зависимости от того, какие они дают остатки при делении на 3, на три множества. К множеству A отнесем числа, дающие при делении на 3 остаток 1 (то есть такие числа, которые можно записать в виде 3k + 1): А = {1, 4, 7, 10, 13}. Множество B — это числа, дающие остаток 2: В = {2, 5, 8, 11}; множество C — это числа, которые делятся на 3 без остатка: С = {3, 6, 9, 12}.

Учитывая, что число 21 делится на 3, можно показать, что числа из множеств А, В и С в кружочках фигуры могут располагаться только так, как показано на рис. 2.

Так как в центре стоит 7 ∈ А, числа из множества А (с точностью до симметрии и поворотов) могут располагаться только двумя различными способами (рис. 3).

Рис. 3.

Но так как сумма чисел, расположенных вдоль каждого отрезка, равна 21, то каждый из этих способов можно продолжить только двумя вариантами. В итоге получается всего четыре различных решения (рис. 4).

Рис. 4.

Рис. 5.

Человек с давних времен приписывал числам магические свойства и строил числовые схемы, обладающие интересными свойствами. Примерами служат таблица Пифагора (древнейшему найденному экземпляру около 4000 лет), треугольник Паскаля (который индийские математики исследовали еще в X веке, то есть задолго до Паскаля), и, конечно, магические квадраты.

На рисунке 5 приведен магический квадрат 3×3 с суммой 15 (это первый нетривиальный пример). Нетрудно показать, что числа от 1 до 9 расставить по-другому нельзя, то есть такой квадрат — единственный. Эта старинная числовая схема была известна еще в Древнем Китае.

Древнейшее изображение этого квадрата сохранилось на черепаховом панцире, числа на котором были изображены точками. Этому «дизайну» иногда отдают дань и сейчас — например, на марках и памятных монетах (рис. 6).

Рис. 6. Слева: блок с почтовой маркой, выпущенный в 2014 году в китайском Макао. Справа: монета номиналом 100 тенге, выпущенная в 2014 году в Казахстане

Существуют магические квадраты и больших размеров, но мы пойдем по пути другого обобщения и шагнем в трехмерное пространство. Попробуем построить магический куб 3×3×3, заполненный различными натуральными числами от 1 до 27 так, чтобы суммы чисел в любом из 27 рядов, параллельных ребрам куба, а также на четырех главных диагоналях куба и на отрезках, соединяющих середины противоположных ребер куба, были равны одному и тому же числу — магической константе S (если потребовать, чтобы и вдоль диагоналей любого параллельного граням слоя толщиной в один кубик сумма была той же, то получится то, что называют совершенным магическим кубом, см. Perfect magic cube, но наименьшая длина стороны, при которой он существует, равна 5, причем пример был построен только в 2003 году!). Говорят, что сам Альберт Эйнштейн на досуге интересовался этой задачей и построил свой магический куб 3×3×3. Попутно выясним количество таких кубов.

Чтобы вычислить магическую постоянную S, нужно сумму 1 + 2 + 3 + ... + 27 = 378 всех чисел уменьшить в 9 раз. Получим, что S = 42. Число x, расположенное в центре куба, можно найти из уравнения 13S = (1 + 2+ ... + 27) + 12x. Уравнение это составлено на основе того, что в кубе 3×3×3 есть 13 троек чисел, каждая из которых содержит центральное число х, и при этом каждое из чисел от 1 до 27, кроме самого x, входит в какую-то одну из троек. Решив уравнение, получим, что центральное число x = 14. Как же расставить остальные числа?

Иногда случается так, что на помощь в решении одной задачи приходит другая задача, на первый взгляд, напрямую с ней не связанная. Так произошло и с построением магического куба 3×3×3.

Оказывается, каждое из решений рассмотренной нами задачи про магическое колесо лежит в основе магического куба 3×3×3. Покажем это на примере первого решения. Если «колесо» слегка деформировать, то можно из него получить пространственный шестиугольник, смежные стороны которого взаимно перпендикулярны и совпадают с шестью ребрами куба (рис. 7, слева).

Рис. 7.

Далее нужно деформированное «колесо» достроить до куба 3×3×3, добавив недостающие ребра и ячейки на них (рис. 7, в центре), и удвоить уже расставленные числа. Проделав это, получим расстановку всех четных чисел магического куба. Теперь, без особого труда, остается в свободные ячейки расставить нечетные числа, учитывая, что магическая сумма равна 42. Место каждого нечетного числа определяется однозначно.

Взяв за основу другие решения «колеса», можно построить еще три магических куба (рис. 8). Таким образом, можно утверждать, что всего существует четыре магических куба 3×3×3.

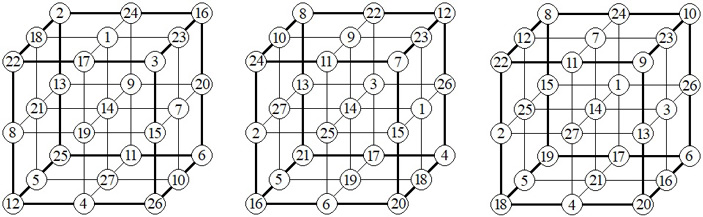
Рис. 8.