Прямое на кривом, или Прогулки по искривлённой поверхности (продолжение)

Валерия Сирота
«Квантик» №9, 2020

Продолжение. Начало в «Квантике» №8, 2020.

В прошлом номере «Квантика» мы обсудили, что значит «идти прямо» по кривой поверхности. Такие «прямые» линии называются геодезическими, и на каждом достаточно маленьком, почти плоском кусочке поверхности они должны не отличаться от обычной прямой линии. Главное — не смотреть куда-то вдаль, а идти прямо ближайшие пару шагов! А потом ещё пару... Мы также узнали, как просто и удобно изготовить две поверхности — цилиндр и конус. Теперь представим себе, что Очень Маленькое Существо идёт прямо, не сворачивая, по Очень Длинному Цилиндру — каков будет его путь?

Прогулка по цилиндру

Рис. 6

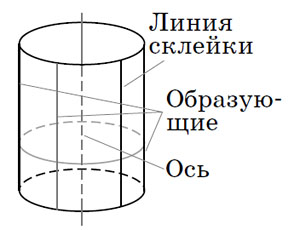
Цилиндр делается из прямоугольного листа бумаги склеиванием двух противоположных сторон (рис. 6). А сам лист, до того как его склеили, называется развёрткой цилиндра.

Выберем точку где-нибудь на цилиндре. Из неё можно идти в разные стороны, поэтому через неё проходит множество геодезических — например образующая¹ (если пойти параллельно оси цилиндра, то с образующей никуда не свернёшь). Другая геодезическая — окружность: по ней мы пройдём, если начнём двигаться перпендикулярно образующей. А если пойти куда-то ещё, между этими двумя направлениями?

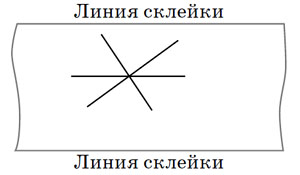
Рис. 7. Развёртка цилиндра и кусочки нескольких геодезических, проходящих через одну точку. Образующие цилиндра — горизонтальные прямые

Помните? — Важны только достаточно близкие точки, дальше двух шагов вперёд смотреть не надо! Поэтому можно спокойно развернуть обратно наш лист бумаги (если уже успели склеить, придётся разрезать по одной из образующих). Ведь маленький, почти плоский кусочек цилиндра — это то же самое, что маленький кусочек его развёртки. И чертить геодезическую на этом плоском листе гораздо удобнее, чем на цилиндре!

Итак, от выбранной нами точки где-нибудь в середине развёртки надо нарисовать маленький отрезок прямой, потом продлить его ещё чуть подальше... Да ведь просто прямая получается (рис. 7)!

Или нет?.. Когда мы добираемся до линии склейки, возникает небольшая проблема. Куда дальше идти? Как продлить путь за линию склейки?

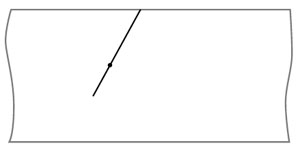
Рис. 8. Фрагмент геодезической на развёртке цилиндра

Задача 1. Дорисуйте геодезическую на развёртке цилиндра на рисунке 8. Когда начертите, не забудьте сложить цилиндр и проверить, похожа ли геодезическая в районе склейки на прямую.

Решение на следующей странице, а пока вы думаете — вот ещё такая же задачка про конус.

А теперь — конус!

Если склеить конус из прямоугольного листа, основание будет неровным и даже с торчащими углами. Но можно обрезать развёртку заранее так, чтобы никаких углов не было, а основанием нашего конуса была красивая, аккуратная окружность.

Задача 2. а) По какой линии нужно обрезать развёртку, чтобы при склеивании бумажного конуса его основание оказалось окружностью?

б) (чуть посложнее) Какой угол раствора конуса получится из такой развёртки?²

Пора идти гулять! Однако не спешите склеивать ваш конус, потому что, как и в случае с цилиндром, геодезические гораздо удобнее рисовать на развёртке.

Задача 3. Выберите какую-нибудь точку на вашей развёртке (не на линии склейки) и проведите через неё карандашами разных цветов

1. геодезическую, проходящую через вершину конуса (она называется образующей конуса);
2. геодезическую, которая на этой развёртке параллельна линии склейки;
3. геодезическую, которая на этой развёртке перпендикулярна линии склейки.

Рис. 9. Развёртка конуса и сам конус

Кусочки некоторых из этих линий уже есть на рисунке 9, нужно продолжить их. Постарайтесь нарисовать или хотя бы представить себе, как эти линии будут выглядеть на «собранном» конусе. Потом сложите из вашей развёртки конус и проверьте.

Не забудьте, что идти прямо можно в обе стороны! Геодезическая не может взять да и закончиться «в чистом поле», посреди конуса... Исключение — особенная геодезическая, которая приводит в вершину конуса. Там сама поверхность негладкая — такой уж острый кончик, что совершенно непонятно, как можно его пересечь. В природе, конечно, таких совсем острых кончиков не бывает, они всегда скруглены как-нибудь — и тогда по ним пройти можно.

Задача 4. Рисуем (лучше на новом листе) самый общий случай — геодезическую, которая из выбранной нами точки на развёртке (и конусе) выходит в произвольном направлении (например, красная линия на рисунке 9). Опять важно понять, что делать при пересечении линии склейки. Помните — в окрестности каждой своей точки геодезическая похожа на прямую! А в конце сложите конус, убедитесь, что на получившейся линии нет изломов и углов.

***

Рис. 10. Геодезическая на цилиндре

Решение задачи 1. Перейдя линию склейки, мы окажемся на нижней границе развёртки, ровно под тем местом, где достигли верхней границы. Дальше нужно продолжать двигаться в том же направлении, значит, угол между линией дальнейшего пути и образующей цилиндра (линией склейки) останется тем же, что и до перехода через линию склейки. Поэтому дальнейший путь пойдёт по отрезку прямой, параллельной отрезку на рисунке 10. Вскоре мы опять, уже второй раз, доберёмся до верхней линии склейки... Такие отрезки-продолжения нужно рисовать по обе стороны от начальной точки. В итоге на развёртке получится набор параллельных друг другу равноудалённых отрезков. А на цилиндре — винтовая линия.

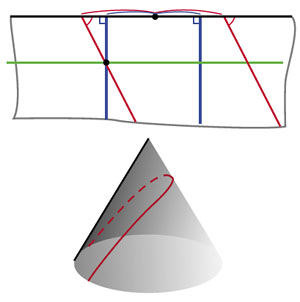
Рис. 11. Геодезические на конусе

Решение задач 3 и 4. Опять, пока мы не дошли до линии склейки, все линии на развёртке — прямые (рис. 11). При переходе линии склейки на развёртке конуса мы попадём в точку на второй линии склейки, на том же расстоянии от вершины. Чтобы продолжать идти в ту же сторону, нужно, чтобы угол, образуемый новой прямой с линией склейки, остался прежним, причём если мы шли «от вершины» (вверх и влево), то и дальше надо идти «от вершины» (теперь уже вниз и вправо).

***

Если вы справились с последними двумя задачами — или хотя бы посмотрели решение, — вы, наверно, заметили, что все геодезические, как их ни строй и куда ни направляй из выбранной точки, получаются очень похожими³. Отличаются они всего одним параметром: минимальным расстоянием до вершины.

Задача 5. На всех развёртках геодезических из задач 3–4 отметьте это минимальное расстояние, то есть для каждой геодезической найдите точку, которая ближе всех к вершине конуса.

И ещё одно замечательное свойство этого конуса: «концы» любой геодезической параллельны друг другу и на выкройке, и на конусе. Забавно, да? «Прямая» параллельна самой себе... В самом деле — например, у геодезической, параллельной образующей (пункт а в задаче 4), это явно видно: на развёртке оба её «конца» параллельны линии склейки. При складывании развёртки в конус всё это искажается, и параллельность, вообще говоря, нарушается (прямая на развёртке вообще перестаёт быть настоящей прямой, хотя и остаётся геодезической на конусе). Но вдали от вершины конуса любой небольшой участок его поверхности всё меньше отличается от кусочка плоскости, а расстояние от этих «концов» до бывшей линии склейки остаётся тем же самым. Поэтому «концы» геодезической оказываются почти настоящими прямыми, при этом почти параллельными! И чем дальше от вершины конуса, тем они «параллельнее»⁴.

Но почему же все геодезические одинаковы?

Оказывается, задачу 4 можно было бы и не решать — любую геодезическую, из любой точки и в любую сторону, можно построить так, как в задаче 3, если использовать один хитрый приём.

«Переклейка»

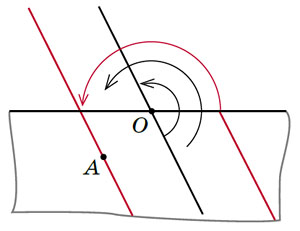
Рис. 12

Идея этого приёма в том, что развёртку конуса можно получить, разрезая его по любой образующей. Например, надо провести геодезическую через точку А в заданном направлении (рис. 12). Вместо того чтобы разбираться, как она пересечёт линию склейки, можно эту линию склейки просто перенести! Проведём через точку О (будущую вершину конуса) на нашей развёртке прямую, параллельную этому самому заданному направлению будущей геодезической. По этой линии разрежем нашу развёртку, потом повернём один из образовавшихся треугольных секторов вокруг точки О и склеим по старой линии склейки. Получилась новая развёртка, на которой искомая геодезическая — прямая, параллельная новой линии склейки. Заодно мы доказали, что все геодезические на конусе отличаются лишь одним параметром — минимальным расстоянием до вершины.

Конечно, «переклейка» помогает не всегда. Так что умение построить любую геодезическую на любой развёртке все равно пригодится. Но, даже не пользуясь ножницами и клеем, иногда полезно делать «переклейку» мысленно — представлять себе, какая картинка получилась бы при этой процедуре. Вот пример:

Задача 6. Возьмём развертку конуса с двумя точками A и B на ней. Постройте на ней все геодезические, по которым можно прийти из А в В. А как эти геодезические выглядят на конусе? Проверьте.

Решив эту задачу, вы научитесь не просто идти по «прямой» куда глаза глядят, а достигать намеченной цели, идя только прямо. Вот ещё одна такая задача.

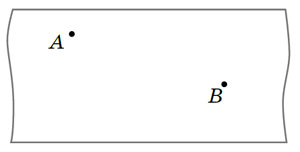
Рис. 13

Задача 7. На развёртке цилиндра заданы две точки А и В (рис. 13). Найдите все геодезические, проходящие через обе эти точки. Как выглядят эти геодезические на самом цилиндре? Как построить их на развёртке?⁵

Как строить путь из одной точки в другую на цилиндре и на конусе, мы подробно обсудим в следующем номере. Если вы уже в этом разобрались, подумайте ещё вот над чем. Конусы ведь можно делать и более широкими, и более узкими — для этого надо склеивать края не у полуплоскости, а у сектора с другим углом — например, 270° или 90°. Как выглядят геодезические на таких развёртках и на соответствующих конусах?

Художник Алексей Вайнер

Окончание следует.

¹ Заметим, что на склеенном цилиндре линия склейки уже ничем не выделяется, не отличается от других образующих. И чтобы получить развёртку, можно разрезать цилиндр по любой образующей.

² Подсказка. Для решения этой задачи полезно знать, что такое π. Решение — в конце журнала.

³ Обратите внимание, что окружности, параллельные основанию конуса, — не геодезические! Чтобы обходить конус по кругу, «не теряя высоты», придётся всё время чуть-чуть поворачивать.

⁴ Это, кстати, показывает, что геодезическая линия на конусе не является плоской кривой, то есть не лежит ни в какой плоскости. Ведь иначе она получалась бы разрезанием конуса по этой плоскости. Но при любом разрезании конуса получаются или окружности, или эллипсы, или фигуры с «расходящимися краями» — параболы и гиперболы.

⁵ Подсказка. Первую нарисовать легко, она соединяет точки А и В отрезком. Вторая геодезическая должна пересекать линию склейки цилиндра — в задаче 1 мы видели, как выглядят такие геодезические. Как добиться, чтобы она прошла через точку B? Нужно придумать способ, как по А и В найти на развёртке точку, где геодезическая пересекает линию склейки. А может, есть и ещё подходящие геодезические?..

Ответы

2. а) По полуокружности с центром в будущей вершине конуса: ведь все точки основания готового конуса находятся на одинаковом расстоянии от его вершины.

б) Длина полуокружности радиуса R на развёртке равна длине целой окружности — основания конуса (πR = 2πr); значит, R = 2r, и угол раствора равен 60°.

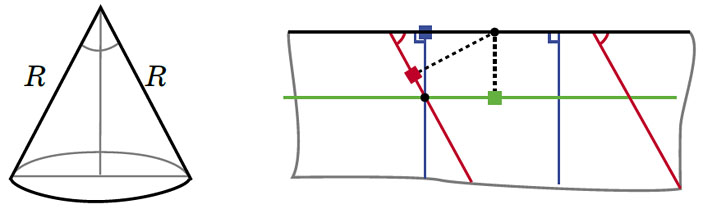
5. Ближайшая к вершине точка — та, в которой направление на вершину перпендикулярно геодезической. На развёртке тоже нужно опустить из центра конуса перпендикуляр на геодезическую.

7. Ещё подсказка: вспомните про «переклейку» конуса. Как бы тут, в цилиндре, сделать что-нибудь похожее?