Плитки и числа Хееша
Хайдар Нурлигареев
«Квантик» №10, 2019

Перед вами несколько замощений плоскости одинаковыми плитками (рис. 1). В каждом из них все плитки — копии одного и того же многоугольника. Выложить замощение можно, например, так: начать с одной плитки и постепенно обкладывать её со всех сторон другими, слой за слоем, без зазоров и наложений. Так мы доберёмся до каждого участка плоскости.

Конечно, тут не любая плитка годится — например, копиями правильного пятиугольника не выложить даже первый слой (рис. 2).

Рис. 2
А бывает ли, что несколько слоёв выкладываются, а дальше не получается? Даже если перекладывать уже выложенные слои всеми возможными способами, перебирая все варианты?
Так мы приходим к замечательному определению: числом Хееша плитки называется максимальное число слоёв, которое возможно выложить вокруг неё копиями этой плитки (при этом копии разрешается переворачивать).
У правильного треугольника, квадрата и правильного шестиугольника число Хееша равно бесконечности. А у всех остальных правильных многоугольников число Хееша равно нулю — даже первый слой выложить нельзя. Оказывается, у наугад выбранной плитки число Хееша тоже обычно либо 0, либо бесконечность.
Но существуют ли многоугольники с числом Хееша 1, 2, 3, ...? До того как Генрих Хееш сформулировал эту задачу в 1968 году, была известна лишь одна плитка с числом Хееша, отличным от 0 и бесконечности (рис. 3). Плитка эта даже не многоугольник и впервые появилась в книге Вальтера Литцмана «Забавные и странные числа и формы» в 1922 году.

Рис. 3
Сам Хееш нашёл другую плитку с числом Хееша, равным 1: это 5-угольник, составленный из квадрата, правильного треугольника и половинки такого же треугольника (рис. 4).

Рис. 4
Первый пример плитки с числом Хееша, равным 2, привела в 1991 году Энн Фонтен и даже построила бесконечно много таких плиток. Все они составлены из одинаковых квадратиков, то есть это фигурки полимино (рис. 5).

Рис. 5
В том же году Роберт Амманн добавил к правильному шестиугольнику два выступа, вырезал три таких же паза и получил фигуру с числом Хееша, равным 3 (рис. 6). Идея Амманна простая и изящная — надо искать плитку, у которой есть выступы и такие же пазы, но их разное количество.

Рис. 6

Рис. 7
Покажем, как работает эта идея, на примере плитки, найденной Кейси Манном в 2001 году. Она имеет вид четырёхклеточного прямоугольника с четырьмя выступами и пятью пазами (рис. 7). Объясним, почему число Хееша такой плитки не может быть слишком большим. Рассмотрим квадрат S, целиком покрытый копиями нашей плитки. Так как каждый паз может быть закрыт только таким же выступом, число пазов и выступов, попавших внутрь квадрата S, одно и то же. С другой стороны, число выступов внутри квадрата примерно равно его площади (в клетках) — так как у каждой клетки в плитке ровно один выступ, а число пазов примерно равно 5/4 его площади — так как в плитке на каждые 4 выступа приходится 5 пазов. Но при большом размере квадрата эти числа не могут быть равны.
Рис. 8
Вот строгое рассуждение (его можно пропустить, если «и так всё понятно»). Пусть квадрат S размера 2n × 2n полностью покрыт плитками. Для этого потребуется по крайней мере плиток. Всего у них 5n2 пазов, они все должны быть заполнены.
С другой стороны, эти пазы находятся внутри квадрата S′ размера 2(n + 4) × 2(n + 4) (рис. 8). Поэтому их заполняют выступы от не более чем 2(n + 5) · 2(n + 5) клеток (мы учли, что тут могут потребоваться выступы и от клеток, примыкающих к квадрату S′). Тем самым, выступов максимум 2(n + 5) · 2(n + 5) = 4n2 + 40n + 100. А при n > 100 заведомо выполнено неравенство n2 > 40n + 100, откуда 5n2 > 4n2 + 40n + 100, то есть пазов больше, чем выступов. Противоречие — все пазы не могут быть заполнены.
Значит, число Хееша этой плитки конечно. На самом деле, оно равно 3 (рис. 9), но доказать это получается пока только компьютерным перебором.

Рис. 9
Наиболее просты для исследования фигурки полимино, а также полиамонды и полигексы. Они тоже составлены из одинаковых «клеточек», примыкающих друг к другу сторонами, только в полиамондах клетка — это правильный треугольник, а в полигексах — правильный шестиугольник. Строя замощения из полимино, полиамондов или полигексов, мы как бы выкладываем их на свою «клетчатую» бумагу (рис. 1). На такой бумаге легко организовать компьютерный перебор. Так Кейси Манн нашёл полиамонд с числом Хееша, равным 3 (рис. 10).

Рис. 10
Также Кейси Манну удалось получить несколько новых серий полимино и полигексов с выступами и пазами, у которых число Хееша конечно, но не равно нулю. А рекордсменом является полигекс Кейси Манна, составленный из пяти шестиугольников (с выступами и пазами) — его число Хееша равно пяти (рис. 11). На сегодняшний день это плитка с самым большим известным человечеству конечным числом Хееша.
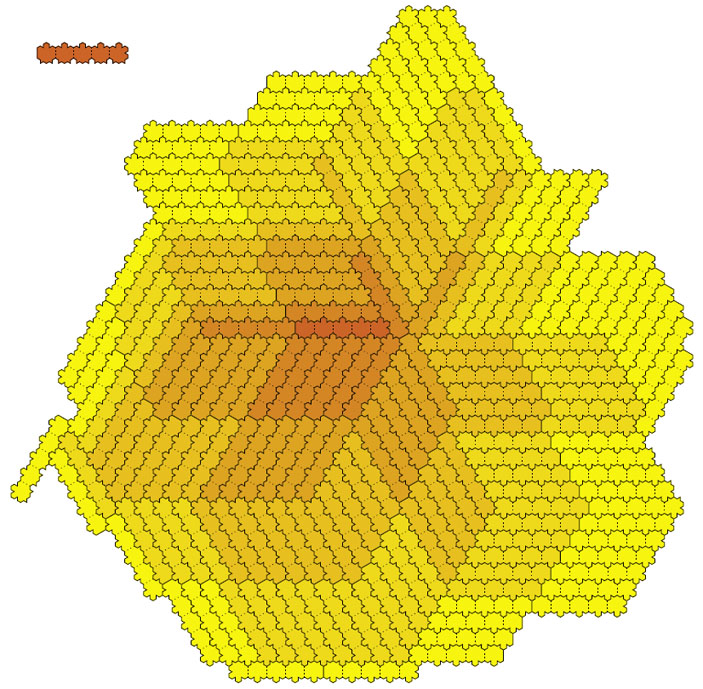
Рис. 11
Художник Алексей Вайнер
Мозаики и замощения
-
 30.07.2025Апериодическая плиткаХайдар Нурлигареев • Библиотека • «Квантик» №11, 2024
30.07.2025Апериодическая плиткаХайдар Нурлигареев • Библиотека • «Квантик» №11, 2024 -
 21.07.2021Замощения параллелоэдрамиАлексей Гарбер • Библиотека • «Квант» №1, 2019
21.07.2021Замощения параллелоэдрамиАлексей Гарбер • Библиотека • «Квант» №1, 2019
-
 03.06.2021Мозаика РобинсонаХайдар Нурлигареев • Библиотека • «Квантик» №10, 2020
03.06.2021Мозаика РобинсонаХайдар Нурлигареев • Библиотека • «Квантик» №10, 2020
-
 30.05.2021Оклейка тетраэдра шестиугольникамиНиколай Авилов • Библиотека • «Квант» №10, 2018
30.05.2021Оклейка тетраэдра шестиугольникамиНиколай Авилов • Библиотека • «Квант» №10, 2018
-
 06.12.2020Как разрезать верблюда?Григорий Мерзон • Библиотека • «Квантик» №5, 2020
06.12.2020Как разрезать верблюда?Григорий Мерзон • Библиотека • «Квантик» №5, 2020
-
 03.06.2020Плитки и числа ХеешаХайдар Нурлигареев • Библиотека • «Квантик» №10, 2019
03.06.2020Плитки и числа ХеешаХайдар Нурлигареев • Библиотека • «Квантик» №10, 2019
-
 09.08.2019Ковер СерпинскогоХайдар Нурлигареев • Картинки дня
09.08.2019Ковер СерпинскогоХайдар Нурлигареев • Картинки дня
-
 18.10.2018Самоподобные замощенияХайдар Нурлигареев • Картинки дня
18.10.2018Самоподобные замощенияХайдар Нурлигареев • Картинки дня
-
 14.09.2018Мозаика РобинсонаХайдар Нурлигареев • Картинки дня
14.09.2018Мозаика РобинсонаХайдар Нурлигареев • Картинки дня
-
 16.04.2018«Жесткие» замощенияХайдар Нурлигареев • Задачи
16.04.2018«Жесткие» замощенияХайдар Нурлигареев • Задачи























Рис. 1