Брызгалки и многогранники

Дмитрий Панов, Александра Пушкарь, Дмитрий Чебасов
«Квантик» №3, 2018

Этот текст написан по мотивам статьи «Вдогонку лету» из «Квантика» № 10 за 2017 год, где было рассказано, как из трубочек и маленьких резиновых колечек для плетения сделать простую брызгалку.

Здесь мы используем те же самые материалы и технологии для проведения геометрических построений. Подходящие для наших экспериментов трубочки продаются в магазине «Весёлая затея» и называются там палочками для воздушных шаров. Они достаточно длинные — 37,5 см — и при этом одновременно жёсткие и упругие. Маленькие резиновые колечки для плетения продаются практически в любом магазине.

Рис. 1. Равносторонний треугольник

Сначала мы взяли три трубочки и попарно скрепили их концы резиновыми колечками. Получился равносторонний треугольник (рис. 1). А почему бы не собрать из тех же трубочек квадрат? И вот тут нас ожидал сюрприз. Мы соединили как надо четыре одинаковые трубочки, но это был не совсем квадрат или даже совсем не квадрат. Если положить эту конструкцию на стол, она мгновенно превращается в ромб, а если приподнять за вершину, то и вовсе перестаёт быть плоской фигурой (рис. 2). Мы назвали этот четырёхугольник непослушным квадратом.

Рис. 2. Непослушный квадрат

Математики называют фигуры, которые легко меняют свою форму, изгибаемыми. Так вот, треугольник, состоящий из трёх отрезков, жёсткий — неизгибаемый, а квадрат и любой четырёхугольник, и пятиугольник, и шестиугольник и т. д. — изгибаемы. Это хорошо известный факт, и мы смогли убедиться в нём с помощью трубочек и резиночек.

А почему бы теперь не собрать что-нибудь пространственное? И мы легко собрали из трубочек самый простой многогранник — треугольную пирамиду (рис. 3). Правда, в математике многогранником называют другой объект — каркас вместе с гранями-многоугольниками (рис. 4).

Рис. 3 (слева). Каркас пирамиды. Рис. 4. «Настоящая» пирамида

При этом общие отрезки соседних граней называются рёбрами — они соответствуют нашим трубочкам. А точки, где сходятся несколько рёбер, называются вершинами — можно сказать, что это наши резиночки.

Вот ещё два замечательных многогранника: из 12 трубочек собирается октаэдр, у него 8 граней, а из 30 трубочек — икосаэдр, у него 20 граней (рис. 5).

У всех трёх собранных многогранников все грани треугольные, и эти многогранники неизгибаемые.

Рис. 5. Трубчатые октаэдр и икосаэдр

Теперь попробуем собрать из трубочек куб. Посмотрите на рисунок 6: этот куб совсем не держит форму — он изгибаем, и изгибаем совершенно чудовищным образом. Мы назвали его разболтанным кубом.

А если без шуток, то тут возникает серьёзный математический вопрос: какие многогранники, собранные из трубочек, изгибаемы, а какие нет? Конечно, трубочки и резиночки могут что-то подсказать, но различных многогранников слишком много, чтобы без строгого доказательства доверять этим подсказкам. У нас появились кое-какие предположения, но мы не были уверены в них.

Рис. 6. Разболтанный куб

К счастью, сейчас в интернете есть места, где на трудный математический вопрос можно получить квалифицированный ответ. Самое известное из них — сайт профессиональных математиков MathOverflow. Там обсуждаются многие вопросы, связанные с современными математическими исследованиями, а также нерешённые математические проблемы, но совсем не приветствуются вопросы непрофессиональные или вопросы типа домашних заданий. С некоторой опаской мы обратились туда и спросили: если взять выпуклый многогранник, то есть многогранник без впадин (рис. 7), и убрать из него все грани, а оставить только рёбра (тогда как раз получится что-то вроде нашего многогранника из трубочек), в каком случае он будет изгибаемым, в каком — нет?

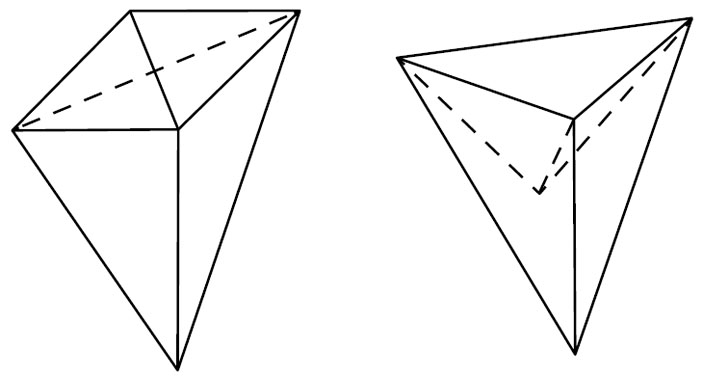
Рис. 7. Выпуклый многогранник — без впадин, а у невыпуклого впадины имеются

Нас порадовало, что ответ был получен, и довольно быстро. Как мы и предполагали, если в многограннике есть хоть одна не треугольная грань, он будет изгибаемым, а если все грани треугольные, он — жёсткий.

Обсуждение нашего вопроса на MathOverflow¹ было очень интересным. В самом начале было сказано, что из теоремы Коши следует неизгибаемость трубчатого выпуклого многогранника. После этого Джозеф О’Рурк² привёл пример многогранника с квадратной гранью, который, как он считал, неизгибаем (рис. 8). Мы собрали этот многогранник из трубочек (рис. 9), и оказалось, что О’Рурк ошибся — многогранник прекрасно изгибался.

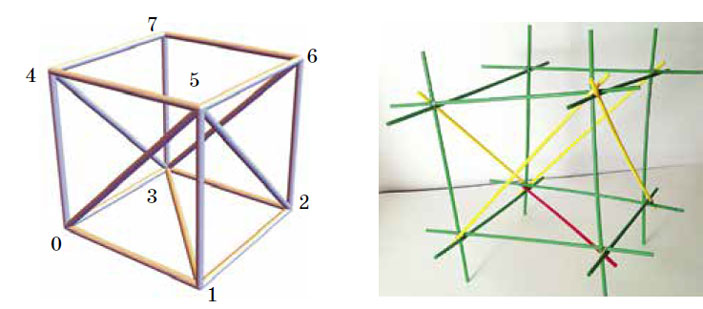
Рис. 8 (слева). Многогранник О’Рурка. Рис. 9. Многогранник О’Рурка изгибаем

А затем Антон Петрунин³ привёл простое доказательство изгибаемости трубчатого многогранника, у которого есть хотя бы одна не треугольная грань. В своем доказательстве он использовал теорему А. Д. Александрова. Вот так был получен ответ на наш вопрос.

Упомянутые здесь теоремы Коши и Александрова — самые знаменитые в теории многогранников. Их формулировки достаточно просты, а доказательства доступны старшим школьникам. Советуем почитать книжку Н. Долбилина⁴ «Жемчужины теории многогранников» (М.: МЦНМО, 2012), посвященную доказательствам этих теорем и рассчитанную на школьников.

Несколько слов в заключение. Важным классическим вопросом является вопрос о жёсткости и изгибаемости настоящих многогранников — многогранников с гранями. Здесь есть красивая теория с большой историей и с неожиданными открытиями, частично доступная школьникам. Советуем прежде всего посмотреть в интернете популярную лекцию «Изгибаемые многогранники и кузнечные мехи», год назад прочитанную Александром Гайфуллиным⁵ на XXVIII Математическом празднике в Москве для 6- и 7-классников.

Фото: Дмитрий Чебасов
Художник Алексей Вайнер

¹ Если вы знаете английский, можете посмотреть это обсуждение, набрав в Google «Rigidity of convex polyhedron in R3 with faces removed».

² На MathOverflow каждому участнику добавляют очки за популярные вопросы и популярные ответы. Среди 64 000 участников О’Рурк по популярности идёт на третьем месте, у него 80 000 баллов.

³ А. Петрунин — один из авторов журнала «Квант», профессор университета Penn State.

⁴ Н. П. Долбилин — ведущий научный сотрудник Математического института им. В. А. Стеклова, автор статей в «Кванте» и «Квантике».

⁵ А. Гайфуллин — сотрудник механико-математического факультета МГУ, член-корреспондент Российской академии наук.