Экономичное занятие

Игорь Акулич
«Квантик» №5, 2019

— Сегодняшнее занятие нашего математического кружка назовём экономичным.

— Деньги будем считать?

— Нет, трудозатраты в простейших геометрических построениях циркулем и линейкой.

Напомню, что взяв линейку, мы можем выбрать две любые точки и провести через них прямую. Взяв же циркуль, мы можем измерить им расстояние между двумя любыми точками, а потом поместить остриё циркуля в любую точку и провести окружность, радиус которой равен этому расстоянию. Иногда, чтобы не загромождать чертёж, проводят не окружность целиком, а только её часть, то есть дугу.

А теперь задача: на плоскости даны прямая l и точка М вне её. Кто построит циркулем и линейкой перпендикуляр p к прямой l, проходящий через точку М?

— Я!

— Я!

— ...

— Вижу, что все готовы. Давайте вы, пожалуйста!

Рис. 1

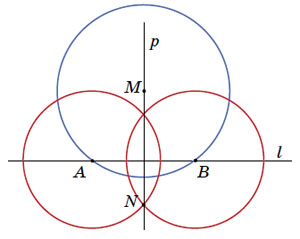
— Сначала выбираем на прямой l произвольную точку А и проводим окружность радиусом МА с центром в точке М, пересекающую прямую l ещё и в точке В (синяя окружность на рисунке 1). Затем проводим ещё две окружности одинакового радиуса с центрами в точках А и В (красные окружности на рисунке 1). Через точку N пересечения красных окружностей и точку М проводим прямую — это и будет перпендикуляр p.

— Что ж, построение безупречно. Но есть несколько вопросов. Во-первых, можете ли вы доказать, что прямая p — действительно перпендикуляр к прямой l?

Рис. 2

— Конечно. Соединим точки так, чтобы получился четырёхугольник AMBN (рис. 2). Стороны треугольников МАN и МBN соответственно равны (по построению). Значит, и сами треугольники равны и «приложены» с разных сторон к общей стороне MN. Поэтому они симметричны друг другу относительно MN. А из симметрии точек А и В следует, что они лежат на одном перпендикуляре к оси симметрии. Так что АВ ⊥ МN.

— Верно. Добавлю, что четырёхугольник, у которого две соседние стороны равны между собой и две другие тоже равны, называется дельтоид. Как раз таков четырёхугольник AMBN (в нём МА = МB и АN = BN). И здесь вы между делом доказали, что диагонали дельтоида взаимно перпендикулярны.

Теперь второй вопрос: а если синяя окружность пересекла прямую l только в одной точке А (иначе говоря, точки В и А совпали)? Тогда мы не сможем провести две красные окружности. Как здесь быть?

— Я понял! Если синяя окружность имеет с прямой l лишь одну общую точку, то прямая касается окружности. Так как касательная перпендикулярна радиусу, проведённому в точку касания, отрезок МА перпендикулярен прямой l. То есть надо сразу провести прямую через точки М и А — это и будет искомый перпендикуляр.

— Прекрасно. Отмечу только, что так удачно выбрать наугад из бесконечного количества точек прямой единственную лежащую на перпендикуляре — практически нереально (да и теоретически тоже).

И последний вопрос: как построить перпендикуляр, если точка М лежит на прямой l?

— Точно так же! Проводим синюю окружность, получаем точки А и В — и так далее...

— Что ж, вижу, материал из учебника усвоен вами накрепко. А теперь нечто новое: займёмся оценкой трудоёмкости выполненных построений. Давайте считать, что проведение любой линии (прямой или окружности) — это один «ход». Сколько ходов потребовалось для построения перпендикуляра?

— Четыре: три окружности (синяя и две красных) и потом прямая (то есть сам перпендикуляр).

Рис. 3

— А можно быстрее! Снова берём прямую l и точку М вне её. Выбираем на прямой l произвольную точку А и проводим окружность радиусом АМ с центром в А (синяя окружность на рисунке 3). Затем выбираем на той же прямой произвольную точку В и проводим окружность радиусом BМ с центром в В (красная окружность на рисунке 3). Эти две окружности пересекаются в двух точках, одна из которых — заданная точка М, а вторую обозначим буквой N. Наконец, проводим отрезок MN, который и будет искомым перпендикуляром. Итого — три хода вместо четырёх!

— А это правда перпендикуляр?

— Конечно. Если мысленно провести отрезки и образовать четырёхугольник AMBN, то в нём AM = AN (как радиусы одной окружности) и BM = BN (по той же причине). Значит, AMBN — дельтоид, только «лежащий на боку», и его диагонали перпендикулярны.

— Ничего себе! Но если М лежит на прямой l, этот способ неприменим — ведь тогда окружности касаются друг друга, и второй точки их пересечения нет!

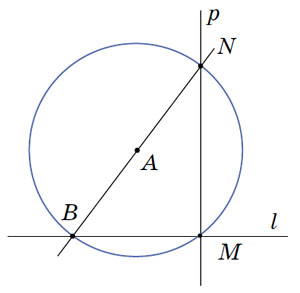
Рис. 4

— Вы правы. Но и тут есть иной способ построения, столь же экономный. Итак, пусть точка М лежит на прямой l. Сначала выбираем произвольную точку А вне прямой l и проводим окружность радиусом АМ с центром в А. Она пересечёт прямую l ещё в точке В. Через точки А и В проводим прямую, пересекающую окружность в точке N. И проводим прямую MN, которая и есть искомый перпендикуляр p (рис. 4).

— ???

— Что, совсем несуразно выглядит? А между тем доказательство тоже очень простое. Из наших построений следует, что ВN — диаметр проведённой окружности, а ∠ BMN — вписанный угол, опирающийся на этот диаметр. Но такой угол всегда прямой!

— Ух ты! Но... вдруг нам не повезёт, и мы случайно выберем такую точку А, что окружность не пересечёт прямую l во второй точке В, а будет касаться её в точке М? Иначе говоря, точки В и М совпадут?

— Наоборот, в случае такого невероятного везения можно сразу провести перпендикуляр AM — ведь если окружность касается прямой, то радиус, проведённый в точку касания, перпендикулярен касательной.

И последнее на сегодня: как через точку M, лежащую вне прямой l, провести прямую, параллельную l?

— Как два перпендикуляра! То есть сначала провести какой-нибудь перпендикуляр к прямой l, а потом — перпендикуляр к этому перпендикуляру, проходящий через ту же точку М.

— И сколько ходов для этого понадобится?

— Ну... если проводить перпендикуляры так, как говорится в учебнике, то это будет 4 + 4 = 8 ходов, а если вашими «экономными» способами, то 3 + 3 = 6.

— А можно обойтись лишь тремя ходами.

— Как?

Рис. 5

— Показываю. Выбираем на прямой l произвольную точку А и проводим окружность радиусом АМ с центром в А (синяя окружность на рисунке 5). Она пересечёт прямую l в точках В и С. Далее, строим окружность (красную) радиусом, равным ВМ, с центром в С. Она пересекается с синей окружностью в точке N (вообще-то таких точек две; надо выбрать ту, что лежит по ту же сторону от l, что и М. Наконец, проводим прямую через точки M и N — она параллельна l.

— Почему?

— Доказательство несложно и основано на симметрии. Если мысленно провести перпендикуляр к прямой l через центр синей окружности А, то полуокружности справа и слева будут симметричны между собой относительно него. И равные дуги BM и CN тоже симметричны. Значит, и точки M и N симметричны, откуда отрезок MN перпендикулярен к перпендикуляру к прямой l, то есть параллелен l. Всё!

— А почему дуги BM и CN равны?

— Так они же стягиваются равными хордами — отрезки BM и CN по построению равны.

— Здорово! А если N и М совпадут? Тогда мы не сможем провести через M и N единственную прямую.

Рис. 6

— Верно. Это может произойти, если точка А окажется точнёхонько на перпендикуляре к прямой l, проходящем через точку М. Такое событие тоже практически невероятное, но здесь это не удача, а, наоборот, неприятность. Поэтому пренебрегать ею нельзя. И в качестве альтернативы могу предложить способ чуть длиннее, из четырёх шагов. Начало такое же: выбираем на прямой l произвольную точку А и проводим окружность радиусом АМ с центром в А (синяя окружность на рисунке 6). Она пересечёт прямую l в точке В (здесь используем только одну из двух точек пересечения — любую). Далее, строим ещё две окружности такого же радиуса с центрами в точках М и В (красная и зелёная соответственно). Они пересекаются в точке N. Наконец, проводим прямую через точки M и N — она параллельна l. Доказательство несложно: если рассмотреть четырёхугольник ABNM, то по нашим построениям все его стороны равны, потому что они — радиусы одинаковых окружностей. Значит, ABNM — ромб, а у ромба противоположные стороны параллельны. Вот и всё! Ну как, понравились сегодняшние построения?

— Красиво!

— Быстро!

— Я рад, что они вам по вкусу. Пользуйтесь на здоровье. Но имейте в виду — эти экономичные построения не очень-то широко известны, и вы должны быть готовы подтвердить их справедливость безупречным доказательством. Особенно на экзамене. Поэтому не забывайте и «классические» способы. Они тоже хороши, а главное — понятны и практически очевидны.

Художник Алексей Вайнер