В начале было слово
Александр Блинков
«Квантик» №6, 2019

Юные читатели! Я уверен — ваши учителя говорили вам, что в математических высказываниях очень важна точность формулировок. Но одно дело слышать это, а совсем другое — убедиться на практике.
Рассмотрим несколько утверждений из школьного курса геометрии, которые звучат весьма правдоподобно, но верными, однако, не являются1. При этом к каждому из них достаточно добавить одно слово (возможно, в нескольких местах) — и оно станет верным!
Пример 1. Углы с соответственно перпендикулярными сторонами равны.
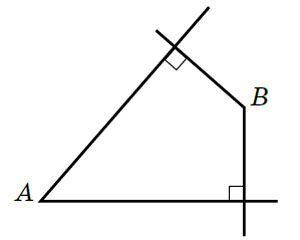
Почему это неверно? Потому, что один из углов может быть острым, а другой — тупым (углы А и В соответственно на рисунке 1).
Понятно, что вставив одно слово, мы получим верное утверждение, причём возможны два варианта: острые (тупые) углы с соответственно перпендикулярными сторонами равны.
Аналогичная ситуация возникнет и в формулировке о равенстве углов с соответственно параллельными сторонами.
Пример 2. Общие внешние касательные к двум окружностям пересекаются на прямой, проходящей через их центры.
Действительно, если такие касательные пересекаются, то точка пересечения лежит на линии центров. Но если две указанные окружности имеют равные радиусы, то их внешние касательные параллельны (рис. 2).

Рис. 2
Докажем это. Пусть А и В — точки касания равных окружностей с центрами О и О1 с одной из указанных прямых. Тогда радиусы окружностей ОА и О1В перпендикулярны прямой АВ, поэтому ОА || О1В. Кроме того, ОА = О1В, следовательно, ОАВО1 — параллелограмм, тогда АВ || ОО1 (доказано даже, что ОАВО1 — прямоугольник, но для наших целей это несущественно). Аналогично доказывается, что вторая касательная параллельна ОО1. Следовательно, касательные параллельны друг другу.
Верное утверждение такое: общие внешние касательные к двум неравным окружностям пересекаются на прямой, проходящей через их центры.
Пример 3. Прямая, разбивающая четырёхугольник на два треугольника, содержит диагональ этого четырёхугольника.
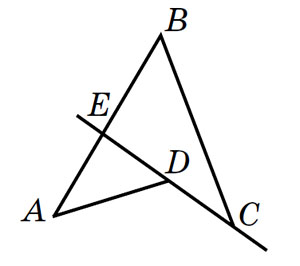
Рис. 3
В отличие от двух предыдущих примеров, понять, почему и это утверждение неверно, гораздо сложнее. Дело в том, что четырёхугольник может быть невыпуклым, и тогда его может делить на два треугольника прямая, содержащая сторону! Например, прямая CD, содержащая сторону четырёхугольника ABCD, разбивает его на два треугольника: ADE и BEC (рис. 3).
Верное утверждение: прямая, разбивающая выпуклый четырёхугольник на два треугольника, содержит диагональ этого четырёхугольника.
В некоторых случаях, для того чтобы утверждение стало верным, приходится добавить не одно слово, а целое словосочетание.
Пример 4. Если точка равноудалена от прямых, содержащих стороны треугольника, то она является центром вписанной в него окружности.

Рис. 4
Центр вписанной окружности действительно равноудалён от сторон треугольника. Но единственная ли это точка, обладающая таким свойством? Чтобы понять это, вспомним: центр вписанной окружности обладает этим свойством потому, что является точкой пересечения биссектрис всех углов треугольника. Но прямые, содержащие стороны треугольника, образуют ещё и внешние углы этого же треугольника. Тогда, например, точка Q пересечения биссектрис двух его внешних углов В и С равноудалена от их сторон, то есть равноудалена от прямых АВ, АС и ВС (рис. 4).
Подумайте: 1) Лежит ли точка Q на биссектрисе угла ВАС? 2) Сколько существует точек, равноудалённых от прямых, содержащих стороны любого треугольника?
А мы уже можем сформулировать верное утверждение, добавив словосочетание: если точка, лежащая внутри треугольника, равноудалена от прямых, содержащих стороны треугольника, то она является центром вписанной в него окружности.
Пример 5. Прямая, делящая площадь треугольника пополам, содержит его медиану.

Рис. 5
Это было бы верным, если бы указанная прямая делила треугольник на два треугольника. Но возможна иная ситуация: прямая разбивает треугольник на треугольник и четырёхугольник. Пусть дан треугольник АВС, в котором АС = 2, отрезок DE с концами на сторонах АВ и ВС параллелен АС и DE = √2 (рис. 5). Тогда треугольник АВС подобен треугольнику DBE с коэффициентом √2, откуда площадь АВС в два раза больше площади DBE. Тем самым прямая DE делит площадь треугольника АВС пополам, но не содержит медиану этого треугольника.
Для получения верного утверждения здесь также придётся добавить словосочетание: прямая, проходящая через вершину и делящая площадь треугольника пополам, содержит его медиану.
Необходимость точных формулировок (и не только в математике!) понимали ещё древние греки. Они ввели термин «логос», который в древнегреческой философии означал одновременно «слово» (высказывание, речь) и «понятие» (суждение, смысл).
В заключение — упражнения для самостоятельного решения.
Упражнения
Объясните, почему сформулированные ниже утверждения не являются верными. Измените эти утверждения, вставив слово (в заданиях 1–10) или словосочетание (в заданиях 11–17) так, чтобы утверждения стали верными.
- В треугольниках напротив равных сторон лежат равные углы.
- Если катет и прилежащий к нему угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему углу другого прямоугольного треугольника, то такие треугольники равны.
- Если две стороны и высота, проведённая к третьей стороне одного треугольника, соответственно равны двум сторонам и высоте, проведённой к третьей стороне другого треугольника, то такие треугольники равны.
- Точки плоскости, удалённые на данное ненулевое расстояние от заданной точки О, образуют окружность с центром О.
- Равные хорды окружности стягивают равные дуги.
- Две общие касательные к двум неравным окружностям пересекаются на прямой, содержащей их центры.
- Наименьший диаметр окружности, внутри которой можно поместить данный треугольник, — это диаметр окружности, описанной около треугольника.
- Средней линией трапеции называется отрезок, соединяющий середины её сторон.
- Если все стороны и диагональ одного четырёхугольника соответственно равны сторонам и диагонали другого четырёхугольника, то равны и другие их диагонали.
- Середины трёх высот треугольника не лежат на одной прямой.
- В равнобедренном треугольнике медиана является биссектрисой и высотой.
- Если точка равноудалена от сторон угла, то она лежит на биссектрисе этого угла.
- Площадь треугольника равна половине произведения стороны и высоты.
- Равным наклонным к прямой соответствуют равные проекции.
- Касательная к окружности перпендикулярна её радиусу.
- Диаметр окружности, проходящий через середину хорды, перпендикулярен ей.
- Параллелограмм не имеет оси симметрии.
Подсказки
- В любых треугольниках?
- Какие именно углы равны?
- Пусть один треугольник — остроугольный, а другой — тупоугольный.
- О каком количестве точек идёт речь?
- Хорда окружности стягивает две дуги.
- Сколько общих касательных может быть у двух окружностей?
- Рассмотрите по отдельности каждый вид треугольника (по углам).
- Соедините, например, середины основания и боковой стороны.
- Четырёхугольники бывают невыпуклыми.
- Рассмотрите по отдельности каждый вид треугольника (по углам).
- Любая медиана?
- Рассмотрите точку на луче, дополнительном к биссектрисе.
- Можно ли выбрать любую высоту?
- Сколько равных наклонных можно провести к прямой?
- Сколько радиусов можно провести в окружности?
- Будет ли хордой окружности её диаметр?
- А квадрат является параллелограммом?
Ответы
- В равных треугольниках напротив равных сторон лежат равные углы.
- Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему углу другого прямоугольного треугольника, то такие треугольники равны.
- Если две стороны и высота, проведённая к третьей стороне одного остроугольного треугольника, соответственно равны двум сторонам и высоте, проведённой к третьей стороне другого остроугольного треугольника, то такие треугольники равны.
- Все точки плоскости, удалённые на данное ненулевое расстояние от заданной точки О, образуют окружность с центром О.
- Равные хорды окружности стягивают равные меньшие (большие) дуги.
- Две общие внешние (внутренние) касательные к двум неравным окружностям пересекаются на прямой, содержащей их центры.
- Наименьший диаметр окружности, внутри которой можно поместить данный остроугольный (прямоугольный) треугольник, — это диаметр окружности, описанной около треугольника.
- Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон.
- Если все стороны и диагональ одного выпуклого четырёхугольника соответственно равны сторонам и диагонали другого выпуклого четырёхугольника, то равны и другие их диагонали.
- Середины трёх высот непрямоугольного треугольника не лежат на одной прямой.
- В равнобедренном треугольнике медиана, проведённая к основанию, является биссектрисой и высотой.
- Если точка, лежащая внутри угла, равноудалена от сторон угла, то она лежит на биссектрисе этого угла.
- Площадь треугольника равна половине произведения стороны и высоты, проведённой к ней.
- Равным наклонным к прямой, проведённым из одной точки, соответствуют равные проекции.
- Касательная к окружности перпендикулярна её радиусу, проведённому в точку касания.
- Диаметр окружности, проходящий через середину хорды, не являющейся диаметром, перпендикулярен ей.
- Параллелограмм, отличный от прямоугольника и ромба, не имеет оси симметрии.
Художник Алексей Вайнер
1 Напомним, что верными считаются утверждения, которые верны всегда. Скажем, утверждение «Четырёхугольник, все углы которого равны, является прямоугольником» верное, так как любой четырёхугольник, все углы которого равны, действительно будет прямоугольником, поскольку все его углы будут тогда прямыми. А утверждение «Четырёхугольник, все стороны которого равны, является квадратом» неверное, поскольку оно нарушается, например, для ромба с углами 60° и 120°.





















Рис. 1