Неубиваемые магнитные монополи
Тема магнитных монополей не отпускает. Совсем недавно мы рассказывали о коллективных магнитных монополях в спиновом льду и о синтетических магнитных монополях в бозе-конденсате, а также предлагали задачку, посвященную способностям магнитного монополя. В новой задаче на эту тему мы предлагаем познакомиться с необычной «живучестью» монополей в кристаллической решетке.

Магнитный монополь — это гипотетическая частица, несущая отдельный магнитный заряд. Это словно отделившийся полюс магнита, перемещающийся независимо от своего антипода и создающий вокруг себя радиально расходящееся магнитное поле. Несмотря на то, что таких частиц в природе пока не найдено, физики смогли разглядеть в некоторых веществах объекты, которые ведут себя похоже на магнитные монополи. Например, в материале, называемом спиновым льдом, могут существовать коллективные электронные образования с особыми магнитными свойствами. Они могут перемещаться по кристаллу, взаимодействуют с магнитным полем, притягиваются друг к другу — в общем, ведут себя так, как вели бы себя магнитные монополи (см. подробности в новости Разработана новая методика получения магнитных монополей в спиновом льду).
Так же, как и электрические заряды, монополи бывают разных знаков — положительные и отрицательные (условно говоря, северный и южный полюса магнита). Противоположные по знаку монополи притягиваются, одноименные — отталкиваются. Если у нас есть пара противоположных монополей в кристалле, то они из-за притяжения начнут сближаться, а когда очутятся рядом, они — казалось бы — должны неизбежно проаннигилировать. Это было бы совершенно естественное явление, которое напоминает взаимное устранение противоположных электрических зарядов — например, аннигиляцию электрона и позитрона или «сокращение» электронов и дырок в полупроводниках.
Но именно здесь аналогия между магнитными монополями и электрическими зарядами дает сбой. Оказывается, магнитные монополи противоположных знаков не всегда легко устранить! Они могут находиться совсем рядом, в шаговой доступности друг от друга, но при этом в силу некоторых причин могут не хотеть аннигилировать. В предлагаемой задаче мы познакомимся с этим явлением на примере простейшей модели.
Возьмем для примера квадратную кристаллическую решетку, в узлах которой находятся атомы, а звеньями служат валентные электроны. Каждому электрону мы присваиваем стрелочку (это его спин), которая смотрит от одного атома к другому. Будем считать, что основное магнитное состояние решетки — это когда в каждом узле две стрелочки входят, а две выходят (правило «2-2»). Будем считать, что совершенно неважно, с какой именно стороны стрелки входят, а с какой выходят — в нашей модели будет важно только их число. Пример такой ситуации показан на рис. 2.

Рис. 2. Квадратная решетка со звеньями-стрелочками, моделирующая спиновый лед. Наиболее энергетически выгодное состояние решетки — когда в каждом узле две стрелочки смотрят внутрь, а две — наружу
Теперь возьмем и перевернем одну стрелочку (рис. 3, слева). Тогда в двух соседних узлах баланс стрелочек нарушен: в одном узле (он показан красным цветом) входят три, а выходит одна (узел «3-1»), а в другом — наоборот (узел «1-3»). Эти два узла мы будем считать магнитными монополями противоположного знака.

Рис. 3. Решетки с парой монополей, получающиеся из состояния на рис. 2 переворотом одной (слева) или нескольких соседних (справа) стрелочек
Монополи не обязаны располагаться рядом. Можно, например, перевернуть еще пару соседних стрелочек, и тогда узлы вида «3-1» и «1-3» разойдутся, но никакие новые монополи при этом не появятся. Например, на рис. 3, справа, во всех узлах, кроме двух цветных, выполняется правило «2-2». Получить такую ситуацию из основного состояния кристалла можно последовательным переворотом трех стрелочек вдоль пути, подсвеченного желтым цветом. Переворачивая стрелочки дальше, можно удлинять подсвеченную линию и тем самым разнести монополи еще дальше друг от друга.
Раз пару монополей можно создать, то, значит, ее можно и устранить. Например, если на рис. 3, слева, развернуть черную стрелочку — монополи исчезнут. Далеко расположенные монополи тоже можно устранить — для этого надо просто переворачивать одну за другой стрелочки на подсвеченном пути. Тогда монополи будут постепенно сближаться, а затем и исчезнут. Но всегда ли это возможно? Оказывается, нет.
Задача
Найдите пример такой конфигурации стрелочек, при которой в решетке имеются два расположенных рядом монополя противоположного знака, которые невозможно устранить переворотом одной соединяющей их стрелочки. Выясните, что все-таки нужно сделать, чтобы эти «неубиваемые» монополи проаннигилировали.
Подсказка
Попробуйте для начала переворачивать стрелочки, стартуя с рис. 2. Вы быстро убедитесь, что любая пара рядом расположенных монополей легко устраняется. Но рис. 2 — это лишь один из возможных примеров основного состояния, а вовсе не единственная конфигурация такого типа. Можно нарисовать и другие стрелочные конфигурации, для которых правило «2-2» выполняется в каждом узле. Попробуйте построить другие решетки такого сорта и подберите в них нужный пример.
Можно, конечно, не действовать методом проб и ошибок, а сразу понять, в чем заключается особенность таких дефектов и содержащих их решеток. Догадавшись, можно тут же нарисовать подходящую решетку и найти в ней нужную пару.
Решение

Рис. 4. Пример решетки с двумя близкими монополями, соединенными длинной цепочкой неправильных спинов (выделена желтым). Устранить эту пару монополей можно последовательным переворотом пронумерованных стрелочек. В середине этого процесса монополи окажутся разнесенными довольно далеко
Один возможный (но вовсе не простейший) пример такой «неубиваемой» пары показан на рис. 4. Два соседних цветных узла — это монополи противоположного знака. Однако если попытаться перевернуть соединяющую их стрелочку, то монополи не исчезнут, а лишь усилятся, превратятся в дефекты вида «4-0» и «0-4». Убить эти монополи переворотом одной стрелочки невозможно.
Такая ситуация возможна потому, что в нашей двумерной модели есть свобода выбора. Если нарисовать дефект «3-1», то для размещения противоположного дефекта «1-3» есть две неэквивалентные ситуации. Если бы совсем упростили задачу — рассмотрели бы не плоскую решетку, а одномерную цепочку атомов с одной входящей и одной выходящей стрелочкой, — такой свободы не было бы.
Чтобы монополи на рис. 4 проаннигилировали, надо последовательно развернуть как минимум 7 пронумерованных на рисунке стрелочек. Именно вдоль этой ломаной линии (а вовсе не по кратчайшему пути!) и расположены «неправильные» стрелочки. Но последовательный переворот стрелок — это как бы перенос монополя вдоль пути, подсвеченного на рисунке. Отсюда следует вывод: для аннигиляции эту пару близких монополей надо сначала разделить, а потом соединить снова — но уже с другой стороны.
На рис. 2 и 3 такой трюк не прошел бы. Там основное состояние специально выбрано так, что, удаляя монополи друг от друга, мы удлиняем цепочку неправильных стрелочек, а сближая монополи — укорачиваем цепочку. Так получается потому, что все горизонтальные и все вертикальные ряды стрелочек смотрят в одну сторону. Если же выбрать основное состояние, в котором это не так (например, некоторые горизонтальные ряды смотрят направо, а некоторые — налево), то тогда цепочку неправильных спинов можно развернуть, как на рис. 4. Укоротить такую цепочку можно только за счет удаления монополей друг от друга.
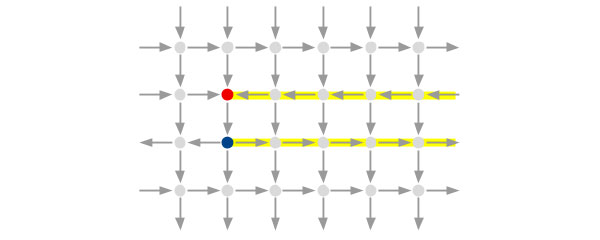
Рис. 5. Пример решетки с двумя неустранимыми монополями. Соединяющая их цепочка неправильных спинов бесконечно длинная
Не составляет труда также нарисовать такую решетку и пару монополей, для которой цепочка неправильных спинов бесконечно длинная (рис. 5). Эта цепочка словно уходит на бесконечность, там как-то перепрыгивает на один ряд, и возвращается с бесконечности ко второму монополю. Такую пару монополей убить последовательным переворотом стрелочек без создания новых монополей невозможно. С физической точки зрения тот факт, что все вертикальные стрелки смотрят в одну сторону, означает, что весь образец полностью намагничен по вертикали. Поэтому воссоединить противоположные монополи на этом рисунке не удается — у нас не осталось для этого ни малейшей возможности.
Послесловие
Полученный нами вывод объясняет, почему в реальной ситуации такая пара монополей, даже соединенная цепочкой конечной длины, может быть стабильна. Монополи противоположных знаков притягиваются, поэтому разносить их на большие расстояния энергетически невыгодно — ведь для этого надо преодолевать энергию их притяжения. Если температура кристалла мала и не может преодолеть этот энергетический барьер, пара близких монополей может спокойно существовать не исчезая.

Рис. 6. Другая возможность для устранения «неубиваемых» монополей — синхронный переворот стрелочек сразу в целом квадратном блоке (сначала в квадрате 1, затем в квадратах 2 и 3). На каждом шаге цепочка неправильных стрелочек укорачивается
Впрочем, расплетание пары монополей — не единственный способ укоротить цепочку неправильных спинов. Это можно сделать, вообще не трогая монополи, а лишь синхронным образом переворачивая сразу несколько стрелочек. На рис. 4 есть квадратный блок, в котором четыре стрелочки образуют замкнутую линию. Если все направления стрелочек в этом блоке развернуть, то никаких новых монополей мы не создадим, зато цепочка неправильных спинов укоротится. Проделав такую процедуру три раза (стадии 1-2-3 на рис. 6), мы укоротим цепочку до минимума, и уже тогда пара сможет легко проаннигилировать. Проблема тут только в том, что при низкой температуре этот процесс очень маловероятен. Ведь мы не можем в квадратном блоке поворачивать стрелочки одну за другой — это привело бы к новым монополям, а значит, потребовало бы затрат энергии. Эти четыре стрелочки должны развернуться одновременно и синхронно. В реальных ситуациях при низких температурах такие многочастичные синхронные процессы практически исключены.
Описанное свойство монополей очень важно для экспериментального изучения этих образований в спиновом льду. В эксперименте удается создать достаточно большую концентрацию этих монополей, которые, разумеется, будут притягиваться друг к другу. Если бы это сближение всегда заканчивалось аннигиляцией, «монопольный газ» был бы очень недолговечной системой, и с ним трудно было бы проводить эксперименты. Но, к счастью, уничтожить пару монополей можно только после того, как соединяющая их цепочка неправильных спинов-стрелочек сократится до кратчайшего пути. Пока она остается длинной — пара монополей неубиваема. Поэтому газ монополей вполне может разбиться на пары, внутри каждой пары монополи будут держаться вместе за счет притяжения, но при этом избегают взаимного уничтожения. Получается необычное состояние вещества, стабильность которого обеспечивается именно длинными переплетенными цепочками неправильных спинов, которые как-то проложили себе путь по кристаллу. Изучение этого состояния вещества — само по себе интересная физическая задача.
Для полноты картины стоит еще подчеркнуть, что для монополей в реальном спиновом льду всё же имеется отличие между настоящей трехмерной решеткой и двумерной квадратной решеткой, которую мы использовали в этой задаче. В трехмерной решетке все четыре стрелки, подходящие к выбранному узлу, расположены совершенно одинаково относительно друг друга. В двумерной эта симметрия нарушается: у каждой стрелки есть два ближайших соседа и один дальний. В реальных ситуациях от этого меняется энергия взаимодействия электронов, и тогда описание решетки усложняется.

Рис. 7. Пример магнитного состояния в плоской квадратной решетке в искусственном спиновом льду. Вверху показана общая картина, внизу — несколько отдельных узлов и соответствующие им ориентации стрелочек. Цветом показано локальное магнитное поле в образце. Изображение из статьи J. P. Morgan et al., 2011. Thermal ground-state ordering and elementary excitations in artificial magnetic square ice
Монополи в таком случае тоже могут существовать, но связывающие их цепочки перевернутых спинов уже сами обладают энергией, причем, чем длиннее цепочка, тем эта энергия больше. Это приводит к силе упругости цепочки и сильно влияет на поведение монополей в такой системе: они уже не столь свободны, как в нашей задаче. Такие системы изучались экспериментально, но, правда, здесь речь шла не про настоящую кристаллическую решетку с электронами, а про «искусственный кристалл» — большой массив из наноразмерных магнитиков (рис. 7). Подробнее об этой системе можно почитать в недавней обзорной статье.
Последние задачи













Рис. 1. В некоторых материалах при низких температурах существуют особые электронные дефекты, похожие на магнитные монополи. Рисунок из статьи C. Castelnovo et al., 2007. Magnetic monopoles in spin ice