Выборы, выборы

В этой задаче требуется посчитать некоторое число способов. Это — типичный вопрос для комбинаторики. И, как это обычно бывает в этом разделе математики, ценен не столько ответ на одну конкретную задачу, сколько рецепт (если он, конечно, есть) получения ответов для всех подобных задач. Такой подход можно применить и здесь. Посмотрите, что происходит в аналогичной ситуации, когда проголосовало 2, 4, 6 и т. д. человек (поскольку кандидаты получают равное число голосов, то в урне должно быть четное число бюллетеней), и как связаны между собой ответы в этих случаях.

Пусть кандидатов зовут А и Б, и при подсчете А должен всё время не уступать Б по количеству голосов. Бюллетени будем обозначать именами кандидатов. Тогда любую стопку из условия можно записать в виде «слова» из букв А и Б. (Важно, что в этот момент мы забываем различия между бюллетенями: если избиратели Иванов и Петров оба проголосовали за одного кандидата, то, по идее, поменяв их бюллетени в стопке местами, получим новую стопку. Но сейчас мы не обращаем внимание на то, чей бюллетень лежит выше, а посчитаем ответ по модулю таких перестановок. Потом нужно будет не забыть умножить результат на некоторый множитель.) Итак, нам подходят стопки, в которых А ни в какой момент не уступает Б; такие стопки (и соответствующие им слова) будем называть правильными. Пусть в голосовании участвовало 2n избирателей, и за каждого кандидата было отдано по n голосов. Число правильных стопок в этой ситуации обозначим C_n. Дальше мы найдем явное выражение для C_n через n и, как следствие, вычислим C₅₀. При этом удобнее будет говорить про слова, а не про стопки, поэтому будем считать их (хотя это одно и то же).

Посмотрим, что происходит при небольших n. Если n = 1, то есть только одно правильное слово — АБ (второе возможное слово БА, очевидно, неправильное). Если n = 2, то правильных слов два: ААББ и АБАБ. Если n = 3, то таких слов уже пять: АААБББ, ААББАБ, ААБАББ, АБААББ и АБАБАБ. Уже сейчас можно заметить принцип, по которому длинные правильные слова «распадаются» на короткие: каждое правильное слово w единственным образом представляется в виде w = Аw₁Бw₂, где на месте w₁ и w₂ стоят более короткие правильные слова (возможно, одно из них пустое), суммарная длина которых на 2 меньше длины слова w. Это наблюдение позволяет сразу же выписать рекуррентную (то есть выражающую элемент последовательности через предыдущие) формулу для C_n:

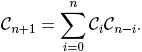
Здесь мы полагаем, что C₀ = 1. Почему формула такая? Первое слагаемое суммы в правой части — C₀C_n — отвечает случаю, когда w₁ — пустое слово, а w₂ — слово длины 2n. Остальные слагаемые получаются аналогично.

Эта формула уже позволяет вычислить то, что нам нужно: используя ее можно последовательно найти C₄, C₅, и т. д. Но мы пойдем дальше и найдем более удобное выражение для C_n.

Для этого придется рассмотреть не только правильные, а вообще все слова длины 2n, в которых буквы А и Б встречаются по n раз. Отметим, что другие слова мы в принципе не рассматриваем, ограничиваясь только таким (странным) словарем. Обозначим их количество за . Тогда , так как каждое такое слово однозначно определяется теми местами, на которых будут стоять буквы А, то есть слов столько же, сколько способов выбрать n мест из 2n возможных, а это и есть число сочетаний из 2n по n (напомним, что n! = 1 · 2 · ... · n — факториал числа n).

Но можно найти и другим способом, через рекуррентное соотношение, по аналогии с формулой для C_n. Опять же, заметим, что любое слово w представляется в либо в виде w = AuБw₁ (где слово u — правильное, а слово w₁ — произвольное), либо в виде w = БАw₁ (где слово получается из некоторого правильного заменой всех букв А на буквы Б и наоборот, а слово w₁ — произвольное). Доказательство того, что это верно, то есть что любое слово можно представить однозначно в таком виде, не слишком сложное и остается в качестве упражнения. Отсюда

Далее, любое неправильное слово начинается с правильного куска (который может быть пустым), после которого стоит буква Б, а в оставшейся части — «хвосте» — букв А на одну больше, чем букв Б. Разных «хвостов» длины 2k + 1 есть . Это число равно . Поэтому всего неправильных слов длины 2(n + 1) будет . С другой стороны, число неправильных слов равно числу всех слов минус число правильных слов, то есть .

Теперь, так как число правильных слов равно числу всех слов минус число неправильных слов, то

Сравнивая это выражение с самой первой рекуррентной формулой, делаем вывод, что для всех i. Это и дает окончательную формулу:

Применяя ее, получаем, что C₅₀ = 1 978 261 657 756 160 653 623 774 456.

Теперь вспоним, что надо еще учесть все возможные перекладывания бюллетеней в стопке, которые не поменяют порядок голосов за кандидатов. То есть можно представить себе, что мы вынимаем из стопки все бюллетени за одного кандидата, тасуем их, а потом возвращаем назад, чтобы сохранился исходный порядок голосов. Ясно, что если это учитывать, то каждая стопка «породит» еще 50! вариантов при тасовании по любому из кандидатов. Значит, нужно умножить всё на (50!)², чтобы получить окончательный ответ:

1 829 925 793 018 512 797 680 377 232 475 817 656 680 705 260 085 914 146 442 999 292 063 090 195 945 684 619 783 165 960 316 794 476 201 052 900 408 376 936 436 297 749 233 664 000 000 000 000 000 000 000 000.

Казалось бы, всего 100 бюллетеней, а сколько получается вариантов...

Последовательность, для которой мы нашли формулы и вычислили несколько первых и сотый элементы, называется последовательностью чисел Каталана. Так получается, что она возникает как ответ во многих перечислительных задачах, которые, на первый взгляд, совсем разные. Мы уже видели, что ее члены являются ответами на вопросы о количестве стопок бюллетеней и слов с заданными свойствами (правда, тут и без ремарки в решении довольно понятно, что речь идет про одно и то же). Также довольно очевидно, что столько же будет и правильных скобочных структур из 2n скобок: скобочная структура — запись только из открывающих и закрывающих скобок — называется правильной, если и тех, и других скобок поровну и в любом начальном куске открывающих скобок не меньше, чем закрывающих. Каталан как раз и открыл связи последовательности с задачей о перечислении скобочных структур, поэтому последовательность носит его имя.

А вот если нужно посчитать число двоичных деревьев с n ребрами (дерево называется двоичным, если у каждого узла не более двух потомков)? Или число путей в клетчатом квадрате n × n, которые идут из угла в противоположный по линиям сетки и не пересекают диагональ квадрата (на рисунке показаны все 14 таких путей для n = 4)?

Или число разрезаний правильного (n + 2)-угольника на n треугольников? Как вы уже поняли, во всех этих и многих других задачах ответ тот же самый. Каждую из таких задач можно свести к другой. В качестве примера покажем, как построить правильную скобочную структуру по бинарному дереву. Считаем, что оно нарисовано на бумаге, и представим себе муравья, который ползет вокруг этого дерева, стартовав от корня. Когда муравей проползает мимо очередного ребра в первый раз, нужно поставить открывающую скобку, когда он ползет мимо ребра второй раз с другой стороны, то нужно поставить закрывающую. В итоге когда наш воображаемый муравей вернется к месту старта, то будет выписана скобочная структура, соответствующая данному дереву. Можно показать, что такое соответствие взаимно однозначно и поэтому деревьев столько же, сколько и скобочных структур.

Можно рассмотреть более общую ситуацию: на участок пришло p + q избирателей, из них p отдают свой голос за первого кандидата, а q — за второго. Это было сделано во второй половине XIX века несколькими учеными, в честь одного из которых это называется проблемой Бертрана о выборах. Правда, вопрос они ставили несколько иначе: их интересовало, с какой вероятностью первый кандидат при подсчете голосов будет всегда опережать второго? Ответ оказался на удивление прост: (p – q)/(p + q). Да и обоснование этого ответа не слишком сложное. Но к нашей задаче, конечно, ближе немного другой вопрос: с какой вероятностью при подсчете голосов первый кандидат ни в какой момент не будет уступать второму? Здесь ответ такой: (p – q + 1)/(p + 1). Это отлично согласуется с формулами из решения (при p = q = n как раз получается вероятность 1/(n + 1)). С простым и наглядным доказательством этого факта можно познакомиться здесь.