Окружность и линейка

На данной окружности с помощью двусторонней линейки легко построить вершины равнобедренной трапеции. Вспомните, что серединный перпендикуляр к любой хорде проходит через центр окружности. Подумайте, как, применяя эти факты, построить центр окружности.

В основе решения лежат две теоремы школьной геометрии:

Теорема 1. В равнобедренной трапеции следующие 4 точки лежат на одной прямой, перпендикулярной основаниям: середины обоих оснований трапеции, точка пересечения диагоналей и точка пересечения прямых, содержащих боковые стороны (рис. 2, слева).

Рис. 2.

Теорема 2. Серединный перпендикуляр к хорде окружности проходит через центр этой окружности (рис. 2, справа).

Теорему 1 иногда называют замечательным свойством трапеции.

Рис. 3.

Теперь можно приступать к построению, которое мы проведем пошагово. Приложим линейку так, чтобы обе ее стороны пересекали окружность (рис. 3). Это можно сделать, потому что ширина \(h\) линейки меньше радиуса \(R\) окружности по условию задачи. Проведем две параллельные прямые, «обведя» стороны линейки. Пусть эти прямые пересекают окружность в четырех точках \(A\), \(B\), \(C\) и \(D\). Эти точки являются вершинами равнобедренной трапеции \(ABCD\). Равнобедренная она потому, что параллельные прямые высекают на окружности равные дуги, значит, стягивающие их концы хорды тоже равны.

В трапеции \(ABCD\) продолжим боковые стороны \(AB\) и \(CD\) до пересечения в точке \(K\) (рис. 4) и проведем прямые, содержащие диагонали \(AC\) и \(BD\), которые пересекаются в точке \(F\). Через точки \(K\) и \(F\) проведем прямую \(n\) (красного цвета), которая, согласно теореме 1, проходит через середины оснований, перпендикулярно им. Но тогда, согласно теореме 2, серединный перпендикуляр \(KF\) к хорде \(AD\) проходит через центр окружности.

Рис. 4.

Если повторить все эти построения с другой парой параллельных прямых, не параллельных первой паре, получим вторую прямую \(m\) (синего цвета), проходящую через центр окружности. Понятно, что точка пересечения прямых \(n\) и \(m\) является центром данной окружности (рис. 5).

Рис. 5.

Описанное построение центра окружности предложил В. Казаков.

Эта задача публиковалась на сайте diofant.ru. Специфика сайта такова, что решившие задачу участники должны вводить числовой ответ. Но какой числовой ответ можно вводить при решении задач на построение? Модераторы в качестве числовой характеристики решения взяли количество операций, выполнение которых приводит к построению центра окружности. При этом за одну операцию считается приложение линейки к рисунку и проведение либо одной прямой, либо пары параллельных прямых с обеих сторон линейки.

Задача 2667. Имеются двусторонняя линейка и окружность, радиус которой больше ширины линейки. За одну операцию можно либо провести прямую, либо провести две параллельные прямые, используя обе стороны линейки. За какое минимальное количество операций можно найти центр окружности?

В приведенном решении для построения красной прямой \(n\) требуется 6 операций. Еще 6 операций выполнено при построении синей прямой \(m\). Таким образом, центр окружности найден при помощи 12 операций. Именно это число было заложено в систему для проверки ответов, присылаемых решателями. Впоследствии ответ в этой задаче неоднократно менялся, потому что решатели находили все более короткие решения. А поиск самого короткого решения захватил всех, как в хорошем детективе. Вот об этом и пойдет речь ниже.

Первое, что пришло в голову многим решателем, — более экономное (по сравнению с описанным в решении) построение прямой, проходящей через центр окружности. Напомним, что линейка один раз на первом этапе использовалась как двусторонняя и далее пять раз как односторонняя. Здесь экономия операций заключается в совмещении, точнее, в одновременном применении обоих приемов и одновременном построении прямых \(m\) и \(n\).

А именно: при построении первой прямой \(n\), когда проводится диагональ \(BD\), по второй стороне линейки можно провести прямую \(AE\) (рис. 6, слева). Далее продолжается построение прямой \(n\), но уже подготовлена трапеция \(ABDE\) для построения второй прямой \(m\). Так можно сэкономить одну операцию. Более того, при дальнейшем построении второй прямой \(m\) экономится ещё одна операция: не надо проводить прямую \(AB\) (рис. 6, справа), поскольку она уже проведена, ведь трапеции \(ABCD\) и \(ABDE\) имеют общую боковую сторону \(AB\). Получается, что при этом построении экономится 2 операции и ответ в задаче становится равным 10.

Рис. 6.

Следующей находкой был более эффективный прием построения прямой, содержащей диаметр окружности. Он тоже начинается с построения вершин равнобедренной трапеции \(ABCD\), но далее можно обойтись без проведения прямых, содержащих боковые стороны. Вместо этого, проводя диагонали трапеции, строим сразу две пары параллельных прямых, которые пересекаются в точках \(K\) и \(F\), задающих прямую \(n\), проходящую через центр окружности. При этом сделано четыре операции, значит, повторив их дважды, можно построить вторую прямую, проходящую через центр окружности. Тогда задача решается за 8 операций. Но, как и в предыдущем случае, имея уже построенную ранее трапецию, можно сэкономить одну операцию и решить задачу за 7 операций.

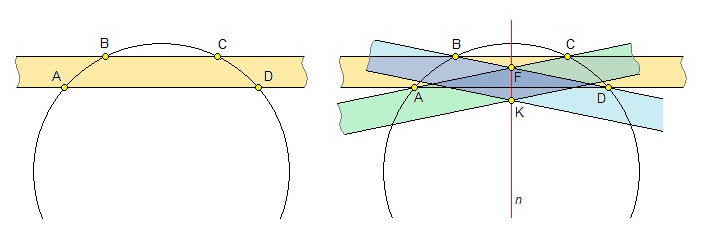
Рис. 7.

Конструкцию, полученную за 4 операции (рис. 7, справа), можно продолжить иначе, если во время 4-й операции вместе с прямой \(n\) провести и прямую \(m\parallel n\), а 5-й операцией провести прямую \(p\parallel n\). Так мы получим две прямые, равноотстоящие от прямой \(n\). Поскольку \(n\) проходит через центр окружности, прямые \(m\) и \(p\), пересекаясь с окружностью, задают вершины прямоугольника \(MLNP\) (рис. 8). Проведя его диагональ \(MN\) — 6-я операция, — получим центр окружности \(O\) как точку пересечения этой диагонали с прямой \(n\). Центр построен за 6 операций.

Рис. 8.

Соревнуясь в поиске самого короткого построения центра окружности, решатели придумали прием построения прямой, содержащей диаметр окружности, всего за три операции. Основан он на том, что через две заданные на окружности точки \(A\) и \(B\) можно провести пару параллельных прямых так, что точки \(A\) и \(B\) лежат на разных прямых, причем сделать это можно двумя различными способами. Проделав это, получим ромб \(AKBF\), вершины \(A\) и \(B\) которого лежат на окружности (рис. 9, слева). Вспомнив, что диагонали ромба взаимно перпендикулярны, получим, что прямая \(KF\) является серединным перпендикуляром к хорде \(AB\). Значит, прямая \(KF\) проходит через центр окружности.

Рис. 9.

Проделав такие же построения для точек \(B\) и \(C\), получим прямую \(m\), проходящую через центр окружности (рис. 9, справа). Точка O пересечения прямых \(n\) и \(m\) является центром окружности. При таком построении выполнено 5 операций.

Казалось бы, улучшать уже некуда? Ан нет! Было найдено решение задачи за 4 операции (рис. 10):
    1) На данной окружности отметим две точки \(A\) и \(B\), расстояние между которыми больше ширины линейки;
    2) Построим две пары параллельных прямых, проходящих через точки \(A\) и \(B\). На рисунке эти операции обозначены цифрами 1 и 2. При пересечении полос 1 и 2 образовался ромб, диагональю которого является отрезок \(AB\). Другая пара вершин \(K\) и \(F\) этого ромба определяет прямую \(n\) (красную), перпендикулярную \(AB\), значит, прямая \(n\) проходит через центр окружности;
    3) Проведем прямую \(n\) и параллельную ей прямую. На рис. 10 это полоса 3 и операция 3. Прямые третьей полосы на окружности задают точки \(C\) и \(D\), отметим их;
    4) Проведем еще одну пару прямых, проходящих через точки \(C\) и \(D\). На рисунке это полоса 4 и операция 4. При этом прямая \(m\), проходящая через точку \(C\), проходит через центр окружности, значит, точка пересечения прямых \(n\) и \(m\) является центром окружности.

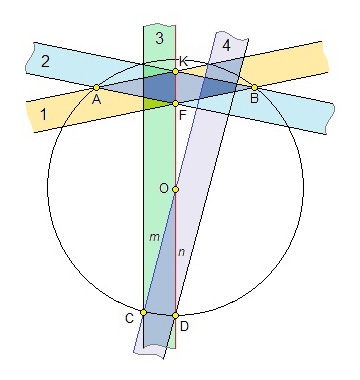
Рис. 10.

Вот такая история получилась при поиске самого короткого построения центра окружности двусторонней линейкой. Учитывая, что все это происходило в атмосфере соревновательности, где правильные решения поощряются 100-бальной оценкой, а неправильные решения наказываются штрафными очками, напряжение «висело» две недели. Сейчас на сайте diofant.ru всё успокоилось, участники получили свои баллы и уже решают другие задачи, а задача на построение центра окружности осталась с ответом в 4 операции. Но как долго этот ответ будет актуальным? Все изменится, если кто-то найдет построение за три операции, ведь до сих пор не доказано, что построение за 4 операции самое короткое.