Экономика звездной пыли

В пунктах а) и б) подумайте, есть ли компании смысл не тратить часть денег? Как найти максимум данной функции на каком-либо промежутке?

в) На самом деле, при любом соотношении цен каждая из компаний решает свою задачу, полностью аналогичную первым двум пунктам (что будет соответствовать количеству денег?). А что нужно, чтобы обмен состоялся? На всякий случай заметим, что мы считаем, что компании договорились о курсе, если при данном соотношении цен селена и теллура «Альдебаран» хочет продать ровно столько теллура и купить ровно столько селена, сколько «Бетельгейзе» хочет этих элементов, соответственно, купить и продать.

«Из общих соображений» (обсудим это в послесловии) ясно, что компания потратит все деньги. Ведь чем больше денег потратишь, тем больше ресурсов получишь и тем больше звездной пыли произведешь, а значит прибыль тоже будет больше. Тогда получается, что количество селена, которое приобретет компания, располагающая ресурсами \(R\), можно (при ценах \(p\), \(v\)) найти так:

И после этого надо просто найти такое значение переменной \(t\) (вообще говоря, такое неотрицательное значение), что значение функции \(SD(t)\) будет максимальным.

Для «Альдебаран Лимитед»:

Это квадратичная функция, максимум достигается в вершине соответствующей параболы. Получаем:

Для «Бетельгейзе Анлимитед»:

Это кубическая функция, и чтобы найти ее максимум, придется найти нули производной (разумеется, то же можно было сделать и в случае «Альдебаран Лимитед», но там это было не нужно — вершину параболы можно найти и без производной).

Видно, что производная равна нулю или когда \(t=0\) (этот случай нам не интересен по смыслу, к тому же, это минимум), или когда

Если вдруг вы не могли решить пункт в), потому что не понимали, как решать первые два пункта, то попробуйте порешать сейчас. Для удобства, считайте, что цена селена \(p = 1\), а теллура — \(v\). Так как в задаче спрашивалось про обменный курс, это как раз то, что нужно. Решение пункта в) откроется по нажатию на слова ниже.

Задачи, похожие на рассмотренную нами, называются оптимизационными: с точки зрения здравого смысла, мы ищем лучшее действие в некоторой ситуации, а с точки зрения математики — ищем наибольшее (иногда наименьшее, но это не важно) значение функции на заданной области. Математические методы оптимизации — из важнейших инструментов экономики, ведь доступные ресурсы чаще всего ограничены (как селен и теллур в нашей задаче).

Например, пункт а) с точки зрения математики — это максимизация произведения двух величин, \( s \times t \rightarrow \max\), на данной области:

Для решения оптимизационных задач с ограничениями в виде неравенств применяют, например, метод Куна — Таккера. Но, как мы и сказали в решении, очевидно, что компания потратит все имеющиеся у нее ресурсы. И действительно, предположим, что немного денег осталось. Но мы знаем, что, потратив их в любой пропорции на селен и теллур, компания увеличит количество произведенной звездной пыли (а значит, и прибыль). Математически это следует из того, что производная производственной функции по обеим переменным строго положительна, хотя интуитивно понятно без всякой математики. Так задача превращается в задачу с ограничениями в виде равенства. В общем случае для решения пришлось бы использовать метод множителей Лагранжа, но мы-то решаем задачу, где переменных всего две, да и ограничение линейное. Так что можно просто выразить одну переменную через другую, как мы и сделали в решении выше. Но интересно подумать, в чем смысл точки, которую мы найдем.

Если рассуждать геометрически, то выпуск продукции (звездной пыли) не меняется при движении по линии, заданной уравнением \( st=С\) (такая кривая называется равнобочной гиперболой). При этом мы хотим сделать \(C\) большим, но не можем выйти за пределы допустимой области — области, ограниченной линией \( ps+vt=R \). Это прямая с отрицательным градиентом (если, конечно, мы считаем цены положительными) и, как хорошо видно на рис. 1, при увеличении \(C\) в какой-то момент гипербола просто перестает пересекаться с областью. Последняя гипербола, имеющая общую точку с областью (эта точка лежит на границе, как мы обсудили в предыдущем абзаце), касается и этой прямой.

Рис. 1.

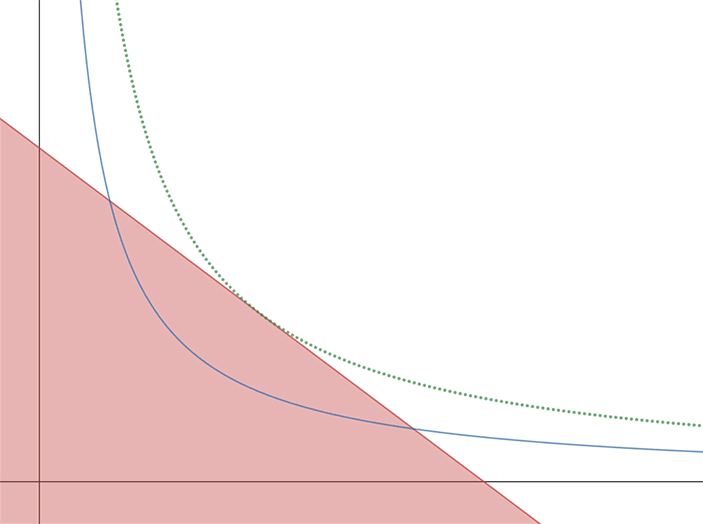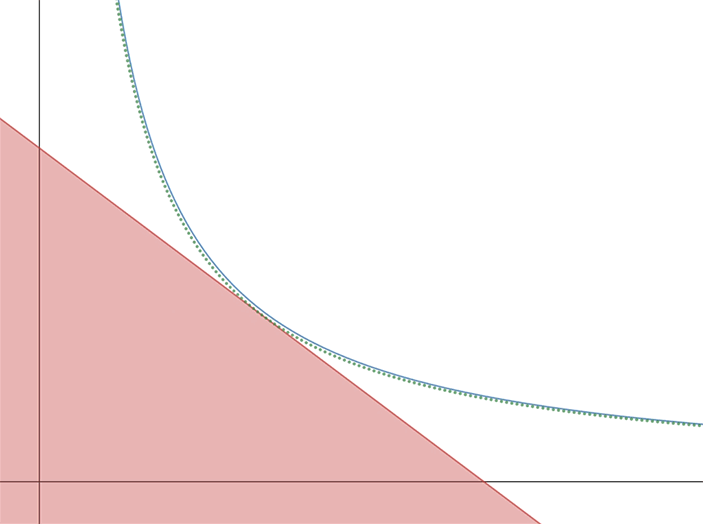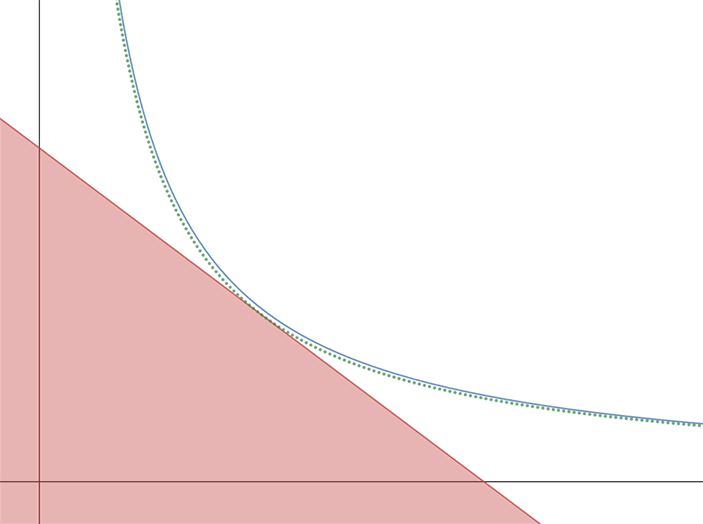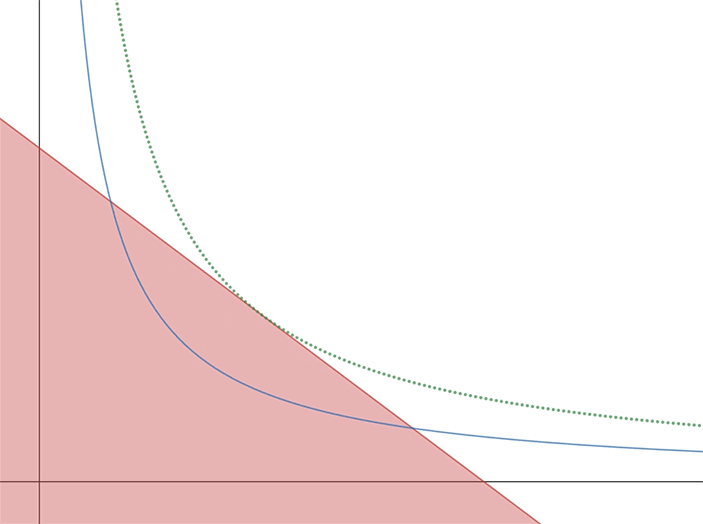
В чем же экономический смысл касания? Из математики мы знаем, что раз прямая касается гиперболы, то производная \( \mathrm{d}t(s)/\mathrm{d}s\) гиперболы в этой точке будет равна угловому коэффициенту прямой. Производная — это отношение бесконечно малого изменения функции к бесконечно малому изменению аргумента, но в нашем случае \(t\) — не совсем функция, это второй ингредиент производства, то есть производная показывает, как соотносятся изменения (пускай очень малые) ресурсов при условии сохранения выпуска (в экономике это называется предельной нормой замещения). А угловой коэффициент прямой — это соотношение цен (строго говоря, с минусом, но это компенсируется тем, что изменения \(s\) и \(t\) разнонаправленны). То есть максимально эффективно распределять ресурсы так, чтобы эти соотношения совпадали. Что же это означает? Если не думать о математической строгости, то единица селена приносит столько же прибыли, сколько \(p/v\) единиц теллура. Но и стоит единица селена как \(p/v\) единиц теллура. Получается, что в оптимальной точке условная единица денег принесет одинаковую прибыль, независимо от того, в какой из ресурсов ее вложить.

Проверку того, что все сказанное здесь, выполняется для точек, найденных в решении пунктов а) и б) оставим как простое упражнение. Кстати, обе производственные функции (\(SD_{A} = st\) и \(SD_{B}=st^2\)) — частные случаи функции Кобба — Дугласа, нередко используемой для описания производства с двумя факторами, в особенности с трудом и капиталом. Так, функцию Кобба — Дугласа часто используют как пример, удовлетворяющий условиям одной из классических моделей экономического роста, модели Солоу.

Но что же происходит в пункте в), когда две компании должны договориться об обменном курсе? Здесь, конечно, нужно сделать много оговорок. Например, почему компании вообще решили обмениваться ресурсами? О том, что могло бы быть, если отдать все ресурсы одной (более эффективной, а в данном случае, «Бетельгейзе Анлимитед» умеет из того же объема ресурсов производить больше звездной пыли) мы здесь говорить не будем, так что будем считать, что «по условию задачи». А что означает, что компании договорились? Про это было сказано в подсказке 2: мы считаем, что это курс, когда спрос на селен (на самом деле, на оба ресурса, — об этом чуть ниже) равен предложению. Почему так? Предположим, что компании договорились о курсе обмена 1 к 1 (единицу селена можно поменять на единицу теллура). Как мы знаем из первых двух пунктов, в этом случае «Альдебаран Лимитед» хочет иметь равные количества селена и теллура, то есть предложит поменять 1800 единиц своего теллура на столько же селена. Но «Бетельгейзе Анлимитед» в этих условиях хочет иметь в два раза больше теллура, чем селена, и захочет поменять 1600 единиц своего селена на 1600 единиц теллура. Получается, что на «рынке» недостаток селена (его нужно \(1800 + 800 = 2600\), а есть только 2400) и избыток теллура (нужно \(1800 + 1600 = 3400\), а есть 3600). Как при этом договариваться об обмене, не очень ясно.

Ситуацию, в которой — при данных ценах — у каждого участника рынка лучшая из возможных (с его точки зрения) комбинация товаров, а спрос на любой товар равен предложению, называют равновесием по Вальрасу (Walrasian equilibrium). А Закон Вальраса говорит о том, что, если на рынке из \(n\) товаров спрос на каждый из \(n-1\) товара равен предложению, то же будет и с последним товаром. В нашем случае это означает, что второе уравнение в системе, приведенной в решении, было лишним — мы обнаружили это опытным путем, но на самом деле, так будет всегда.

Попробуем посмотреть на геометрический смысл обмена. Для этого используем ящик Эджворта — диаграмму, которая показывает распределение двух ресурсов между двумя участниками рынка. В нем количество товара у первого участника показывается на обычных координатах (левая вертикальная и нижняя горизонтальная линии), а у второго — наоборот (правая вертикальная и верхняя горизонтальная линии, причем увеличиваются значения на этих осях тоже в направлениях противоположных обычным). Если длины отрезков осей сделать равными общему количеству соответствующего товара, то любая точка внутри прямоугольника будет соответствовать некоторому распределению ресурсов. На рис. 2 красным показаны оси и ресурсы «Бетельгейзе Анлимитед», а зеленым — ресурсы «Альдебаран Лимитед». При этом изначально рынок находится в правом нижнем углу.

Рис. 2.

Если компании договорились о курсе обмена, то оказывается, что, обменявшись каким-то количеством товара, они могут оказаться в любой точке ящика, лежащей на прямой, градиент которой — это соотношение цен. Прямая должна проходить через изначальное положение (распределение ресурсов), и потому однозначно определена курсом. Как мы уже знаем, при любом курсе каждая компания попытается выбрать такую точку, в которой линия уровня функции производительности коснется прямой обмена. В нашем случае кривые для «Бетельгейзе» будут идти «в другую сторону» (ведь у них перевернутый график). На рис. 3 показаны точки, которые компании хотели бы выбрать при разных курсах. А ситуацией равновесия (по Вальрасу), которую мы и просили найти в задаче, будет случай, когда точки A и B совпадут. В этом случае прямая обмена будет одновременно касательной к графикам обеих производственных функций, которые в этой точке касаются друг друга. А предельная норма замещения в этот момент одинакова для обеих компаний.

Рис. 3.

Интересно посмотреть, что будет, если изначальное распределение ресурсов другое. Решение задачи будет точно таким же: через начальную точку в ящике Эджворта нужно будет провести все возможные прямые и найти ту, которая коснется линий уровня обеих производственных функций одновременно. Несколько таких точек показаны на рис 4.

Рис. 4.

На самом деле, в нашей ситуации (выпуклых вниз производственных функций) любая линия уровня одной фирмы коснется какой-то линии уровня другой. А все точки касания образуют так называемую договорную кривую (contract curve). Это те распределения ресурсов, в которых будет достигаться равновесие при разных начальных точках. Все эти точки обладают еще одним интересным свойством — такие распределения называются Парето-оптимальными. Это значит, что нельзя сделать лучше кому-то, не сделав хуже другому. Это достаточно важное понятие, потому что из Парето-оптимальной точки сложно куда-нибудь сдвинуться. Допустим, государство хочет сделать лучше жизнь пенсионеров, но, чтобы ее улучшить, нужно повысить налоги, то есть ухудшить ситуацию для тех, кто их платит. Или, например, мэр хочет построить велодорожки, но это ухудшает ситуацию для автомобилистов. Поэтому многие ситуации, которые в целом не очень удачные (например, несправедливые) могут держаться достаточно долго: даже если понятно, что кому-то слишком хорошо относительно других, может быть не так просто смириться с тем, что надо сделать этому кому-то хуже. Заметим, что экономика помогает оценить, кто выигрывает в той или иной ситуации, но не отвечает на вопрос «как надо?».

Но если вдруг кажется, что все ситуации такие, и никогда нельзя улучшить ситуацию для кого-то, не ухудшив для другого — это большое заблуждение. И пример с теллуром и селеном отлично его иллюстрирует: от ситуации, где ни одна компания не могла произвести вообще ничего, компании, просто договорившись о курсе обмена, перешли к тому, что каждая произведет достаточно много звездной пыли и получит прибыль.

Автор благодарит создателей сайта desmos.com и очень рекомендует его в качестве инструмента для построения графиков.