Рамки из домино
Задача

В стандартном комплекте домино 28 костяшек. Каждая костяшка — это прямоугольник 2×1, составленный из двух единичных квадратиков, в которых написано по числу от 0 до 6. Всего разных пар с этими числами существует ровно 28 — как раз по числу костяшек.
Можно ли выложить весь комплект в виде фигуры, состоящей из пяти квадратных рамок (рис. 1), чтобы при этом у соседних костяшек на соприкасающихся половинках были одинаковые числа, а суммы чисел в рамках были одинаковыми?
Подсказка
Чему должна быть равна сумма чисел в каждой из пяти рамок? А чему равна сумма четырех чисел, находящихся в общих клетках квадратных рамок?
Решение
Заметим, что центральная рамка не может быть составлена из шести костей домино, потому что тогда, например, верхняя слева рамка не складывается, ведь в ней остается нечетное число клеток.
В данной фигуре есть четыре клетки, каждая из которых принадлежит двум рамкам. Будем называть их узловыми. Обозначим четыре числа, расположенные в узловых клетках, буквами a, b, c и d (рис. 2, слева), а сумму всех 12 чисел в каждой из рамок обозначим через S (по условию суммы во всех рамках равны друг другу). С учетом основного правила домино остальные числа центральной рамки могут располагаться только так, как показано справа на рис. 2, поэтому получаем уравнение \(3(a+b+c+d)=S\).

Рис. 2.
Учитывая, что сумма чисел на всех костяшках домино равна 168, составим еще одно уравнение: \(5S-(a+b+c+d)=168\). Решая систему этих двух уравнений, находим \(a+b+c+d=12\) и \(S=36\).
Если взять, например, четверку чисел \(a=0\), \(b=2\), \(c=4\), \(d=6\), то моментально определяются четыре косточки центральной рамки (рис. 3, слева). Остальные 24 костяшки нетрудно разбить на четыре группы по шесть костяшек так, чтобы в каждой группе можно было, во-первых, сложить рамку по правилам домино, во-вторых, сумма чисел в ней равнялась 36. Одно из решений приведено на справа на рис. 3.
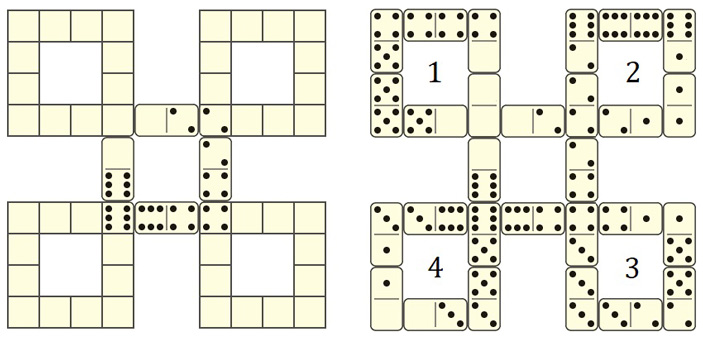
Рис. 3.
Заметим, что из этого решения можно получить другие варианты, манипулируя с угловыми квадратными рамками или их фрагментами. Перечислим эти манипуляции:
- отразить рамку симметрично относительно диагонали, содержащей узловую клетку;
- «прокрутить» рамку, переставив костяшки домино в том же порядке, но поставив на узловую клетку другую костяшку с тем же числом;
- поменять местами угловые рамки, сохранив значения в узловых клетках, сделав соответствующую «прокрутку» рамок. Например, в приведенном решении порядок угловых рамок (1234) можно заменить на порядок (4312);
- изменить направление фрагмента из нескольких костяшек на противоположное, например, в угловой рамке №4 фрагмент (3–1)(1–0)(0–3) из трех костяшек можно расположить в противоположном направлении (3–0)(0–1)(1–3).
Все новые варианты, полученные такими манипуляциями, не будем считать существенно различными решениями. Все остальные расстановки будем считать существенно различными. Поиск всех существенно различных решений с помощью компьютера провел Тальмон Сильвер из Израиля. Он выяснил, что рассмотренная нами четверка узловых чисел (0, 2, 4, 6) позволяет получить два существенно различных решений нашей задачи.
Он же провел анализ всевозможных четверок узловых чисел и для каждой из них выяснил количество существенно различных решений задачи. Все его результаты приведены в таблице:
| Четверка | Число решений | Четверка | Число решений |
| (0,1,5,6) | 4 | (1,1,4,6) | 10 |
| (0,1,6,5) | 10 | (1,2,3,6) | 1 |
| (0,2,4,6) | 2 | (1,2,4,5) | 0 |
| (0,2,5,5) | 10 | (1,2,5,4) | 8 |
| (0,2,6,4) | 8 | (1,2,6,3) | 3 |
| (0,3,3,6) | 2 | (1,3,2,6) | 3 |
| (0,3,4,5) | 1 | (1,3,3,5) | 6 |
| (0,3,5,4) | 3 | (1,3,4,4) | 12 |
| (0,4,2,6) | 2 | (1,4,2,5) | 6 |
| (0,4,3,5) | 3 | (2,2,3,5) | 12 |
| (0,5,1,6) | 0 | (2,3,3,4) | 0 |
Таким образом, задача имеет 102 существенно различных решения. Если же различать решения только по четверке узловых чисел, то будет всего 19 решений. Если же вообще не делать никаких ограничений, то число решений задачи огромно! Посчитает ли кто-нибудь?
Послесловие

Рис. 4.
Если внимательно посмотреть на предложенное в решении расположение костяшек домино, то можно заметить, что все они выложены вдоль замкнутой самопересекающейся линии, изображенной на рис. 4.
Пользуясь тем, что костяшки выложены по правилам домино, можно избавиться от «петлеобразности» этой линии и трансформировать ее в квадрат. На рисунках 5 и 6 показано, как, перекладывая костяшки в найденном нами решении, поэтапно преобразовать фигуру из пяти рамок 4×4 в одну большую квадратную рамку. Сначала нужно «вывернуть» левую полупетлю, ограничивающую рамки №1 и №4, потом проделать то же самое с правой полупетлей, ограничивающей рамки №2 и №3. Теперь сдвинем все домино к центру, чтобы исчезли пробелы между домино: получится фигура в виде гантели, показанная на рис. 5 справа.

Рис. 5.
Из этой «гантели» легко получить крестообразную фигуру, показанную слева на рис. 6. Осталось вывернуть ее углы и получить большую квадратную рамку 15×15. Справа на рис. 6 она показана вместе с соответствующим решением с рис. 3.

Рис. 6.
Сравним расположение четырех костяшек, образующих основу центральной рамки решения нашей задачи, с их расположением на сторонах большой квадратной рамки. Эти костяшки закрашены голубым цветом и, располагаясь в серединной части сторон большой квадратной рамки, делят ее на четыре фрагмента по 6 костяшек. Каждый из этих фрагментов начинается и заканчивается узловым числом, а сумма всех чисел в каждом фрагменте равна 36.
Таким образом, поиск решений исходной задачи с пятью рамками 4×4 сводится к поиску составленных из костяшек домино больших квадратных рамок 15×15, удовлетворяющих условиям:
- костяшки выложены по правилам домино;
- в серединной части каждой стороны расположены четыре костяшки, заданные четырьмя узловыми числами;
- сумма чисел на костяшках в четырех угловых фрагментах рамки (каждый такой уголок состоит из шести костяшек) равна 36;
- каждый такой фрагмент начинается и заканчивается соответствующим узловым числом.
Построив большую квадратную рамку, в которой выполнены все эти условия, ее можно трансформировать в фигуру, составленную из пяти равных квадратных рамок, повторив в обратном порядке процесс, описанный выше, и получить решение нашей основной задачи. Тем самым, кстати, мы установили взаимно однозначное соответствие между «доминошными» большими квадратными рамками 15×15 и фигурами из пяти рамок 4×4.
Исследованием квадратных рамок 15×15 занимался Яков Перельман. В своих книгах «доктор занимательных наук» формулирует интереснейшие задачи и раскрывает их секреты, умело демонстрируя применение математических приемов. Например, в книге «Живая математика» есть глава «Математика в играх», которая открывается серией задач и головоломок с домино. Одной из задач этой серии — как раз про квадратную рамку 15×15 (которую он также называет кольцом). При обсуждении задач Перельман попутно затрагивает и интересующие нас «доминошные» темы. Приведем выдержку из книги «Живая математика»:
«Читателя может заинтересовать вопрос: сколькими различными способами выполняется такая цепь или кольцо? Не входя в утомительные подробности расчета, скажем здесь, что число различных способов составления 28-косточковой цепи (или кольца) огромно: свыше 7 триллионов. Вот точное число: 7 959 229 931 520 (оно представляет собой произведение следующих множителей: 213·38·5·7·4231).»
Теперь мы знаем, что некоторые квадратные рамки из этого громадного числа подходят для построения решения нашей основной задачи.
Некоторые из квадратных рамок 15×15 обладают интересными свойствами. Рассмотрим одну из них, изображенную на рис. 7. Если ее разрезать между костяшками (6–3) и (3–3) и, начиная с костяшки (3–3), сворачивать получившеюся цепочку спирально, то, во-первых, получится прямоугольник 7×8, во-вторых, вдоль одной из его диагоналей удивительным образом выстраиваются пары от (0–0) до (6–6).

Рис. 7.
А вот квадратная рамка на рис. 8 хитрым образом складывается в фигуру, напоминающую кружевную салфетку, причем соприкасающиеся костяшки по-прежнему выложены по правилу домино. Убедитесь в этом, проследив, что последовательности костяшек и в квадратной рамке, и в «кружевной салфетке» действительно совпадают.

Рис. 8.
Квадратная рамка, приведенная на рис. 9 интересна тем, что если убрать из нее костяшку (0–0), то оставшаяся часть будет содержать 54 клетки, а это в точности совпадает с площадью поверхности куба 3×3×3. Заменив каждую костяшку этой квадратной рамки ее бумажным двойником, получим бумажный набор домино, выложенный в цепочку. Куб 3×3×3 можно оклеить этими бумажными «косточками» так, что на его поверхности образуется именно эта цепочка, оставшаяся после удаления костяшки (0–0), и она будет замкнутой, а сумма чисел на каждой грани куба постоянна и равна 28 (что составляет как раз шестую часть суммы чисел в полном наборе домино). На рис. 9 приведена развертка этого куба, красной линией показано как, «изворачиваясь» змейкой, приведенная цепочка плотно накрывает поверхность куба, замыкаясь при этом, то есть начало (2–0) и конец (0–5) цепочки совпадают. По развертке нетрудно убедиться, что сумма чисел на каждой грани куба действительно равна 28.

Рис. 9.
-
-
Среднюю рамку можно сложить из 8 костяшек, но тогда остальные рамки не сложаться, потому, что если один угол занят, то в рамке остается нечетное число костяшек! Не получится!
В статье в решении указано как строится центральная рамка! Удачи!-
-
Во-первых, речь должна идти о шести костяшках!
Во-вторых, каждая рамка состоит из 12 клеток. На первый взгляд, кажется, что центральную рамку можно сложить из шести костяшек. Но, если сложить центральную рамку из шести домино, то, например, на левую верхную рамку надо ещё 11 клеток, т.е. нечетное количество, а в каждой костяшке по две клетки, 11 на 2 не делится! Проблема! Значит, центральную рамку нельзя складывать из шести целых домино, а только так, как в решении задачи на рис. 3. А именно, центральная рамка складывается из четырех целых костяшек и четырех половинок.
-
-
-
Последние задачи















Рис. 1.