Карусель в квадрате

В обоих пунктах ответ — «можно». Придумайте последовательность поворотов, которая, например, меняет местами фишки с числами 2 и 6, так чтобы остальные фишки в итоге остались на своих местах. Можно ли аналогичным образом поменять местами любые две фишки?

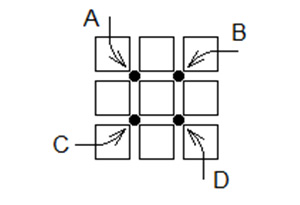
Рис. 2.

На рис. 2 буквами A, B, C и D обозначены центры возможных поворотов. Вокруг этих точек можно поворачивать четверки фишек (вокруг точки А, например, можно поворачивать фишки того квадратика 2×2, центром которого является эта точка). Повороты удобно обозначать степенями: A, A² и A³ — это повороты по часовой стрелке вокруг точки A на углы 90°, 180° и 270°, соответственно (направление поворотов — по часовой стрелке — выбрано для однозначности).

Построить квадрат, фишки которого пронумерованы «змейкой», можно, выполнив такую последовательность из семи поворотов: ABCB²C³AB². На рис. 3 по шагам показано, что при этом будет происходить с фишками.

Рис. 3.

Построить магический квадрат можно за шесть поворотов A³D³C²A²BA³ (рис. 4).

Рис. 4.

Задача решена, но может остаться чувство легкой неудовлетворенности, потому что непонятно, как найти решение и почему именно такие повороты приводят к нужному расположению фишек. Эти решения, кстати, — самые короткие, и найдены они были при помощи компьютерного поиска. Программу по просьбе автора написал чемпион России 2018 года по решению головоломок К. Т. Шамсутдинов.

Как же найти решения этих задач, используя только «карандаш и бумагу»? Давайте разберемся!

Будем называть квадраты 2×2 из фишек маленькими. Всего их в квадрате 3×3 помещается четыре штуки — по углам этого квадрата. Два маленьких квадратика могут пересекаться либо по одной фишке, либо по двум. Обе эти ситуации показаны на рис. 5.

Рис. 5.

Возможно ли в каждом из этих случаев, вращая маленькие квадратики вокруг их центров, поменять местами только две фишки, а остальные оставить на своих местах? Оказывается, оба этих случая хорошо изучены.

В журнале «Математика в школе» (№10 за 2009 год) была следующая задача (в немного другой формулировке). Головоломка «6» представляет собой прямоугольник 3×2 сложенный из квадратных фишек 1×1. Фишки пронумерованы в каждом ряду слева направо числами от 1 до 6. Фишки каждого квадрата 2×2 можно повернуть вокруг его центра на угол кратный 90°. Можно ли при помощи нескольких таких поворотов получить расположение, в котором только фишки 2 и 5 поменяются местами (рис. 6)? Легко увидеть, что это как раз левая конфигурация с рис. 5.

Рис. 6.

Авторы этой задачи (И. Акулич, К. Каибханов, С. Токарев) показали, что сделать это невозможно. Ее решению была посвящена отдельная статья в одном из следующих номеров журнала (хотя обычно решения предлагаемых задач довольно компактные). Статья непростого чтения, в ней все серьезно: пять страниц, шесть лемм, но результат интересен.

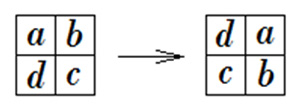
Рис. 7.

Оказывается, эта задача является частным случаем следующей общей задачи. В клетках прямоугольника m×n записаны числа 1, 2, 3, ..., mn, где 2 ≤ m ≤ n. Внутри прямоугольника разрешается выбрать любой квадрат 2×2 и переставить в нем числа по кругу (рис. 7). Для каких значений m и n числа в таблице можно упорядочить?

Исчерпывающий ответ на этот вопрос дал И. Акулич. Задача разрешима в том и только том случае, если m + n ≥ 6. Для таких прямоугольников он нашел многоходовые алгоритмы, позволяющие упорядочить числа таблицы. Для прямоугольника 2×3 задача оказалась неразрешимой. При исследовании этого случая использовался компьютер. Оказалось, что существующие 6! = 720 перестановок шести чисел можно разбить на шесть групп по 120 перестановок в каждой, причем, внутри каждой группы перестановки переводятся одна в другую при помощи поворотов маленьких квадратиков, а перестановки из разных групп одна в другую не переводятся. Перестановки (123456) и (153426) принадлежат разным группам, поэтому ответ на вопрос задачи — отрицательный. Именно это в своей статье показал К. Каибханов с помощью линейной комбинации двух инвариантов.

Еще один неожиданный вариант этой задачи. Оказывается, что она реализуется на кубике Рубика, если разрешить вращать только два слоя кубика: фронтальный и правый. На рис. 8 перемещаемые кубики — белые. Знатоки кубика Рубика, знают, что у него есть невозможные состояния: например, невозможно поменять местами только два угловых кубика (так, чтобы остальные в итоге остались на своих местах). А этому как раз соответствует задача про шесть квадратиков.

Рис. 8.

Теперь обратимся к правой части рис. 5. В журнале «Квант» (№6 за 2009 год) предлагалась такая задача. Из пронумерованных квадратных фишек 1×1 сложена фигура, содержащая два квадрата 2×2, причем фишка с номером 4 — общая (рис. 9, слева). Фишки каждого квадрата 2×2 можно повернуть вокруг его центра на угол, кратный 90°. Можно ли при помощи таких поворотов получить расположение, показанное на рис. 9 справа?

Рис. 9.

В отличие от первого случая, здесь фишки 1 и 2 можно поменять местами. Покажем, как это сделать. Заметим, что если не обращать внимания на перемещение остальных фишек, то фишки 1 и 2 нетрудно поменять местами. Для этого нужно выполнить всего четыре вращения квадратов 2×2 в такой последовательности: левый по часовой стрелке на 90°, правый против часовой стрелки на 90°, левый против часовой стрелки на 90°, и правый — на 180°. На рис. 10 показано перемещение фишек при этих вращениях.

Рис. 10.

Сравнивая начальное и конечное расположение фишек, проследим, какое перемещение совершила каждая фишка.

Рис. 11.

Если стрелками обозначить смещение каждой фишки, а точками отметить фишки, которые вновь оказались на своих местах, то получится схема с рис. 11. Фишки 1 и 2 поменялись местами, фишки 3 и 6 остались на своих местах, фишки 4, 5 и 7 переместились по циклу. Это значит, что если проделанную серию из четырех вращений повторить трижды, то фишки 4, 5 и 7 снова станут на свои места, а фишки 1 и 2 поменяются местами.

Вернемся к нашей задаче. На рис. 12 голубым цветом выделен фрагмент квадрата 3×3, который соответствует правой конфигурации с рис. 5. Используя повороты вокруг точек A и D, запишем найденную выше последовательность поворотов g = (AD³A³D²)³ для этого фрагмента. В результате выполнения последовательности g за 12 поворотов местами поменяются только фишки 2 и 6.

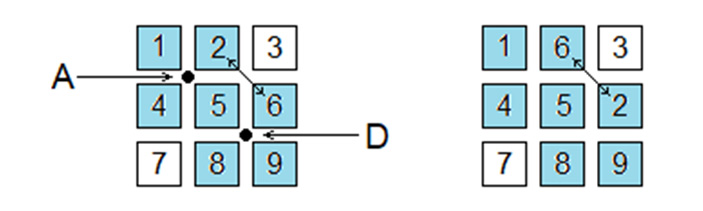
Рис. 12.

Чтобы построить квадрат, в котором фишки пронумерованы «змейкой», достаточно поменять местами фишки 4 и 6. Cначала необходимо выполнить подготовительный поворот А², переводящий фишку 4 на место фишки 2, затем применить серию поворотов g, которая поменяет местами фишки 4 и 6, после чего поворотом А² вернуть остальные фишки, (кроме 6) на свои места (рис. 13).

Рис. 13.

Чтобы построить магический квадрат, сначала тремя поворотами фишку 4 переводим в правый верхний угол, а фишку 6 переводим в левый нижний угол, например, так: A²BC². Выполним еще поворот A², переводящий фишку 5 в центр квадрата.

Рис. 14.

То, что получилось, показано на рис. 14 справа: белые фишки уже на своих местах, а в той части, которая выделена голубым, надо еще навести порядок. Но оказывается, что, используя последовательность поворотов g и вспомогательные повороты, в этой части можно менять местами любые две фишки. Покажем, например, как поменять местами фишки a и b (рис. 15). Для этого сначала переведем фишку a в середину верхней стороны квадрата, фишку b — в середину правой стороны квадрата. Получили расстановку, к которой можно применить последовательность поворотов g и поменять местами фишки a и b, после обратными подкрутками C³ и A³ (именно в таком порядке) возвращаем остальные фишки в исходное состояние.

Рис. 15.