Памяти Стивена Вайнберга

23 июля в техасском городе Остин скончался один из выдающихся ученых XX века, физик-теоретик Стивен Вайнберг. Вайнберг серьезно занимался разными областями науки, но, пожалуй, наиболее значимый вклад он оставил в физике элементарных частиц и космологии. За свою долгую научную карьеру он стал лауреатом множества престижнейших премий, включая и Нобелевскую премию по физике (полученную в 1979 году совместно с Шелдоном Глэшоу и Абдусом Саламом за создание единой теории электрослабых взаимодействий). Вайнберг вкладывал много сил и в популяризацию науки, некоторые его книги переведены на русский язык. Алексей Левин подводит итог жизненного и научного пути великого ученого, отдавая дань его достижениям.
Вехи великой жизни
23 июля научный мир понес тяжелую утрату. В столице штата Техас Остине на 89-м году жизни скончался великий физик-теоретик, лауреат Нобелевской и множества других премий, член Национальной Академии наук США и Лондонского Королевского общества Стивен Вайнберг. На момент написания этой статьи причина его смерти еще не была обнародована.
Вайнберг вошел в историю науки прежде всего как один из создателей новой теории элементарных частиц, позволившей объединить в единой математической конструкции квантовую электродинамику и теорию слабых взаимодействий, которая описывает взаимные превращения кварков и лептонов, в том числе и нейтрино. Эта модель, известная как теория электрослабых взаимодействий, была создана в 60-е годы прошлого века Вайнбергом, Шелдоном Ли Глэшоу и умершим четверть века назад пакистанским физиком Абдусом Саламом. В 1979 году эти ученые получили за нее Нобелевскую премию. В следующем десятилетии ее удалось интегрировать с теорией межкварковых взаимодействий — квантовой хромодинамикой. Эта исследовательская программа, в которой принимал участие и Вайнберг, привела к созданию Стандартной модели элементарных частиц, которая, по общему признанию, стала самой грандиозной и наиболее успешной теорией фундаментальной физики за все время ее существования.
Но Вайнберг занимался отнюдь не только физикой микромира. В 1970-е годы он стал одним из лидеров международной группы ученых, занимавшихся объединением теории элементарных частиц с космологией, наукой, которая до этого развивалась практически автономно. Эти исследования, в которых огромную роль сыграли и советские физики, уже в 1980-е годы повлекли за собой создание инфляционной космологии. Она стала неотъемлемой частью современной теории рождения и эволюции Вселенной, которую называют Стандартной космологической моделью.
Стивен Вайнберг опубликовал более трех сотен статей, как чисто научных, так и популярных, и, в общей сложности, 17 книг. В 1972 году он выпустил монографию Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity, которая превратилась в настольную книгу целого поколения космологов и астрофизиков. Пятью годами позже появилась небольшая книга The First Three Minutes: A Modern View of the Origin of the Universe — очень элегантное общедоступное изложение ранней истории мироздания. В 1999 году он завершил работу над тремя томами фундаментального курса квантовой теории поля, которые выходили из печати в 1995, 1996 и 2000 годах. В 2008 году Вайнберг порадовал читателей великолепной книгой по общей космологии. Все эти монографии доступны в русском переводе, ссылки можно найти в посвященной Вайнбергу статье в русской «Википедии».
Вайнберг продолжал более чем активно работать и во втором десятилетии нашего века. Уже после 2010 года он опубликовал блестящие и оригинальные Lectures on Quantum Mechanics (первое издание в 2012 году, второе — в 2015). За этим учебником в 2019 году последовали Lectures on Astrophysics (к сожалению, книга, на мой взгляд, получилась не совсем удачной — она перегружена математикой и содержит недостаточно фактических данных) и появившаяся недавно последняя большая работа Foundations of Modern Physics (2021). В 2015 году издательство HarperCollins опубликовало его труд по истории астрономии и физики To Explain the World: The Discovery of Modern Science, где эволюция этих наук прослежена от древней Греции до ньютоновской революции (эту книгу уже через год подарило нашим читателям московское издательство «Альпина нон-фикшн»). Сразу после ее выхода в свет в 2015 году Вайнберг оказал мне честь беседой об этой монографии, которая без задержки появилась на «Элементах» (см. История науки от Стивена Вайнберга, «Элементы», 21.04.2015). Хочу отметить абсолютно антипостмодернистский характер этого труда, в котором эволюция естественных наук представлена как сознательный и целенаправленной поиск объективного и доказуемого знания о Природе. За это на автора ополчились некоторые историки и социологи науки. Могу привести в пример хотя бы откровенно несправедливую статью Стивена Шейпина в The Wall Street Journal (!), которую Вайнберг разбил в пух и прах своим коротким, но блестящим ответом.
И это еще не полный список его книг, не говоря уже о сотнях статей, лекций и интервью (кстати, его последнее эссе на одну из ключевых тем фундаментальной физики было опубликовано уже в этом году). Перечень его публикаций и должностей с начала научной карьеры до 2015 года можно найти здесь. В общем, активность и работоспособность Стивена Вайнберга в молодости, в зрелом возрасте и в глубокой старости вполне конгениальны его научному гению.
Внешняя сторона биографии Вайнберга, в отличие от его трудов, ничем особенным не выделяется. Он родился 3 мая 1933 года в семье евреев-эмигрантов, поселившихся в Нью-Йорке. Отец Стивена Фредерик работал судебным стенографом, мать Ева вела домашнее хозяйство. Мальчик читал научно-популярные книги отца-основателя космологической модели горячей Вселенной Георгия Гамова, однако если и интересовался наукой, то химией, а не астрофизикой или космологией. Любовь к химии привела его в мужскую школу с углубленным изучением физики и математики, основанную в Бронксе в 1938 году решением нью-йоркского городского Совета по образованию. В этой «физматшколе», расположенной в построенном в 1918 году здании на пересечении Крестон-авеню и 184-й улицы, он познакомился и подружился с еврейским мальчиком из семьи выходцев из России, своим будущим коллегой и партнером Шелли Глэшоу.

Научная школа в Бронксе (Bronx High School of Science). Слева — вход в старое здание, располагавшееся на пересечении Крестон-авеню и 184-й улицы. Оно служило школе с момента ее основания в 1938 году до 1959 года. Затем школа переехала в специально построенное для нее здание на 205-й улице (справа). Фото с сайта en.wikipedia.org
Эксперимент нью-йоркского «гороно» оказался более чем успешным. Научная школа в Бронксе (Bronx High School of Science) дала миру восемь нобелиатов (семеро по физике, один по химии), столько же лауреатов Пулитцеровской премии, шесть обладателей Национальной медали науки (разумеется, и Вайнберга, который был награжден ею в 1991 году), 29 членов Национальной Академии наук США и 22 члена Национальной Академии инженерных наук, да еще и (вишенка на торте!) двух конгрессменов. Стоит отметить, что в нобелевской «команде» выпускников БНШ также состоят один из создателей квантовой теории сверхпроводимости Леон Купер, корифей квантовой хромодинамики Хью Дэвид Политцер и крупный специалист по физике нейтрино Мелвин Шварц. А если говорить о столь же ярких звездах на небосводе физики, не съездивших в Стокгольм, нельзя не упомянуть хотя бы прославившегося исследованием векторных мезонов Дзюна Джона Сакураи (Jun John Sakurai) и одного из отцов-основателей теории струн Леонарда Сасскинда. В общем, не слабо. Во всяком случае, мне не не известно ни единого среднего учебного заведения со столь блестящим послужным списком. Может быть, эта информация покажет адептам домашнего образования, что способна дать хорошая школа. Кстати, перечисленные ученые получили аттестаты не в 8 лет, как Алиса Теплякова, а в 17–18, и ни один из них не считался вундеркиндом.
Вайнберг и Глэшоу получили аттестаты в 1950 году. Оба поступили в Корнеллский университет и покинули его спустя 4 года с дипломами бакалавров искусств. Из Корнелла они ушли в два самых элитных университета США: Вайнберг — в Принстон, а его друг — в Гарвард. Оба защитили докторские диссертации по физике: Вайнберг — в 1957 году, Глэшоу — годом позже. Несколько лет они проработали в Калифорнийском университете в Беркли, а в 1966 году перебрались в Кембридж — не тот, что в Англии, а тот, что в штате Массачусетс. Глэшоу получил профессуру в Гарварде, а Вайнберг там же обрел должность лектора и позицию гостевого профессора Массачусетского Технологического института. В 1969 году он стал полным профессором МТИ, но четырьмя годами позже после ухода из Гарварда одного из создателей квантовой электродинамики Джулиана Швингера получил его кафедру, а также должность старшего научного сотрудника (Senior Scientist) Смитсоновской астрофизической обсерватории.
Скорее всего, Вайнберг остался бы в Гарварде, если б не личные обстоятельства. В 1954 году он женился на своей сокурснице по Корнеллу Луизе Голдвассер; в 1963 году у супругов родилась единственная дочь Элизабет, которая избрала профессию врача. Луиза Вайнберг (Louise Weinberg) стала крупным юристом, специалистом по федеральной судебной системе и конституционному праву. В 1980 году она получила должность профессора права в кампусе Техасского университета в Остине. Вайнберг провел еще два года в Кембридже, после чего перебрался в Остин на факультет физики и астрономии. Там он создал мощную команду физиков-теоретиков мирового уровня. До конца жизни Вайнберг не выходил в отставку и, как когда-то говорили, умер на своем посту. 24 июля его смерть была подтверждена в новостном бюллетене Техасского университета.
Стивен Вайнберг был человеком многих талантов и интересов. Он был блестящим популяризатором науки, чьи труды не утратили значения и поныне. Он любил и знал поэзию и театр, очень нетривиально интересовался философией и историей науки. В общем, был человеком на все времена.
Интересно, что миграция в космологию в определенном смысле сыграла с Вайнбергом злую шутку. В конце 1960-х годов он неоднократно пытался доказать, что из вычислений на основе модели электрослабых взаимодействий можно исключить бесконечности, как это в свое время удалось сделать с квантовой электродинамикой. Однако эти иследования он вел урывками и, вероятно, не в полную силу. В результате это свойство модели, так называемую ренормализуемость, доказал не он, а другие физики, о чем у нас пойдет речь дальше. Вайнберг впоследствии очень сожалел об этой небрежности, в чем признался в одном из интервью — правда, данном не мне (см. A. Lightman, R. Brawer, 1990. Origins: The Lives and Worlds of Modern Cosmologists).
Вайнберг был убежденным атеистом и считал религию «оскорблением человеческого достоинства». Вот еще одна его очень известная мысль: «Наука не делает невозможной веру в Бога, однако она позволяет не верить в Бога». Он был уверен, что главная ценность науки состоит в обретении истины, и настаивал, что «на самом фундаментальном уровне наукой занимаются отнюдь не для какой бы то ни было практической цели». И мое любимое изречение: «Попытка понять Вселенную — это одна из очень немногих вещей, которые хоть немного поднимают человеческую жизнь над уровнем фарса и наделяют ее благодатью трагедии». Тут уж, воистину, ни убавить, ни прибавить. Все эти цитаты можно найти на этом сайте.
И последнее. Несмотря на атеизм, Вайнберг полностью принимал идеологию и практику сионизма и всегда защищал Израиль от нападок. В 2006 и 2007 годах он дважды отменял запланированные визиты в Британию в знак протеста против усиления антиизраильских и антисемитских настроений в английском общественном мнении. В этом он был так же тверд, как в своих научных убеждениях.
С моей стороны было бы слишком самонадеянно подробно описывать все научные исследования Вайнберга, да и места для этого недостаточно. Поэтому я расскажу об его главном вкладе в теоретическую физику, который был увенчан Нобелевской премией. Начать придется издалека — аж с конца позапрошлого века.
От электрона к кваркам
Экспериментальное и теоретическое иссследование элементарных частиц насчитывает примерно 125 лет. В 1897 году британский физик Джозеф Джон Томсон в ходе экспериментов по прохождению тока через разреженные газы открыл электрон, за что через девять лет был удостоен Нобелевской премии. Через двадцать лет Эрнест Резерфорд доказал, что ядра водорода входят в состав ядер всех прочих элементов, и позднее назвал их протонами. В тридцатые годы ХХ века были обнаружены нейтрон, мюон и позитрон и предсказано существование нейтрино. Тогда же первый (на тот момент — еще будущий) японский лауреат Нобелевской премии по физике Хидэки Юкава построил теорию ядерных сил, переносимых гипотетическими частицами в сотни раз тяжелее электрона, но много легче протона (теперь они зовутся мезонами).
В 1947 году следы мезонных распадов впервые нашли на фотопластинках, экспонированных в космических лучах. Открытые в ходе этих экспериментов частицы называются пи-мезонами, или просто пионами. Позже обнаружили и другие мезоны, причем некоторые из них тяжелее не только протона, но и ядра гелия. Физики также открыли множество различных барионов, массивных, а посему очень короткоживущих родичей протона и нейтрона. Стоит напомнить, что любой мезон состоит из кварка и антикварка, а барионы сложены из кварковых троек.
Когда-то все эти частицы называли элементарными, но такая терминология давно устарела. Элементарными принято считать частицы, которые, по современным представлениям, ни из чего не состоят и представляют собой точечные объекты. Одни из них имеют полуцелый спин и принадлежат классу фермионов, другие — целочисленный, это бозоны. Фермионная группа состоит из лептонов и кварков. Заряженные лептоны — это электрон и его массивные аналоги мюон и тау-частица (и, естественно, их античастицы). У каждого лептона имеется нейтральный партнер в лице одной из трех разновидностей нейтрино (тоже с античастицами). Бозонное семейство представлено частицами со спином, равным единице, которые переносят взаимодействия между кварками и лептонами. Некоторые из них не имеют ни массы, ни электрического заряда — это глюоны, обеспечивающие межкварковые связи в мезонах и барионах, и фотоны, кванты электромагнитного поля. Слабые взаимодействия, которые проявляют себя в процессах бета-распада, обеспечиваются тройкой массивных частиц — двумя заряженными и одной нейтральной.
Но это не всё. Почти полвека назад была предсказана еще одна элементарная частица, которой присвоили имя живого человека, шотландского физика Питера Хиггса. Подобно переносчикам фундаментальных взаимодействий, она имеет целочисленный спин и принадлежит классу бозонов (отсюда и название — бозон Хиггса). Однако ее спин равен не единице, а нулю, и в этом отношении у нее нет аналогов в микромире. Ее пытались найти десятки лет и в конце концов в 2012 году обнаружили в серии экспериментов на Большом адронном коллайдере в ЦЕРН (см. новость Хиггсовский бозон: открытие и планы на будущее, «Элементы», 16.07.2012). Если бы его не удалось обнаружить, ключевые положения Стандартной модели элементарных частиц пришлось бы признать несостоятельными.
Могущество калибровочных симметрий
Теперь перейдем к созданию теории электрослабых взаимодействий. Начало пути к ее созданию можно отсчитывать от короткой статьи Conservation of Isotopic Spin and Isotopic Gauge Invariance, опубликованной 1954 году в журнале Physical Review. Ее авторами были перебравшийся в США китайский физико-теоретик Янг Чжэньнин и его коллега по Брукхэйвенской национальной лаборатории Роберт Миллс. В те годы экспериментаторы с удивительным постоянством открывали все новые и новые частицы, изобилие которых никак не удавалось объяснить. В поисках перспективных идей Янг и Миллс решили опробовать возможности очень интересной симметрии, которой подчиняется квантовая электродинамика. К тому времени эта теория доказала свою способность давать великолепно согласующиеся с опытом результаты. Правда, в ходе некоторых вычислений там появляются бесконечности, однако от них можно избавляться с помощью математической процедуры, названной перенормировкой.
Симметрию, заинтересовавшую Янга и Миллса, в 1918 году ввел в физику великий немецкий математик Герман Вейль. Он назвал ее калибровочной, и это название сохранилось до наших дней. В квантовой электродинамике калибровочная симметрия проявляется в том, что волновую функцию свободного электрона, которая представляет собой вектор с вещественной и мнимой частью, можно непрерывно поворачивать в каждой точке пространства-времени, причем на произвольные углы, никак не связанные друг с другом. Такая симметрия называется локальной — в отличие от глобальной симметрии, когда угол поворота не зависит от координат (иначе говоря, он один и тот же по всему объему пространства-времени). Эта операция (на формальном языке, произвольное изменение фазы волновой функции) приводит к тому, что в уравнении движения электрона появляются добавки, которые необходимо скомпенсировать, чтобы оно выглядело так же, как и до преобразования (уравнение, которое удовлетворяет такому требованию, называется ковариантным относительно той или иной группы преобразований). Для этого туда вводится дополнительный член, который физически можно интерпретировать как электромагнитное поле, взаимодействующее с электроном. Квантом этого поля, как известно, является фотон, безмассовая частица с единичным спином. Таким образом, из локальной калибровочной симметрии уравнения свободного электрона следует существование фотонов (а также, в качестве дополнительного бонуса, постоянство электрического заряда). Можно сказать, что эта симметрия автоматически предписывает электрону взаимодействовать с электромагнитным полем. Любой фазовый сдвиг становится актом такого взаимодействия — например, испусканием или поглощением фотона.
Связь квантовомеханической калибровочной симметрии с электромагнетизмом была выявлена еще в 1920-е годы, однако особого интереса не вызывала. Точности ради стоит отметить, что аналогичной симметрии подчиняются и классические максвелловские уравнения электромагнитного поля, причем в этом случае она тоже гарантирует сохранение электрического заряда. Янг и Миллс первыми попытались применить калибровочную симметрию для конструирования уравнений, описывающих частицы иной природы, нежели электрон и, соответственно, иные поля, нежели электромагнитное. Эта вроде бы чисто формальная инновация стала началом конструирования нового типа теорий, которые полностью преобразовали наше понимание квантовых полей и элементарных частиц.
А началость всё с малого. Янг и Миллс занялись двумя «старейшими» барионами, протоном и нейтроном. Хоть эти частицы далеко не тождественны (у них разные массы, протон заряжен, а нейтрон нет), но по отношению к ядерным силам (но, конечно, не электромагнитным!) они ведут себя практически одинаково и имеют почти одинаковую массу. В 1932 году Вернер Гейзенберг показал, что протон и нейтрон можно формально считать различными состояниями одной и той же частицы. Для их описания он ввел новое квантовое число, изотопический спин. Согласно его схеме, абсолюное значение изотопического спина одно и то же, однако проекции изоспина в специально выбранном для него абстратном пространстве различны (согласно стандартной конвенции, протону соответствует значение проекции изтопического спина, равное +1/2, а нейтрону −1/2). Алгебра операций с изотопическим спином совпадает с соответствующей алгеброй для обычного спина электронов и прочих фермионов. Поскольку сильное взаимодействие не делает различий между протонами и нейтронами, оно сохраняет их полный изотопический спин — подобно тому, как электромагнитное взаимодействие сохраняет электрический заряд.
Янг и Миллс решили найти локальные калибровочные преобразования, сохраняющие изоспиновую симметрию. Было ясно, что они не могут совпадать с калибровочными преобразованиями квантовой электродинамики — хотя бы потому, что речь шла не об одной, а о двух частицах. Янг и Миллс доказали, что такие преобразования генерируются теми же матрицами Паули, которые применяют для работы с электронами и прочими частицами со спином, равным 1/2. Это было естественно, поскольку, как я только что отметил, изотопический спин по своим алгебраическим свойствам аналогичен обычному. Требование локальной калибровочной симметрии в этом случае приводит к рождению полей, чьи кванты переносят взаимодействия между протонами и нейтронами. Квантов (как и полей) в данном случае было три: два заряженных (положительно и отрицательно) и один нейтральный. Они имели единичный спин (такие частицы называются векторными бозонами) и нулевую массу. Как и положено безмассовым частицам, они были обязаны двигаться в пространстве со скоростью света.
Теория B-полей, как их окрестили соавторы, была очень красивой, но не выдерживала испытания опытом. Нейтральный B-бозон еще можно было попробовать отождествить с фотоном, но его заряженные собратья явно оставались не при деле. Согласно квантовой механике, посредниками в переносе короткодействующих сил могут быть лишь достаточно массивные виртуальные частицы. Радиус действия ядерных сил не превышает 10−13 см, и безмассовые бозоны Янга и Миллса явно не могли претендовать на роль их переносчиков. Опять же, физики никогда не регистрировали таких частиц, хотя в принципе заряженные безмассовые бозоны легко обнаружить в эксперименте. Янг и Миллс доказали, что локальные калибровочные симметрии «на бумаге» могут порождать силовые поля неэлектромагнитной природы, однако физическая реальность этих полей была чистой гипотезой.
В поисках электрослабого двуединства
Следующий шаг к электрослабой симметрии был сделан в 1957 году. К тому времени два американо-китайских физика-теоретика (тот же Янг и его соавтор Ли Чжэндао) предположили, а экспериментаторы доказали, что при бета-распадах не сохраняется четность (иначе говоря, нарушается зеркальная симметрия). Этот неожиданный результат заинтересовал многих физиков, среди которых был и Джулиан Швингер. Он выдвинул гипотезу, что слабые взаимодействия между лептонами (до кварков наука еще не дошла!) переносятся тремя векторными бозонами — фотоном и парой заряженных частиц, аналогичных B-бозонам. Отсюда следовало, что эти взаимодействия состоят в партнерстве с электромагнитными силами. Швингер этой проблемой больше не занимался, однако предложил ее Шелдону Глэшоу, который тогда еще был его аспирантом.

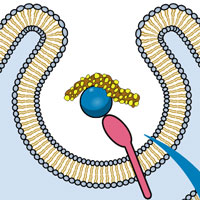
Фейнмановские диаграммы, изображающие примеры электромагнитного (а) и слабых (б, в) взаимодействий. Рисунок из статьи В. Рубаков, 2012. К открытию бозона Хиггса
Работа растянулась на четыре года. После ряда неудачных попыток Глэшоу построил модель слабого и электромагнитного взаимодействий, основанную на объединении калибровочных симметрий электромагнитного поля и полей Янга и Миллса. Помимо фотона, в ней фигурировали еще три (а не два, как у Швингера!) новых векторных бозона — пара заряженных W+ и W− и один нейтральный Z. Глэшоу также первым осознал, что предложенная им конструкция откроет путь к устранению бесконечностей из теории превращений элементарных частиц, обусловденных слабыми взаимодействиями (иначе говоря, он увидел путь к созданию ренормализуемой теории слабых взаимодействий).
Однако у модели Глэшоу была явная слабость, которая тогда казалась неустранимой. Все три «новых» бозона имели нулевую массу, что создавало очень неприятную проблему. У слабого взаимодействия радиус на два порядка меньше, нежели у сильного, поэтому ему тем более требуются очень массивные посредники. К тому же наличие нейтрального переносчика требовало допустить возможность бета-переходов, не меняющих электрический заряд, а таковые тогда не были известны. В то же время такой переносчик был необходим, поскольку без него не удавалось обеспечить несохранение четности в слабых взаимодействиях, которое тогда уже было надежно доказано в эксперименте. Из-за всего этого после публикации своей модели в конце 1961 года Глэшоу потерял интерес к объединению слабого и электромагнитного взаимодействий и надолго ушел в физику кварков.
Гипотеза Швингера заинтересовала и Абдуса Салама, который вместе с англичанином Джоном Клайвом Уордом построил модель, похожую на модель Глэшоу. Он тоже столкнулся с безмассовостью калибровочных бозонов и даже придумал способ ее устранения. Салам знал, что их массы нельзя ввести «от руки», поскольку при этом разрушалась калибровочная симметрия и теория явно становилась ненормируемой. Однако он рассчитывал обойти это затруднение с помощью спонтанного нарушения симметрии, которое было давно известно в других областях физики. Вот хрестоматийный пример. Основное уравнение теории ферромагнетизма обладает симметрией относительно любых поворотов. Однако у реального ферромагнетика имеется ось намагниченности, которая создает в пространстве выделенное направление. Поле такого ферромагнетика симметрично только относительно поворотов вокруг этой оси. Так что базисная теория полностью симметрична, а объект ее описания — нет. Вот и Салам хотел найти решения уравнений движения бозонов, которые не обладают калибровочной симметрией, присущей сами исходным уравнениям. Этой задачей он заинтересовал Стивена Вайнберга.
Но не тут-то было. В 1961 году английский физик Джеффри Голдстоун сделал очень интересное открытие. Он занимался анализом непрерывных симметрий, масштаб которых зависит от значений тех или иных числовых параметров (существуют также дискретные симметрии — например, уже упоминавшееся зеркальное отражение или обращение времени). Годстоун на ряде примеров показал, что в релятивистских квантовых теориях поля спонтанное нарушение глобальной симметрии рождает безмассовые частицы с целочисленным спином. Три года спустя это утверждение строго доказал профессор Чикагского университета Йоитиро Намбу. Салам с Вайнбергом попытались его опровергнуть, но только усилили его обоснование. В физической литературе оно фигурирует как теорема Голдстоуна — Намбу, а предсказанные ею частицы получили название голдстоуновских бозонов. Загадка выглядела неразрешимой, и они, как в свое время Глэшоу, занялись другими вещами.
Бозон Хиггса и его родители
Помощь неожиданно пришла от специалистов по физике конденсированных сред. В 1961 году Намбу отметил, что при переходе нормального металла в сверхпроводящее состояние прежняя симметрия электронов проводимости спонтанно нарушается из-за рождения электронных пар, но при этом не появляется никаких безмассовых частиц. Очень важно, что здесь имеет место не глобальное, а локальное нарушение симметрии. Спустя два года сотрудник теоретического отдела фирмы «Белл» Филип Уоррен Андерсон на том же примере продемонстрировал, что того же можно ожидать и от других калибровочных полей с нарушенной локальной симметрией. Он даже предсказал, что голдстоуновские бозоны и векторные бозоны полей Янга — Миллса могут как-то ликвидировать друг друга, оставляя после себя массивные частицы.
Этот прогноз оказался пророческим. В 1964 году его оправдали физики из брюссельского Свободного университета бельгиец Франсуа Энглер и американец Роберт Браут, уже упоминавшийся Питер Хиггс и сотрудники лондонского Импириэл-колледжа Джеральд Гуральник (Gerald Guralnik) и Томас Киббл, работавшие вместе с гостем из США Карлом Ричардом Хагеном (Carl Hagen). Они независимо и разными способами показали, что в полях Янга — Миллса не соблюдаются условия применимости теоремы Голдстоуна, поскольку эти поля обладают не глобальной, а локальной симметрией. Они также нашли способ снабдить возбуждения этих полей ненулевой массой — сейчас его называют механизмом Хиггса. При этом Хиггс первым в явной форме отметил, что из его модели вытекает существование массивного скалярного бозона, а два года спустя даже проанализировал возможный распад этой гипотетической частицы на два тяжелых векторных бозона, который и был открыт девять лет назад. Так что общепринятый ныне термин «бозон Хиггса» вполне заслужен. Стоит отметить, что в 1965 году к сходным выводам пришли московские физики Александр Поляков и Александр Мигдал, однако их статья была опубликована только в 1966 году (A. A. Migdal, A. M. Polyakov, 1966. Спонтанное нарушение симметрии сильного взаимодействия и отсутствие безмассовых частиц).
На сцену выходит Вайнберг
Специалисты по физике элементарных частиц заметили и оценили работы этой группы отнюдь не сразу. Лишь в конце 1967 года Вайнберг в короткой статье A Model of Leptons предложил единую модель электрослабого взаимодействия, в которой тройка векторных бозонов получает массу на основе механизма Хиггса. Годом позже то же самое сделал и Салам. Вайнберг даже построил конкретную модель, в рамках которой детально описал взаимодействие калибровочных полей. Правда, она относилась только к лептонам и вообще содержала ряд упрощений, но как иллюстрация работала очень убедительно. В частности, Вайнберг довольно точно вычислил массу заряженных векторных бозонов (по его оценке, порядка 60 ГэВ), а также показал, что их нейтральный партнер должен быть несколько тяжелее.
Однако потом процесс конструирования калибровочной теории электрослабых взаимодействий почти остановился. В то время экспериментаторам не было известно ни одного процесса с участием гипотетического нейтрального векторного бозона (такого, как, скажем, рассеяние мюонного нейтрино на электроне). Кроме того, ни Вайнберг, ни Салам не смогли доказать ренормализуемость своих моделей. В итоге они сами потеряли к ним интерес и к началу 1970-х годов это направление исследований казалось зашедшим в тупик. Не случайно в 1967–70 годах на работу Вайнберга не появилось ни единой ссылки, и только одна за весь 1971 год. Сейчас точное число ссылок на эту работу даже трудно подсчитать, но, во всяком случае, оно превышает 15 тысяч.
Однако вскоре все изменилось. В 1971 году молодой голландский физик Герард 'т Хоофт показал, что калибровочная теория электрослабых взаимодействий в формулировке Вайнберга и Салама скорее всего поддается перенормировке и, следовательно, имеет четкий физический смысл. Вскоре он же вместе со своим (скончавшимся в начале января этого года) научным руководителем Мартинусом Велтманом дали строгое доказательство ренормализуемости; то же самое независимо сделали безвременно погибший в автокатастрофе американский физик-теоретик корейского происхождения Бенджамин Ли (Benjamin W. Lee) и француз Жан Зинн-Жустен (Jean Zinn-Justin). Теория прочно встала на ноги после 1973 года, когда на церновской пузырьковой камере Гаргамель (Gargamelle) экспериментаторы зарегистрировали так называемые слабые нейтральные токи, указывающие на существование незаряженного промежуточного бозона. Прямая регистрация всех трех векторных бозонов по их продуктам распада была осуществлена под руководством Карло Руббиа и Симона ван дер Мера в ЦЕРН лишь в 1982–83 годах на специально построенном для этой цели протон-антипротонном коллайдере. Как я уже отметил, Глэшоу, Вайнберг и Салам получили за свои работы Нобелевскую премию в 1979 году, Велтман и 'т Хоофт — в 1999 году. Теория электрослабых взаимодействий (а вместе с нею и бозон Хиггса) уже давно стала неотъемлемой частью Стандартной Модели элементарных частиц.

Лауреаты Нобелевской премии по физике 1979 года. Слева направо: Шелдон Ли Глэшоу, Абдус Салам, Стивен Вайнберг. В краткой формулировке Нобелевского комитета отмечено, что премия вручена «за вклад в объединенную теорию слабых и электромагнитных взаимодействий между элементарными частицами, в том числе предсказание слабых нейтральных токов». Фото с сайта nobelprize.org
Рождение массы
Для рассказа о работах Вайнберга в общем-то не обязательно объяснять действие механизма Хиггса. Но все же я попытаюсь это сделать.
Как уже говорилось, в его основе лежат скалярные поля с бесспиновыми квантами — поля Хиггса. Как считается, в нашей Вселенной они возникли спустя 10 пикосекунд после Большого Взрыва и теперь заполняют всё пространство. Важнейшим свойством хиггсовских полей является то, что у них минимум плотности энергии достигается при ненулевых значениях их величины (для сравнения — плотность энергии электрического поля пропорциональна квадрату его напряженности и, следовательно, зануляется при ее нулевом значении). Это и есть устойчивое состояние хиггсовских полей, их истинный вакуум (вакуум с неминимальной плотностью энергии называется ложным). Это свойство выглядит парадоксально, но оно вполне реально. С точки зрения физики, спонтанное нарушение симметрии — это как раз «миграция» системы из ложного вакуума к истинному.
Нередко пишут, что элементарные частицы обретают массу в результате торможения хиггсовским полем, но это чересчур механистическая аналогия. В теории электрослабого взаимодействия фигурируют четыре хиггсовских поля (каждое со своими квантами) и четыре векторных бозона, порожденных калибровочными симметриями — два нейтральных и два заряженных. Сами по себе они не имеют массы — иначе говоря, в уравнения, которые описывают их динамику, массовый член не входит. Механизм Хиггса как раз и исправляет это нежелательное обстоятельство. Три калибровочные бозона (их обозначают символами W+, W− и Z0), два заряженных и один нейтральный, поглощают по одному кванту трех хиггсовских полей. В результате они обретают массу и, как следствие, способность переносить короткодействующие силы. Последний калибровочный бозон ничего не поглощает и остается безмассовым — это, конечно, фотон. Съеденные хиггсовские кванты ненаблюдаемы (физики их называют духами), в то время как их выживший четвертый собрат сам обладает массой и должен наблюдаться при энергиях, достаточно высоких для его рождения (сейчас известно, что это примерно 125 ГэВ). В общем, это именно те процессы, которые ухитрился предсказать Андерсон.
Механизм Хиггса можно описать и по-другому. Поскольку все четыре векторных калибровочных бозона изначально безмассовы и потому обладают световой скоростью, их волновые функции колеблются только в плоскости, перпендикулярной направлению движения (этим же свойством, как известно, обладает и фотон). После поглощения хиггсовских квантов бозоны W+, W− и Z0 обретают дополнительные волновые компоненты, осциллирующие вдоль направления скорости. Эти продольные волны придают частицам инерционность и, следовательно, наделяют массой. По данным коллаборации CDF, масса W-бозонов равна 80,385 ГэВ; более массивный Z0 тянет на 91,188 ГэВ.
Изначально механизм Хиггса применяли только для интерпретации возникновения массы у векторных бозонов теории электрослабых взаимодействий. Позднее с его помощью удалось объяснить массы кварков и заряженных лептонов (глюоны массы не имеют, но механизм Хиггса их и не затрагивает). Он оказался полезным и для понимания массы нейтрино (хотя для нее есть и другое объяснение), и для объяснения смешивания кварков различных семейств. Хиггсовские частицы появляются и в рамках различных обобщений Стандартной модели, причем в немалых количествах. В общем, их нынешняя популярность вполне заслужена.
Под занавес стоит добавить уточнение технического характера. Калибровочные симметрии теории электрослабого взаимодействия описывается произведением двух довольно простых непрерывных групп, они же группы Ли. Генераторами одной группы служат матрицы Паули, а другая в этом качестве обходится мнимой единицей. Для любителей математики: эти группы связаны с группами SU(2) и U(1), однако обладают своей спецификой. Первой симметрии соответствуют три калибровочных бозона, два заряженных и один нейтральный. Вторая группа тоже порождает еще один бозон без электрического заряда, B0.
Заряженные бозоны (получившие массу на основе механизма Хиггса) сами по себе являются физически наблюдаемыми частицами. Ситуация с двумя нейтральными бозонами несколько сложнее. Они образуют два смешанных состояния, которые уже можно обнаружить в эксперименте. Одно из них — это фотон, второе — самый массивный векторный бозон Z0. Степень смешивания «родительских» состояний определяется особым параметром, так называемым углом Вайнберга. Его численная величина не вытекает из теории, а определяется из эксперимента. Она не является константой, поскольку зависит от масштаба энергий изучаемых процессов (или, что эквивалентно, от величины импульса, который передается между частицами в ходе реакций, на основе которых измеряется этот угол). В экспериментах по рождению Z0 при столкновениях электронов и позитронов измеренный квадрат синуса угла Вайнберга оказался равен 0,2312, что соответствует углу 28,7 градуса.
Я упоминал свою беседу со Стивеном Вайнбергом, которую можно найти на «Элементах». Однако первое интервью он мне дал тремя годами раньше, в конце 2012 года. Это случилось вскоре после первого, тогда еще пробного детектирования бозона Хиггса. Интервью было опубликовано в журнале «Популярная механика» (в номере за январь 2013 года). Думаю, что сейчас самое время к нему вернуться. Живая речь великого физика заслуживает многократного прочтения.
— Профессор Вайнберг, позвольте начать с вопроса о приоритетах. Как Вы считаете, кому принадлежит главная заслуга в разработке калибровочных теорий?
С. В.: Строго говоря, калибровочный подход придумал не Герман Вейль, хотя его и принято считать отцом-основателем этого направления. Это связано скорее с языковой случайностью, нежели с реальным содержанием его статей. Вейль действительно говорил о калибровочной инвариантности, однако в его работах она имеет разве что формальное сходство с трактовкой, которую в 1954 году ей дали Янг и Миллс. Именно эти ученые первыми показали, что использованите локальных калибровочных симметрий позволяет предсказывать нетривиальные физические эффекты.
Моя оценка может показаться чрезмерно строгой, но сейчас я ее поясню. Уравнения классической электродинамики можно написать как в терминах напряженностей электрического и магнитного поля, так и в терминах электромагнитных потенциалов, что, кстати, понимал и сам Максвелл. Во втором случае легко показать, что эти уравнения подчиняются одной из форм калибровочной симметрии. Однако эта симметрия становится куда более существенной при анализе движений заряженных частиц, которые описываются квантовой механикой. С уравнениями Максвелла в принципе можно работать и в том виде, в каком они заданы в терминах напряженностей электрического и магнитного полей, хотя использование потенциалов гораздо удобнее. А вот теорию, имеющую дело с поведением заряженной квантовой частицы в электромагнитном поле, без потенциалов даже невозможно сформулировать. Поэтому любую из таких теорий необходимо сделать калибровочно инвариантной.
Это обстоятельство было осознано еще в конце двадцатых годов прошлого века, причем с участием Вейля. Однако в те времена физикам еще не приходило в голову, что калибровочная симметрия лежит в самой основе квантовой электродинамики, как считают сегодня. Они полагали эту симметрию не более чем формальным следствием перехода к квантовому описанию движения заряженных частиц. Должно было пройти немалое время, чтобы увидеть в калибровочной инвариантности фундаментальный принцип, из которого, как мы теперь знаем, можно вывести гораздо больше, нежели законы квантовой электродинамики. Это совершенно новое понимание калибровочной симметрии исторически восходит к знаменитой статье Янга и Миллса. Именно они впервые показали, что из нее вытекают основные динамические свойства физической теории.
— А как Вы сами познакомились с идеями, развитыми Янгом и Миллсом?
С. В.: Я прочел их статью во второй половине 50-х годов, еще в аспирантуре. Янг и Миллс нарисовали великолепную картину, и я сразу почувствовал ее очарование. Их работе свойственна такая же красота, как и общей теории относительности, где динамика тоже выводится из свойств симметрии. Конечно, это заметили многие физики-теоретики.
Однако для физической теории мало одной лишь математической элегантности. Главная проблема модели Янга и Миллса заключалась в том, что никто не мог понять, как она и прочие модели такого же типа связаны с реальной физикой. Поля Янга и Миллса имели кванты с нулевой массой, а экспериментаторы ничего подобного никогда не наблюдали. Все дело было именно в этой безмассовости. Предположим, у вас есть теория, которая предсказывает новую частицу, однако не дает возможности вычислить ее массу. Если таковой частицы не удается обнаружить экспериментально, всегда можно предположить, что она слишком тяжела, чтобы родиться в существующих ускорителях. Но для гипотетических частиц со строго нулевой массой подобные отговорки не проходят, и нужны другие объяснения, почему их не удается обнаружить. Для модели Янга и Миллса такие причины никак не просматривались, и поэтому она долго не вызывала особенного интереса, хотя многие теоретики были с ней знакомы.
— Но в конце концов эта модель получила полное признание.
С. В.: Да, конечно. Во второй половине 60-х годов мы с Абдусом Саламом независимо друг от друга нашли первые физические приложения модели Янга и Миллса. Моя работа была опубликована в 1967 году, Салама — в 1968. Мы оба использовали механизм Хиггса, который объясняет, как спонтанное нарушение калибровочной симметрии оборачивается рождением массивных частиц. С его помощью нам удалось построить калибровочную теорию электрослабых взаимодействий, которые переносят фотоны и тройка тяжелых векторных бозонов.
Сходную теорию несколькими годами ранее развил Шелдон Глэшоу, однако он не смог справиться с проблемой массы этих бозонов. А вот нам удалось ее вычислить, причем, как потом показали эксперименты, весьма точно. Вот так и было впервые доказано, что калибровочные теории фундаментальных взаимодействий обладают реальной предсказательной силой. Использование механизма Хиггса также сделало калибровочную теорию электрослабых взаимодействий математически согласованной — в том смысле, что позволило очистить ее от бесконечностей, которые из модели Глэшоу никак не убирались.
Какова мораль этой истории? Янг и Миллс построили очень красивую математическую модель, которая в своем изначальном виде не имела реального приложения. Мы с Саламом положили ее в основу настоящей физической теории, которая со временем выдержала жесткую экспериментальную проверку. Массивные векторные бозоны были детектированы, их массы измерены, теория подтвердилась. А несколько месяцев назад было объявлено о вероятном открытии хиггсовского бозона. Массу этой частицы наша теория предсказать не могла, ее предстояло определить экспериментаторам, и они отлично справились с этой задачей. Теперь мы знаем, что она составляет приблизительно 125 ГэВ, и эта величина будет использована для многих вычислений в рамках Стандартной модели.
— Можно ли считать Вашу работу и работу Салама прямым развитием модели Янга и Миллса?
С. В.: Нет, я бы так не сказал. О слабых взаимодействиях в их статье нет и речи, о них Янг с Миллсом просто не задумывались. Они хотели с помощью калибровочных полей объяснить сильные взаимодействия, связывающие между собой протоны и нейтроны в атомных ядрах. Это и в самом деле удалось, но лишь в 70-е годы.
— И как это произошло?
С. В.: Тогда была создана квантовая хромодинамика, объясняющая свойства и структуру адронов, составных частиц, которые принимают участие в сильных взаимодействиях. Согласно этой теории, такие частицы состоят из кварков, которые скрепляют между собой калибровочные поля с безмассовыми квантами, глюонами. И тут вновь возник прежний вопрос — если глюоны не имеют массы, почему мы их не наблюдаем в чистом виде?
Многие теоретики тогда допускали, что глюоны, подобно векторным бозонам, все же обретают массу из-за спонтанного нарушения калибровочной симметрии. Как я уже говорил, этим путем их ненаблюдаемость можно было списать на слишком большие массы. Однако ни малейших разумных причин для рождения столь тяжелых глюонов так и не нашлось.
Эта загадка была разрешена совершенно неожиданным способом, который еще раз продемонстрировал силу калибровочных моделей. Дэвид Гросс, Фрэнк Вильчек и Дэвид Политцер обнаружили замечательное свойство той разновидности полей Янга — Миллса, которые работают в квантовой хромодинамике. Оказалось, что при увеличении энергии у них уменьшается эффективная константа взаимодействия. После этого Гросс с Вильчеком и я сообразили, что в таком случае при уменьшении энергии эта константа должна возрастать. Это означает, что ближнее взаимодействие между кварками и глюонами гораздо слабее, нежели дальнее. Отсюда можно заключить, что кварки и глюоны настолько сильно притягиваются друг к другу на больших дистанциях, что их невозможно наблюдать по отдельности.
Достижения теоретиков, о которых я сейчас рассказал, стали возможны опять-таки благодаря использованию калибровочных симметрий. В конечном счете они привели к созданию Стандартной модели элементарных частиц, которая дает возможность объяснить практически все результаты экспериментаторов.
— В чем Вы видите основные достоинства и слабые места калибровочных теорий фундаментальных взаимодействий?
С. В.: Хороший вопрос. Мы, физики-теоретики, на полном серьезе восприняли урок, преподанный нам Эйнштейном в 1905 году. Он понял, что природа на самом фундаментальном уровне подчиняется могущественным принципам симметрии. Эти симметрии могут полностью сохраняться или претерпевать спонтанные нарушения, но они всегда придают законам природы ту упорядочивающую простоту, которую издавна искали ученые. И мы исходили из того, что природа управляется простыми и потому познаваемыми законами. Помню, как-то я признался, что если бы фундаментальные законы природы не отличались единством, простотой и изяществом, мне было бы просто неинтересно ими заниматься. А коль скоро я это делаю, я верю, что они обладают этими качествами. И этой вере способствует та объединяющая роль, которую в сегодняшней физике исполняют калибровочные теории.
Конечно, нельзя утверждать, что в них заключена истина в последней инстанции. Стандартная модель элементарных частиц, как и любая научная теория, имеет свои пределы. Например, она утверждает, что нейтрино не должны обладать массой. Однако массы у этих частиц все же имеются, хотя и ничтожные, порядка одной миллионной массы электрона. Кроме того, в Стандартной модели нет места для частиц темной материи, какова бы ни была ее природа. И, конечно, ее главная слабость в том, что она не описывает гравитацию.
Сейчас практически все специалисты видят в Стандартной модели просто очень удачную аппроксимацию более глубокой теории, которой пока еще нет. И я вполне допускаю, что в эту теорию на фундаментальном уровне вообще не войдут калибровочные симметрии. Скажем, в структуре теории струн нет калибровочных полей, хотя их аналоги и появляются в ходе приближенного решения ее уравнений. С другой стороны, мы еще не знаем, имеет ли эта теория отношение к реальному миру. Вот и получается, что будущее калибровочных теорий пока не ясно, но в своей области применимости они работают отлично. А это совсем немало.
Я позволю себе дополнить беседу с великим физиком одним разъяснением.
В принципе, единственное различие между межкварквыми силами, которые переносятся глюонными полями, и взаимодействиями между электронами и прочими заряженными частицами, которые осуществляются посредством фотонов, состоит в том, что глюоны, в отличие от фотонов, взаимодействуют не только с кварками, но и между собой. Это различие напрямую связано с тем, что глюонные поля подчиняются иному типу калибровочной симметрии, нежели поля электрослабого взаимодействия. Именно межглюонные силы служат причиной ослабления связей между глюонами и кварками при больших энергиях (или, что то же самое, на очень малых дистанциях), о котором говорил Вайнберг.
Этот интереснейший физический эффект называют асимптотической свободой. Специфика межглюонных взаимодействий, скорее всего, объясняет и усиление межкварковых связей на больших расстояниях, вследствие чего кварки и глюоны в нашем мире не могут существовать как изолированные частицы и становятся пленниками внутри адронов (на языке физики это называется конфайнментом). Правда, при очень высоких энергиях конфаймента не существует, и кварки с глюонами могут существовать в свободном состоянии. Но такие энергии существовали во Вселенной только в первые мгновения после Большого взрыва, когда ее возраст не превышал одну микросекунду.
Алексей Левин
-
Спасибо! Прекрасная статья. Вам удалось соединить в разумных пропорциях биографию, историю физики и историю научного пути Стивена Вайнберга - крупного физика и мыслителя. "В основе законов природы должна лежать их упорядочивающая простота". Красиво. Немного жаль, что, много говоря о симметриях, вы не оформили в небольшой абзац идею суперсимметрии и её возможную связь со струнными подходами. Это была бы капелька росы на вишенке...
-
-
Наверное, я неточно выразился. Поскольку статья посвящена памяти С.Вайнберга, я хотел узнать, как он относился к гипотезам суперсимметрии и суперструн. Можно один абзац на эту тему?
-
Вайнберг на полном серьезе рассматривал использование суперсимметрии для решения космологических проблем. Можете заглянуть в его книгу "Космология", она есть в русском издании. Он также видел в теории суперструн единственную надежду на создание объединенной модели всех четырех фундаментальных взаимодействий. Однако он подчеркивал, что эта теория прогрессирует медленно и ее грядущий успех пока не гарантирован.
-
Спасибо, обязательно загляну. Я только что в соседней ветке написал пост о том, что развитие ФЭЧ упёрлось в космологию, и чтобы достичь прогресса, обеим наукам нужно развиваться согласованно. Ведь, космология - это пространство, а ФЭЧ - это энергия, причем, масса-энергия. Как пространство может переходить в массу-энергию? Или нужно ставить вопрос наоборот: как энергия может переходить в пространство? Струнная теория идет от исходной порции энергии, постулировав ее в виде струны или петли. Получается, количества ещё нет, а форма уже приготовлена. С философской стороны это не есть хорошо... Может, потому и "прогрессирует медленно"?
-
Вайнберг как раз и считал, что максимального прогресса можно добиться на пути синтеза теории элементарных частиц с астрофизикой и космологией. И так сейчас думают многие.
-
Книгу скачал, полистаю. Очень интересно, как крупный, очень крупный физик подошел к философскому, по сути, вопросу о начале всего. Струнщики полагают, что в точке 0 первая капля энергии появилась уже в определенной пространственной форме. То есть, струна - как форма пространства,- появилась раньше и ждала появления кванта энергии, чтобы соединиться с ним. А почему не наоборот? А, может, они выделились вместе из чего-то предшествующего? Ну, посмотрим, удастся ли мне понять подход Вайнберга из его могучего трактата... Ещё раз спасибо, Алексей!
-
Вайнберг как раз и считал, что максимального прогресса можно добиться на пути синтеза теории элементарнх частиц с астрофизикой и космологией. И так сейчас думают многие.
Теории элементарнх частиц, в том числе Вайнбергом, доведена до пределов своего совершенства, как в позапрошлом веке периодическая система химических элементов.
https://ru.wikipedia.org/wiki/Периодическая_система_химических_элементов
.Разработанная в XIX веке в рамках науки химии, периодическая таблица явилась готовой систематизацией типов атомов для новых разделов физики, получивших развитие в начале XX веке — атомной физики и физики ядра.
Стандартная модель может служить только ориентиром, частным случаем и ограничением для новых разделов физики.
Смогут ли физики-ядерщики описать вселенную без материи, в том числе темной, там где полная барионная симметрия, нет места для Стандартной модели, и нет ничего кроме фотонов?
Это будет похоже на попытки алхимиков превратить ртуть в золото, без использования ядерного реактора :)
-
-
-
-
-
-
Однако массы у этих частиц все же имеются, хотя и ничтожные, порядка одной миллионной массы электрона.Извините, но это никем не доказано от слова совсем. Это просто голое предположение.
-
Ну, почему же? В эксперименте надежно доказано существований нейтринных осцилляций. Они возможны только в случае, если массы хотя бы двух (а скорее всего всех трех) ароматов нейтрино не равны нулю. Есть довольно надежное ограничение на сумму масс всех трех ароматов нейтрино, основанное на анализе структуры реликтового излучения и других космологических соображениях. По этой оценке, она не должна превышать 0,2 эВ. По порядку величины это как раз миллионная доля массы электрона.
-
Спасибо! Действительно крутая статья! Истинное наслаждение.
Не могли бы вы чуть раскрыть механизм обретения массы нейтрино? Вот здесь вы намекаете, что в общих чертах причина массы у нейтрино просматривается: "[Хиггсовский механизм] оказался полезным и для понимания массы нейтрино (хотя для нее есть и другое объяснение)". И есть ли хоть одна другая частица с того же порядка массой покоя? Или нейтрино стоят совершеннейшим особняком?
P.S. Истиноv'а комментарии неинтересны. Так много прилагательных "голое предположение", "совсем" и т.п. здесь и в других ветках. Безграмотный, неумный комментатор, увы-
Это очень непростой вопрос. В рамках Стандартной модели масса нейтрино строго равна нулю. Однако есть возможность ее ввести в теорию, если предположить, что существует другая разновидность нейтрино, которая полностью тождественна своему антинейтрино. Эту возможность в конце 1930-х рассмотрел Этторе Майорана, очень талантливый итальянский физик-теоретик с очень трагической судьбой. При таком раскладе появляется способ объяснить, почему масса "обычного" нейтрино отлична от нуля, но при этом очень мала. Согласно этой схеме, она обратно пропорциональна массе майорановского нейтрино, которая чрезвычайно велика, не менее 1000 ТэВ. Однако существование элементарных фермионов майорановского типа пока не доказано. Конечно, фотон - сам себе античастица, но его спин равен единице, а не половине, как у нейтрино.
По малости массы нейтрино и в самом деле не имеют себе равных. Правда, теоретики довольно давно изобрели гипотетическую частицу аксион с массой не более 15 эВ. Ее существование выглядит довольно вероятным, но в эксперименте она не обнаружена.-
Извините, но вы пишете об этом так, что может сложиться впечатление, будто для введения массы нейтрино в СМ нужно поменять какой-то основополагающий принцип, в то время как механизм, о котором вы пишете, получается в общем-то автоматом, если предположить, что нейтрино, как и все остальные фермионы СМ, есть не только левые, но и правые. Кстати, дираковские нейтрино, насколько я знаю, еще не закрыты (хотя их малая масса и выглядит странно). Ну т.е. я бы подчеркнул, что проблема не в каком-то принципе построения СМ и ее обобщить на массивные нейтрино легко, а в том, что мы не знаем деталей, как именно масса эта появляется. И не знаем, можно ли обойтись простым обобщением СМ (причем не знаем сколько правых нейтрино надо добавлять) или это эхо какой-то принципиально новой физики на больших энергиях.
-
-
-
По определению, масса частицы не зависит от ее динамического состояния. Выражение "масса покоя" - дань архаичной терминологии. Масса фотона строго равна нулю, другой у него нет. Именно поэтому у фотона две поляризационные степени свободы, а не три, как у любой массивной частицы.
-
это, опять же, смотря о какой массе идет речь. о массе-энергии, заключенной в частице или о грави-инертной, которая, кстати, зависит от динамического состояния частицы.
По определению, масса частицы не зависит от ее динамического состояния
А как же релятивистская масса?
Фотон не бывает в состоянии покоя. Поэтому массы покоя у фотона нету по определению. Но отклонение фотона в гравитационном поле имеет место быть.-
Фотон отклоняется в гравитационном поле из-за искривления пространства-времени. Гравитация - это и есть физическое выражение такого искривления. Фотоны как раз в силу своей нулевой массы всегда движутся по геодезическим траекториям, которые в искривленном пространстве-времени отличаются от прямых линий. Что до релятивисткой массы, то это просто условное обозначение полной энергии частицы.
-
-
У фотона нет массы, но гравитирует не масса, которая является только мерой инерции, а тензор энергии-импульса, который у фотона не равен нулю. Фотон не может создавать скалярную кривизну, однако он всё равно искривляет пространство сложным образом как и всякий объект имеющий тензор энергии-импульса и соответственно, реагировать на гравитацию.
-
-
Пфффф.... Фотон гравитирует, еще как. Смотрите хотя бы линзирование света около звезд. В ОТО вообще нет понятия массы ни в каком виде, масса к гравитации вообще не имеет никакого отношения и соответственно, в гравитации не участвует. Нет таких понятий как масса-энергия и гравитационная масса, масса вообще одна единственная.
-
-
Потому что она чисто гипотетична, никакой темной материи никто никогда не видел, видели только гравитацию.
И это не ошибочное представление. С квантовой гравитацией ничего не выходит только потому что ее просто не существует в природе.-
-
Если вы не знаете элементарной физики, то зачем спорите?
Это элементарные знания ОТО - и я вам это уже писал - искривляет тензор энергии-импульса, в нем нет массы.
В СТО вообще нет гравитации ни в каком виде, это по существу теория света. В ОТО нет массы ни в каком виде, это теория только гравитации.-
-
Ты не обучаем детеныш. И читать не умеешь, с такими умственными с iQ стремящимся к нулю способностями троллить в дискуссиях запрещено.
Ты физику даже на уровне школы не знаешь. И русского языка не понимаешь, я тебе это очень серьезно говорю о твоих нижайших умственных способностях. Ты даже не можешь понять разницу в словах тензор энергии-импульса и 4-импульс. Тензор энергии импульса определяется без понятия массы, у электромагнитного излучения нет массы ни в каком виде, а тензор энергии-импульса есть. Тензор энергии-импульса вообще в своей формуле не имеет масс в ОТО, он в ОТО определяется только через тензор метрики.
Ты туп, у фотона есть импульс, но нет массы. Так что это ты бессмысленный. И не спорь, то что ты не знаешь даже школьную физику поэтому омерзительно троллишь. Таким образом скоро из яслей будут опровергать что 2*2 = 4. Поколение гугл блин, вся информация урывками, с викистраниц читается не более одного предложения найденного гуглем, никакого регулярного образования.
-
-
-
-
-
-
-
-
-
-
-
-
-
А у нейтрино одно поляризованное состояние, вместо двух как требуется для массивных фермионов. Кстати, если есть масса, то частица может двигаться с любой скоростью, но всегда меньше скорости света, и иметь покой. Однако никто никогда не видел покоящегося нейтрино. Более того, в космических измерениях пучки нейтрино от космических событий всегда приходили строго синхронно с пучками фотонов. То есть они оба двигаются только со скоростью света.
-
-
А что СТО? В СТО масса есть, но массы покоя нет. Там энергия покоя.
В своей системе отсчета фотон стоит, к нему понятие скорости не применимо. Сам себя фотон наблюдать не может, да и никакого другого.-
-
Еще раз, ничего подобного. Это скажем так устаревшие объяснения для детишек. Да были времена когда таким термином пользовались для упрощения, но сейчас не пользуются. потому что такого понятия как масса покоя в физике нет, есть просто масса. Тут фишка в том что масса выражается в энергетических единицах, поэтому энергия покоя выражает массу в МэВ. То есть энергия покоя это тоже самое что масса, отсюда и возникло словосочетание масса покоя и релятивистская масса, то есть полная энергия при движении.
Гугл вам не в помощь, учитесь читать дальше "Согласно концепции эквивалентности массы и энергии, инвариантная масса эквивалентна энергии покоя, в то время как релятивистская масса эквивалентна релятивистской энергии (также называемой полной энергией)".
Масса в СТО всегда неизменна и она одна, именно из этой никогда неизменной величины выражается энергия, как покоя так и полная энергия. Описание по другому это уже архаика связанная с устаревшими ошибочными представлениями.
-
-
-
-
В каком смысле не доказано? Это утвеждение следует из уравнений Стандартной модели. А ее пока никто не отменял.
-
Там нет следования, поскольку нейтрино взаимодействует с векторными бозонами слабого взаимодействия, которые имеют массу, вот по этой причине может быть осцилляция.
-
Проще говоря:
https://ru.wikipedia.org/wiki/Нейтринные_осцилляции
*Нейтринные осцилляции в веществе обусловлены наличием у нейтрино эффективной массы в среде, ненулевой независимо от наличия у нейтрино массы.
Но судя по всему эффективной массы (эффекта МСВ) не достаточно для описания осцилляций:
https://elementy.ru/novosti_nauki/432226/Polucheny_pervye_nameki_na_effekt_MikheevaSmirnovaVolfenshteyna_pri_dvizhenii_n eytrino_skvoz_Zemlyu -
Вам чтобы были хоть какие-нибудь осцилляции надо, чтобы нейтрино разных поколений как-нибудь отличались друг от друга, иначе все переходы типа e_i + W+ -> sum_j V_ij nu_j в итоге ведут к абсолютно одинаковой физике нечувствительной к матрице V. Все калибровочные взаимодействия в стандартной модели абсолютно слепы к номеру поколения и различаться они могли бы только массами. Безмассовые нейтрино и с материей взаимодействовали бы абсолютно одинаково и никакие эффективные массы к осцилляциям бы не привели.
-
Стандартная модель не истина в последней инстанции, не забывайте. Это всего лишь какое-то преближение. И кстати, большинство массы берется не из бозонов Хигса, как утверждает стандартная модель. Хиггсы обеспечивают всего лишь несколько процентов общей массы частиц.
Массы в стандартной модели заданы извне, она их не описывает, да порой очень хитро через некие углы поворота из-за чего кажется что она их вычисляет, но дело в том что эти углы сами чисто внешние параметры.
Еще раз, не масса обеспечивает взаимодействие с материей, а взаимодействие обеспечивает внутреннее свойства частиц.-
Законы Ньютона тоже приближение. Но когда они работают, они работают и вы их просто так не обойдете.
Если вы о том, что большая часть массы адронов берется из сильного взаимодействия, так это как раз стандартная модель и говорит. И к лептонам это не имеет никакого отношения - у них масса берется как раз от Хиггса. Про тау у нас яркое экспериментальное подтверждение - константа взаимодействия с Хиггсом четко соответствует предсказанной в Стандартной модели (как и для t и b кварков).
Что все трудно, непонятно ничего и потому все "очень хитро через некие углы поворота"? Зачем позориться-то, если врубиться не получается, не понимаю. Это даже интересно, что за угол поворота здесь всплыл, угол Вайнберга, упомянутый в тексте выше? Представьте себе, угол Вайнберга вычисляется из соотношения констант связи калибровочных взаимодействий, это не какой-то независимый параметр.
-
-
-
Общая причина феномена осцилляций состоит в рассогласовании между собственными состояниями частиц, обусловленными слабым калибровочным взаимодействием, и массовыми состояниями, связанным с полями Хиггма. Такое рассогласование наблюдается не только в лептонном секторе, где оно порождает осцилляции нейтрино, но также и в кварковом. У нейтрино осцилляции проявляется в смешении ароматов, а у кварков - в "качаниях" нейтральных мезонов от частиц к античастицам. В общем, это очень интересный эффект, изучение которого, вероятно, принесет еще немало сюрпризов.
-
Все калибровочные взаимодействия в стандартной модели абсолютно слепы к номеру поколения и различаться они могли бы только массами.
Удивительно.
Раньше физики допускали существование разных нейтрино с одинаковой нулевой массой.
Где можно найти публикации об этом перевороте в ядерной физике?-
Какой именно переворот вас интересует? Было отношение, что может безмассовые, может нет. Что нейтрино несколько сортов (которые в слабом взаимодействии превращаются преимущественно в разные виды заряженных лептонов) известно с начала 60х годов. Про осцилляции нейтрино спекуляции шли, опять же, с начала 60х. В 70е уже вовсю обсуждались возможные механизмы генерации их масс в свете недавно созданной Стандартной модели. При этом, никакого противоречия в модели с безмассовыми нейтрино нет, в некоторых попытках расширения Стандартной модели (типа самой первой модели великого объединения) они и должны были бы быть безмассовыми, потому почему бы и не допускать.
-
Разные сорта нейтрино взаимодействуют с материей по разному. Это факт.
При этом Вы утверждаете:Безмассовые нейтрино и с материей взаимодействовали бы абсолютно одинаково
То есть Вы исключаете возможность существования безмассовых нейтрино.
И одновременно Вы допускаете возможность существования безмассовых нейтрино:При этом, никакого противоречия в модели с безмассовыми нейтрино нет
Никак не соображу как разгадать эту загадку.
Может тут всю модель менять надо?
-
-
-
-
-
Последние новости








_390.jpg)













Стивен Вайнберг (1933–2021) в своем кабинете. Фото 2008 года с сайта news.utexas.edu