Закон всемирного тяготения действует и в миллимасштабе

Австрийские физики провели эксперимент по измерению гравитационного притяжения очень маленьких тел — золотых шариков массой 90 миллиграммов и диаметром 2 миллиметра. Оказалось, что такие маленькие тела, находящиеся на расстоянии всего нескольких миллиметров друг от друга, тоже притягиваются по классическому закону всемирного тяготения Ньютона. Проверка этого закона на таком масштабе масс и расстояний проведена впервые. Авторы эксперимента надеются, что в перспективе разработанная ими методика регистрации очень слабого тяготения между шариками позволит нащупать границу, за которой в полной мере проявляются эффекты квантовой гравитации.
Вспомните простую фразу, которую многим приходилось заучивать почти до автоматизма в школе: «любые два тела во Вселенной притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними». К этой фразе прилагалась формула
\[F=\frac{GMm}{R^2},\]в которой \(M\) и \(m\) — массы тел, \(R\) — расстояние между ними, а \(G\) — коэффициент пропорциональности, который называют гравитационной постоянной. Это — закон всемирного тяготения Ньютона. Но к нему стоит сделать несколько дополнений, которые обычно в школе упускают.
Во-первых, эта формула верна не для любых тел, а только для точечных — то есть таких, что их размеры много меньше расстояния между ними. Формула, правда, верна и для тел, обладающих сферической симметрией, но это потому, что сумма сил, действующих со стороны точек сферического тела на пробную массу, оказывается точно такой же, как если бы вся масса тела была сосредоточена в его центре. Поэтому для планет, звезд и их спутников (естественных и искусственных) этот закон вполне хорошо работает (подтверждением чему служит открытие Нептуна Иоганном Галле в 1846 году, ставшее возможным благодаря обсчету наблюдавшихся аномалий в орбитальном движении Урана, выполненному Урбеном Леверье; подробности этой истории можно прочитать в статье Алексея Левина Охота на планету: Нептун).
Во-вторых, эта формула работает только в так называемом приближении слабого поля, — когда можно пренебречь эффектами общей теории относительности. Обычно это означает, что вторая космическая скорость для каждой из упомянутых масс должна быть сильно меньше скорости света, равно как и сами эти массы не должны двигаться относительно друг друга с релятивистской скоростью. Например, навигационные спутники на околоземной орбите движутся со скоростями несколько километров в секунду, чего уже достаточно для того, чтобы для них закон всемирного тяготения в классической формулировке не работал в точности. В середине XIX века нарушение его работы было замечено (все тем же Леверье) в орбитальном движении Меркурия: перигелий его орбиты поворачивался относительно звезд быстрее, чем это предсказывала теория, опиравшаяся на закон Ньютона (см. Смещение перигелия Меркурия). Это расхождение послужило одной из важных причин для создания в начале XX века общей теории относительности (см. Столетие ОТО, или Юбилей «Первой ноябрьской революции», «Элементы», 25.11.2015).
В-третьих, утверждение о том, что этот закон работает всегда и везде — это экстраполяция. Это утверждение, собственно, и принадлежит Ньютону (хотя сама формула, приведенная выше, была получена еще до него — скорее всего, другим англичанином, Робертом Гуком). Гений Ньютона заключался в том, что он не побоялся предположить, что яблоко падает на землю, влекомое той же самой силой, которая не позволяет Луне улететь в космическое пространство. И тем самым распространить явление гравитации действительно на все тела во Вселенной.
Но любая экстраполяция, тем более такая смелая, требует проверки и экспериментальных подтверждений.
Классические опыты по проверке закона Ньютона провел в конце XVIII века еще один его соотечественник Генри Кавендиш. Это был прямой опыт, в котором проверялось притяжение двух пар свинцовых шаров с массами 160 и 0,8 кг, находящихся на расстоянии 23 см друг от друга (см. Эксперимент Кавендиша). Меньшие шары устанавливались на крутильных весах — коромысле, подвешенном на медной нити. Сила гравитационного притяжения между шарами противодействовала упругой силой скручивания нити. Целью эксперимента Кавендиша было измерение плотности Земли. Но по факту он измерял величину гравитационной постоянной. Она оказалась довольно мала — в единицах системы СИ ее современное значение составляет
\[G=(6{,}67430\pm0{,}00015)\cdot10^{-11}\ \frac{\text{м}^3}{\text{кг}\cdot\text{с}^2}.\]Это очень маленькое значение, и оно показывает, насколько слабо тяготение.
После того, как были открыты три других фундаментальных взаимодействия — электромагнитное и два ядерных, — эта слабость только подтвердилась. И она создает если не трудности, то — уж точно — вызовы физикам и в наши дни.
Мы можем хорошо проверить действие закона Ньютона на планетах и звездах. Расстояния между ними огромны, но их массы настолько велики, что силы притяжения, которые между ними действуют, тоже огромны и порождают хорошо регистрируемый эффект. Но очень сложно проверить этот закон на маленьких массах, находящихся близко друг к другу.
Дело в том, что сделать это мы можем только в точных земных экспериментах (астрономические наблюдения тут, понятно, не помогут). Так, например, свинцовые шары в эксперименте Кавендиша притягивались друг к другу с силой \(10^{-7}\) Ньютонов. C такой силой наша планета притягивается к другой подобной планете, расположенной, скажем, в галактике NGC 55 (на расстоянии 2 Мпк от нас), то есть практически совсем не притягивается. Поэтому установка Кавендиша была заключена в деревянный кожух, который защищал ее от внешних воздействий (например, легчайших потоков воздуха). Перемещение коромысла за счет тяготения составляло всего лишь несколько миллиметров, и должно было быть измерено с точностью порядка 0,1 мм. Да и само коромысло не оставалось зафиксированным. Оно участвовало во вращательных колебаниях с периодом около 10 минут. Все это усложняло (и, что самое интересное, усложняет по сей день!) прямое измерение гравитационных сил. Но человеческая изобретательность преодолела (и преодолевает) эти препятствия.
Эксперименты по измерению гравитационной постоянной (об сложностях, которые там возникают, читайте в новости Новые измерения гравитационной постоянной еще сильнее запутывают ситуацию, «Элементы», 13.09.2013) и зависимости силы тяжести от масштаба — одни из самых сложных в физике. Об этом красноречиво говорит тот факт, что гравитационная постоянная среди всех фундаментальных констант на данный момент определена с наименьшей точностью. А в каком-то смысле эта серия экспериментов — еще и одна из самых долгих, ведь она длится уже больше двух веков. В наши дни ученые, вооруженные современной прецизионной техникой «ищут» притяжение на примере все меньших тел, расположенных все ближе друг к другу и притягивающихся все слабее и слабее.
К сегодняшнему дню удалось добиться проверки закона всемирного тяготения (конкретнее, квадратичного спадания силы притяжения с расстоянием) вплоть до масштабов расстояния 50 микрометров (J. Lee et al., 2020. New Test of the Gravitational 1/r2 Law at Separations down to 52 μm). Но в подобных экспериментах всегда участвовали вполне «обычные» массы, измеряющиеся десятками или сотнями килограммов или, реже, десятками граммов. Или же вообще речь шла о поведении маломассивного тела в поле тяготения Земли (то есть в роли одного из экспериментальных тел выступала целая планета).
Но в недавнем эксперименте, результаты которого были опубликованы в недавнем выпуске журнала Nature, ученым удалось зафиксировать притяжение золотых шаров диаметром 2 мм с массами всего 90 мг, отнесенных на расстояние 1 мм друг от друга. Согласно ньютоновской формуле, между ними действовала сила порядка \(10^{-13}\) Ньютонов. С такой силой наша Земля притягивает другую такую же планету, расположенную уже на гигантском космологическом расстоянии в 5 Гпк! К слову, диаметр всей видимой нам Вселенной составляет всего 28 Гпк.
Впрочем, о далеких планетах волноваться экспериментаторам надо было явно не в первую очередь, поскольку человек, стоящий в 2,5 метрах от установки, оказывает на эти шарики такое же по силе гравитационное воздействие. Но если от этого воздействия деться было некуда (гравитация не экранируется), то другие факторы, создающие шумы в эксперименте, авторам необходимо было как-то сводить к минимуму. Так, эксперимент проходил в глубоком вакууме, под давлением 10−9–10−10 атм., чтобы уменьшить воздействие от молекул воздуха. Вся установка располагалась на тяжелом оптическом столе, который, впрочем, чувствовал мелкие сейсмические колебания («несмотря на сравнительно спокойную предрождественскую пору в городе», как отметили авторы). Эти колебания контролировались чувствительными сейсмодатчиками, показания которых учитывались в анализе. Наконец, золотые пробные массы необходимо было освободить от электростатического заряда, разрядив их до уровня около 100 тысяч элементарных зарядов (то есть из ~3·1020 атомов золота в шарике, только 100 тысяч имели дополнительный заряд), а также установить экран Фарадея между массами.
Поэтому, быть может, не менее важным результатом эксперимента стало создание измерительной технологии, которая позволила отсечь паразитные воздействия от других тел (в том числе электромагнитные). Шары не просто подносились друг с другу на маленькое расстояние. Один из них периодически двигался вперед-назад с периодом 79 секунд (частотой 12,7 мГц), создавая периодическое воздействие на второй. А тот, подвешенный на свободном балансе, приобретал из-за этого периодическое ускорение, причем именно такое, какое и ожидается от силы, спадающей по закону обратных квадратов. Хотя, как понятно из описания выше, колебания пробного шара в большей степени определялись именно внешними факторами, но, на некоторых отдельных частотах они определялись именно силой гравитации, действующей со стороны второго шарика (как это видно из рис. 2). В чем-то эксперимент был похож на покупку иголки, завернутой в стог сена.

Рис. 2. Спектр колебания подвеса (показан синим). Большая часть компонентов этого спектра определяется внешними факторами (сейсмическими, тепловыми, воздействием от экспериментаторов и т. д.). Но на двух частотах (показаны красным) основной вклад в спектр дает именно гравитационная сила от пробной массы. Изображение из обсуждаемой статьи в Nature
В качестве дополнительного результата исследователи измерили и значение гравитационной постоянной:
\[G=(6{,}04\pm0{,}06)\cdot10^{-11}\ \frac{\text{м}^3}{\text{кг}\cdot\text{с}^2},\]что, с учетом систематических погрешностей, известных экспериментаторам, статистически неотличимо от принятой на сегодня величины. Хотя...
Хотя статистика, как известно, не отвечает ни на какие поставленные вопросы. Она только преподносит информацию к размышлению. Ранее было подмечено, что чем меньшие массы используются в эксперименте по измерению G, тем меньше, в среднем, получается ее значение. Этот эффект совершенно незначим и сегодня к нему стоит относиться как к просто забавному стечению обстоятельств (но, по-моему, весьма интересному). К слову, из трех десятков отдельных измерений, которые были проведены в обсуждаемой работе, величина G оказывалась больше общепринятой только в трех случаях — в остальных она всегда оказывалась систематически меньше (рис. 3).

Рис. 3. Результаты измерений гравитационной постоянной G, проведенных в ходе нескольких этапов эксперимента. В среднем полученные значения оказались меньше принятого «стандартного» значения CODATA. Изображение из обсуждаемой статьи в Nature
Впрочем, исследователи и не ставили перед собой задачу еще раз уточнить G. И, более того, не стоит думать, что подобные эксперименты нужны только для того, чтобы убедиться в том, что гравитация «и вот на этих масштабах тоже работает». В такой формулировке они становятся похожими на спорт, причем бесконечный — можно надолго себя обеспечить работой (ну и финансированием, куда же без него), просто постоянно меняя масштабы задачи.
В действительности же, интересно не подтвердить известный закон в очередной раз, а наконец найти, где же он перестает выполняться. У любой физической модели есть свои границы применимости (вспомните ту же общую теорию относительности, которая пришла на смену ньютоновской «силе тяготения», когда начали изучать тонкие эффекты динамики тяжелых и быстрых объектов). И зачастую эти границы приходится буквально нащупывать, продвигаясь в пространстве параметров эксперимента практически вслепую.
Обсуждаемая работа — еще один важный шаг по нащупыванию «микрограниц» применимости ньютоновской теории гравитации. И, как уже говорилось, создание технологии исследования гравитации для малых масс (с осциллирующей массой, системами экранировки, лазерной метрологической системой и т. д.), быть может, не менее важный результат этой работы. Сами авторы считают, что их метод может быть распространен далее разумным образом для проверки закона тяготения уже для масс, порядка планковской (\(m_{Pl}\approx2\cdot10^{-5}\) г). Для этого необходимо, чтобы колебания системы, возникающие под воздействием движущейся массы, не затухали слишком быстро. Это определяется добротностью системы Q (можно сказать, что это количество циклов, за которые колебания затухают полностью). Добротность обсуждаемого эксперимента составляла 4,9. А работа с планковской массой будет возможна при добротности Q = 20 000.
Откуда известно, что в какой-то момент закон всемирного тяготения в том виде, к которому мы привыкли, действительно должен перестать работать? Дело в том, что, углубляясь в микромир, однажды мы экспериментально подойдем к тому пределу, на котором начинают работать эффекты квантовой гравитации. Это та граница, за которую ученые пытаются продвинуться — пока безуспешно — как в экспериментах, так и в теории. Вопрос, на который теория квантовой гравитации должна отвечать таков: как устроено гравитационное взаимодействие настолько малых систем, для которых уже существенны квантовые эффекты? Например, их нужно учитывать для описания частиц темной материи или сверхплотной материи в центре нейтронной звезды (или даже в центре черной дыры, что бы там ни скрывалось за термином «сингулярность»). Вероятно, без их учета не обойтись и при разработке новой микроэлектроники (которая со временем, быть может, станет фемто- или даже аттоэлектроникой).
А еще гравитация на малых масштабах — это и возможные дополнительные измерения. Можно считать, что квадрат расстояния между телами в формуле закона Ньютона связан с трехмерностью нашего пространства. И в пространстве большей размерности этот показатель степени вполне мог бы оказаться другим. Например, если наш мир действительно многомерен, но некоторые измерения имеют очень маленький масштаб (как это предполагает теория струн), то есть шанс это заметить, проводя как раз такие эксперименты.
Вот поэтому, казалось бы, школьный эксперимент, «уменьшенный» в несколько тысяч раз по массам и расстояниям, в действительности стал серьезным и интересным научному сообществу исследованием.
Источник: Tobias Westphal, Hans Hepach, Jeremias Pfaff & Markus Aspelmeyer. Measurement of gravitational coupling between millimetre-sized masses // Nature. 2021. DOI: 10.1038/s41586-021-03250-7.
Антон Бирюков
-
"...золотых шариков массой 90 миллиграммов и диаметром 1 миллиметр... Авторы эксперимента надеются, что в перспективе разработанная ими методика регистрации очень слабого тяготения между шариками позволит нащупать границу, за которой в полной мере проявляются эффекты квантовой гравитации..."
Ржунимагу... Думаю, даже объяснять тут ни к чему, почему этим утром это главный анекдот.
В целом же вопрос остаётся. Интересно, почему сразу же после признания этого закона его не подвергли критике, ведь очевидно же, что при уменьшении расстояния сила тяготения возрастает до бесконечности. Бесконечности, Карл! И это ещё не всё. В любом теле в центре существует такая точка - центр масс. С бесконечной, согласно формуле, гравитацией.
Сегодня мы знаем, что появление бесконечности, сингулярности, тахионов свидетельствует явно о сбое теории в данной области применимости, но очень даже совсем недавно (в отношении Эйнштейна) это было не так.-
>очевидно же, что при уменьшении расстояния сила тяготения возрастает до бесконечности
Для точеченых масс — да. Но не менее очевидно, что точечная масса — уже содержит в себе бесконечную плотность. Garbage in — garbage out, на малых расстояниях неприменима именно модель точечной массы. В частности, при рассмотрении силы тяжести внутри тела. Для распределённых масс всё в порядке, и физики даже во времена Ньютона вполне это понимали.
>И это ещё не всё. В любом теле в центре существует такая точка - центр масс. С бесконечной, согласно формуле, гравитацией.
К тому же пункту. "Согласно формуле" в центре сферически симметричного объекта сила равна нулю. Разумеется, если эту формулу правильно применять. В центре масс несимметричного объекта — уж какая выйдет, нужно честно интегрировать.
Вас, вероятно, ввела в заблуждение фраза о поле сферически симметричных объектов. Она корректна, но для силы снаружи от них. Для силы внутри нужно рассматривать массу, заключённую внутри сферы радиуса R — масса снаружи вклада не даёт. В случае постоянной плотности масса внутри ~R^3, а значит сила ~R и убывает к нулю в центре.
Строго это выводится из теоремы Остроградского-Гаусса, но может быть продемонстрировано и "на пальцах".-
Очень достойно Вы ему г... на ж... натянули. Я восхищен!
Дамский вопрос: можно ли применить теорему О-Г к пространству внутри СМЧД? Вроде как у космологов общим местом является то, что внутри её, в центре, находится сингулярность, которая возникает как раз потому, что сила там возрастает. А с чего бы ей возрастать-то? Или что?-
вопрос не ко мне, но встряну, так как давно тоже этим вопросом интересуюсь )
С первым по поводу глаза и ж., согласен )
По второму – я так понимаю, там не в том дело что внутри СМЧД сила возрастает и поэтому есть сингулярность (а что это? никто не знает), а в том, что нет пока научной теории или модели достоверно описывающей пространство внутри ЧД (а есть ли оно там?). ОТО там не работает, например. Время и пространство меняются местами. А по ее формулам объем вещества равен нулю, не стремится, а строго ноль. То есть плотность бесконечна? Но как? Масса же конкретна. Не работает. Взяли и заменили "мы не знаем" на "сингулярность". Могу ошибаться, я аматор.
Хотя мне нравится гипотеза планковского вещества и планковских звезд (можно в вики почитать).
-
-
-
-
Ну, я бы доказывал так:
1. Поток поля от точечного заряда через сферу любого диаметра постоянен 4piGM — прямо следует из формулы.
2. Если мы выберем кусок сферы и сместим его, сохраняя угловой размер, поток не изменится — через смещённый кусок он тот же, а через боковые стенки нулевой, так как поле направлено по радиусу.
3. Любую поверхность, охватывающую точечный заряд можно приблизить такой "ступенчатой сферой", с произвольной точностью, и поток останется тем же.
4. (Вот здесь враньё, вернее, правда, но нужно доказывать). Значит и поток через любую поверхность тот же, 4piGM.
5. Поле линейно складывается, значит и поток через любую поверхность от любого количества точечных масс внутри неё равен 4piG*(M1+M2+...).
6. (Тоже нужно доказывать.) Значит и поток через любую поверхность для любого распределения масс внутри 4piGM, где M — полная масса внутри поверхности.
7. В случае сферической симметрии у поля может быть только радиальная компонента Fr, которая постоянна на поверхности сферы, и её поток равен площади сферы * массу внутри сферы. Значит, когда внутри сферы нет массы, то и поля на её поверхности нет.
Отмечу, что если сферической симметрии нет, то полный поток нулевой, а вот поле нет, просто где-то оно входит через поверхность, а где-то выходит — локальный поток входит со знаком, зависящим от направления. Скажем, внутри полого куба поле будет. Ближе к центру грани она направлена к грани, ближе к углу — внутрь куба.
-
-
Не надо приплетать к ньютоновскому закону в применении к несчастным макрошарикам эффекты квантовой гравитации. 1 мм и 10 в минус 33 см - как-то уж очень трудно уместить "на одном графике". Я понимаю, что очень хочется, но связи так и не видно.
Если формула Ньютона неверна, почему она в учебниках и почему хотя бы не сказано об области применимости?
А вот с эйнштейновской теорией похоже нет особых проблем. Внутри шарика, в центре, нет сингулярности с бесконечной гравитацией. Не чёрная дыра, массы не хватит для создания сингулярности. Поэтому и два шарика не могут притягиваться с бесконечной силой, которая согласно формуле Ньютона должна непрерывно возрастать по мере их сближения вплоть до сжатия обоих в точку.
Вообще, все эти взаимные притяжения двух шариков - всё та же нелепая ньютоновщина, базирующаяся на явно глючной формуле. Вот, Альберт наш понял бы меня, у него другое мышление. Нет ничего в этой истории, кроме геометрии пространства, порождённой массой. Есть шарик, прогнувший вокруг себя пространство на столько, на сколько смог. Милости просим в "яму" другой шарик (справедливости ради, тоже пытающийся организовать свою яму). Насколько они оба "поработают" над совместной "ямой" своими тушками, таково и тяготение будет. До квантовой гравитации там ой как далеко.
"Теория" как-то не складывается. Для ответа на мои школьные вопросы школьных же знаний и хватит.
Да и австрийцы собственно ничего интересного не нашли. Шарики притягивались! Моё ржание касалось попытки приплести туда эффекты квантовой гравитации. :-)))
-
Область применимости теории гравитации Ньютона - грав. потенциал
|phy| << c^2.
Т.к. потенциал мы всегда считаем относительно чего-то, то можем попробовать даже "почти возле границы" сингулярности построить некоторую небольшую область и описать её ... с помощью СТО.
Вариант учета СТО в слабых грав. полях у нас тоже есть:
https://ru.wikipedia.org/wiki/%D0%93%D1%80%D0%B0%D0%B2%D0%B8%D1%82%D0%BE%D0%BC%D0%B0%D0%B3%D0%BD%D0%B5%D1%82%D0%B8%D0%B7 %D0%BC
И, как я понимаю, один из "постулатов" для вывода уравнений ОТО - "нам нужно получить такие уравнения, чтобы они давали в пределе слабых грав. потенциалов и малых относительных скоростей механику и гравитацию Ньютона".
При желании Вы конечно можете построить теорию, которая будет давать немного другой предел, лишь бы сошлось со всеми наблюдаемыми данными.
Вопрос – если точность повышается с 10 в минус 7й Ньютонов до 10 в минус 13й – есть ли конкретная грань в цифрах, которой нужно добиться, чтобы ответить - свернутые измерения Калаби-Яу есть или их нет, пространство на сверхмалых масштабах перестает быть трехмерным или не перестает? Заранее благодарен за ответ.
-
Имхо, с точки зрения гравитации очень сложно заметить эти "дополнительные измерения". Если бы было ЭМ взаимодействие частиц - было бы "чуток" проще.
Если мы сможем представить струну, которая "изгибается" в 9-измерениях, в 6 из которых размер (и, по идее, отклонение от точки равновесия) имеет порядок длины Планка... И наверное законы ЭМ взаимодействия будут выглядеть немного не так, когда энергия взаимодействия 2 зарядов
|U| = k*q1*q2/r >~ M(Z)*C^2 - энергии покоя Z-бозона.
Так что автор заметки поторопился с вами соглашаться. Шарики либо точно были не полыми, либо размер или масса указаны неверно. Шар радиусом 1 мм весил бы около 81 мг, диаметром 1 мм - еще в восемь раз меньше. А если бы он был полым - то еще меньше.
Предлагаю свой вариант объяснения:
Масса шарика не 90 миллиграммов, а 900.
Пустотелость шарика не может увеличить его среднюю плотность. Это может быть связано только с пустотелостью черепной коробки:)
-
Не торопитесь язвить про пустотелую черепную коробку. Лучше посчитайте. Не в ту сторону массу откорректировали. Увеличив массу еще на порядок в том же диаметре, вы увеличили плотность еще на порядок, а не уменьшили. Масса шарика 9 мг, а не 900, и не 90.
В реальности, непонятно какая масса и размер, и какой химический состав шарика. С учетом прецизионности опыта, точно можно сказать, что "золото", "шар", масса 90 мг, диаметр 1 мм - четыре эти утверждения между собой ни в каком варианте не бьются, причем расхождение приблизительно на порядок. Мне больше нравится моя идея, что здесь путаница с радиусом/диаметром (это даёт коррекцию в 8 раз и массу неполого шара в 81 мг). Возможно золото было с примесью осмия или платины, тогда могли дотянуть и до почти 90 мг.-
Вы можете развеять свои сомнения обратившись к первоисточнику и включив калькулятор.
Ссылку дал deviant_9 (11.04.2021 18:18):
https://arxiv.org/pdf/2009.09546.pdf
r=(1.07±0.04) mm
Вычисления по средним из этой статьи даст плотность примерно 179.48 г/см3.
Если Вы замените радиус на диаметр, то плотность будет в 8 раз больше, т.е. больше килограмма на кубический сантиметр.
А если признать, что авторы статьи не там поставили точку при записи массы (ошибка на порядок), плотность будет 17.9 г/см3. Это золото примерно 920 пробы.
-
-
Какой конфуз. У этих ученых совсем плохо с учетом драгметалов.
Пусть будет 9 мг золота.
Тогда золотишко разбодяжено - это примерно 900 проба.
https://www.staraya-moneta.ru/lib/1252/
- для сплавов золото, заявленных как 900 проба, показания плотности колбелись от 17,10 г/см3 до 17,24 г/см3.
По справочным данным для сплавов системы золото-медь показание плотности для 900 пробы должно быть не ниже 17,29 г/см3,
Если принять версию о том, что 1 мм это радиус, а не диаметр шарика, то плотность будет в 8 раз меньше 171, 887. Получим 21,486 г/см3. А это уже почти чистый осмий или иридий: https://basetop.ru/samyiy-tyazhelyiy-metall-v-mire-top-10/
Необходимо срочно организовать проверку лаборатории. Если там использовали золото, то его цена почти 100 рублей. А если осмий или иридий, то это примерно 1000 рублей неучтенки.
-
А как же! Уже более 20 лет планируется:
https://www.youtube.com/watch?v=NZF4P8OrcIg
http://adsabs.harvard.edu/abs/1999MeScT..10..514S
Если выяснится, что гравитационная постоянная увеличивается за год на 1.5 * 10-13,
то придется пересматривать основы космологии. А постоянную Хаббла придется разжаловать до локальной характиристики пространства.-
Ого, неслабо. Идея использовать подковообразные орбиты хороша, хотя учет погрешностей наверное непрост... И масштаб эксперимента больше, во всех смыслах. Интересно, масштабируется ли до субмиллиметровых размеров? На первый взгляд - вполне. И есть ли шанс, что полетит? Статья-то древняя...
-
Идея прекрасная. Спутники пастухи, только очень маленькие. Классическая задача о движении трех тел. Даже ничтожное изменение параметров может привести к качественному изменению орбиты.
Если полетит, и будет установлено, что гравитационная постоянная увеличивается, начнется долгожданная "Новая" физика. Снова появится огромное число ссылок на публикацию Эйнштейна 1917 года «Космологические соображения к общей теории относительности».
На первых порах никаких особенных изменений не будет: вместо ускоренного расширения вселенной мейнстримом станет ускоренное сжатие местной группы галактик, заодно с наблюдателями и их приборами. Принцип относительности любого измерения допускает и такое толкование наблюдаемых данных.-
На элементах есть ссылка. А в коментариях рассуждения про лямбда член и планковскую силу.
@
https://elementy.ru/novosti_nauki/432628/Stoletie_OTO_ili_Yubiley_Pervoy_noyabrskoy_revolyutsii?from=rxblock
Столетие ОТО, или Юбилей «Первой ноябрьской революции»
25.11.2015 • Алексей Левин • Физика, История науки • 42 комментария
Это замечание позволяет закончить рассказ о создании ОТО. Уже в 1917 году ее стали применять для конструирования космологических моделей, причем пионером в этом деле опять-таки оказался Эйнштейн: Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie («Вопросы космологии и общая теория относительности»).
https://echo.mpiwg-berlin.mpg.de/ECHOdocuView?url=/permanent/echo/einstein/sitzungsberichte/S250UZ0K/index.meta
Но это уже совсем другая история.
@
-
-
-
https://arxiv.org/abs/2002.11761
А вот и эта статья в арксивном варианте:
https://arxiv.org/abs/2009.09546
Я читал невнимательно, или на самом деле в статье нет ни единого слова про попытки охладить установку для подавления тепловых шумов? И неясно, что же им мешало поднять частоту движения пробной массы, если с их слов это перспективно.
-
"И неясно, что же им мешало поднять частоту движения пробной массы, если с их слов это перспективно".
Я бы построил следующую экспериментальную установку.
Сконструировал бы резонансную механическую систему из описанного ниже сплава, с добротностью колебаний 30000. Например, в виде электромагнитной системы динамиков, катушка которых двигает гофрированную мембрану из этого сплава. Мембрану можно выполнить достаточно жесткой, чтобы ее частота резонанса вместе с первым телом, которое колеблется вперед и назад составляла 12,5 МГц (или другую высокую частоту). Разместил бы одно из тел на некотором расстоянии от привода и соединил с приводом штангой. Сбалансировал бы эту систему, чтобы она сама по себе в среднем не дергалась и экранировал бы все это от электромагнитных помех и поместил в вакуум. Далее вкачал бы в эту систему энергию в пределах одного мегаджоуля или больше. Потом подачу энергию отключил и пока первое тело колеблется, за экранирующей стенкой стал бы наблюдать как эти колебания воздействуют на другое тело, которое взаимодействует с первым.
Является очевидным, что поток энергии через стенку, даже если этот поток не является гравитационными волнами в чистом виде, начнет раскачивать второе тело. При этом мощность потока энергии увеличится пропорционально увеличению частоты в 12 500 000 000 раз больше, чем у описанной в статье установки. Учитывая высокую добротность резонатора относительная полоса пропуская колебаний будет в 5000 раз уже. Также на высокой частоте (например 12,5 МГц) естественные помехи будут ниже. В результате чувствительность установки возрастет более чем 62 500 000 000 000 раз.-
Здесь необходимо иметь ввиду, что система измерения колебаний второго тела, которая показа на рис. 1 не подходит для высокой частоты. В тоже время в качестве приемника колебаний можно использовать второй такой же резонатор со своим пробным телом. Частоты резонаторов должны быть строго одинаковые. Этом случае энергия в виде колебаний в приемном резонаторе будет накапливаться.
Для дополнительного увеличения чувствительности можно в приемном резонаторе организовать активную положительную обратную связь, путем подачи энергии на дополнительную раскачку колебаний резонатора. С помощью этой связи можно скомпенсировать потери энергии в приемном резонаторе, увеличивая его добротность в несколько десятков раз. При этом дополнительно увеличивается чувствительность.-
Следует отметить, что предложенная установка будет практически нечувствительна к различным механическим шумам, в связи с тем, в установке используется сигнал высокой частоты (например 12,5МГц) с очень узкой полосой частот. При этом очень трудно представить другой объект, который расположен на Земле, и который генерируют полностью когерентный сигнал с сигналом в приемным резонаторе, с динамическими напряжениями в материале объекта, приближающихся к механической прочности материала. При этом установка будет нечувствительна к приближению к ней человека или проезду рядом с установкой танка Т90. От электромагнитных помех можно установку хорошо экранировать. В статье отмечается, что значительная часть шумов связана тепловыми шумами торсионного подвеса. Здесь существует такая же проблема. Но эта проблема решается за счет высокой добротности резонаторов. При этом из общего спектра мощности тепловых шумов вырезается очень узкая полоса частот. Что является более эффективным методом подавления шумов по сравнению с просто усреднением шумов как в установке, описанной в обсуждаемой статье. Также резонатор можно охладить до низкой температуры, как предлагал PavelS.
-
Вообще говоря, вот эти посты появилось с связи с комментарием, который написал Юрий Фёдоров. Но подумал, что в этих комментариях содержится не ошибка, и попытался проанализировать ситуацию, исходя из предположения, что высказывания являются правильными. Также немного помог PavelS. В результате получилась экспериментальная установка, которая потенциально лучше по своим параметрам чем установка в обсуждаемой статье. А также появился выход на новый уровень исследований.
-
Длинно, длинно. Но у вас есть ИМХО проблема-неточность - вы полагаете что можно двигать мембрану, но она же даёт "эффект отдачи". Т.е. почему вы думаете что будет колебаться мембрана динамика, а не динамик в целом? Динамик же будет колебаться в противофазе. Т.е. чтобы было переменное грав. поле, которое будет расшатывать пробную массу - нужно 2 массы в генераторе (это не считая третьей-пробной), которые колеблятся в противофазе и на заметном расстоянии одно от другого. У вас же этого нет. Потому про миллионы герц в механике я б забыл, но что мешает поднять частоту хотя бы раз в 10... не ясно.
Да, про охлаждённые кристаллы - вспомнил старые-престарые модели детекторов грав.волн, где нет лазеров, но зато есть подвесной кристалл на тросиках. И там амплитуду не лучиком света детектировали, а туннельным током через узкую щель.
В целом же есть ощущение (именно ощущение неспециалиста!), словно эксперимент поставлен чуть кустарно - вероятно, от него никто звёзд с неба не ждал, потому и вложения не очень.-
Динамик я использовал для простоты изложения. Вы правильно поняли конструкцию. Действительно сам динамик будет двигаться в противофазе.
На самом деле конструкцию лучше сделать, как Вы предлагаете, полностью симметричной для всего резонатора. В качестве резонатора можно использовать конструкцию типа камертона. К одному концу камертона прикрепить компенсирующую массу для равновесия, на на втором конце закрепить первую пробную массу на штанге, с тем чтобы она была на удалении от генератора.
Можно также использовать крутильные колебания, как в электромеханических фильтрах, в которых, собственно, и использовался данный сплав. Только упругий элемент фильтра необходимо сделать большим, чтобы в него можно было вкачать большую мощность.-
Основная идея в данных постах следующая.
1. Существует возможность построить механический резонатор c высокой добротностью с высокой частотой колебаний (по меньшей мере с верхней частотой 500 кГц) и с большой энергией колебаний. Эта задача с инженерной точки зрения является сложной. Но решаемой.
2. За счет очень узкой полосы частот (<10 Гц) для резонатора с частотой 500 кГц можно отфильтровать значительную часть механических и других посторонних шумов. Дополнительно, за счет большой мощности колебаний приводного резонатора обеспечить доминирование этого резонатора над возможными источниками помех.
3. Охладить детали резонаторов до низкой температуры, для исключения собственных тепловых шумов резонаторов.
4. Построить систему из двух резонаторов с использованием пробных тел. Пробные тела закрепить на стержнях (штангах), которые будут выполнять функцию механических волноводов, для того, чтобы удалить резонаторы друг от друга и уменьшить их взаимное влияние и влияние на пробные тела.
Приемный резонатор большим делать не обязательно.
-
-
-
-
-
-
Ссылки на https://journals.aps.org/ доступны для безработных бомжей навроде меня?Есть такая ультимативная весчь: https://sci-hub.do
Подписки от организации (нашего психдиспансера) часто не хватает... Авторы бывают малодоступны (чтобы поклянчить у них напрямую)... А этот Ресурс помогает!.. :)
На мой взгляд обеспечить такую добротность вообще никаких проблем нет. У меня где-то валяются куски сплава и изделия из него, который раньше использовали для электромеханических фильтров. Немного экспериментировал с этим сплавом. Если из него сделать камертон, то он звенит не менее 1 минуты. Делал маятник. Сложилось впечатление, что колебания маятника тормозиться только трением об воздух. При этом реально достижимая добротность оценивалась по меньшей мере в Q = 30000
Я, простите, что-то про периоды и частоты подзабыл.
И на этой почве у меня вопрос: как при периоде в десятки секунд частота получается мегагерцы?
Нет ли тут ошибки? Мнится мне, что частота, - это к-во периодов в одной секунде. Но тогда, если период - десятки секунд, то частота существенно меньше 1 герца (в те самые десятки раз)
Что я тут понимаю неправильно?
И то, что масса земли оказывает такое же воздействие за тридевять земель, как человечье тело в метре тоже шокировало. Рассчеты такие масштабные - это мне не по силам,
но интуитивно кажется, что в такой ситуации в результаты эксперимента планеты солнечной системы должны внести просто ну аффигительный вклад! Ведь их массы вполне себе сопоставимы с массой Земли, а находятся они заметно ближе 5 гпк. Это очень если мягко говорить.
Что в очередной раз я неправильно понимаю?
-
И то, что масса земли оказывает такое же воздействие за тридевять земель
на Землюкак человечье тело в метре
на шарик. Несравнимые между собой вещи.
Сравнение становится ещё более бессмысленным, если вспомнить принцип эквивалентности - по-крайней мере, в отношении далёкой планеты потенциально наблюдаемой является не сама сила её притяжения, а её градиент, то есть приливные силы.
В подписи к рис. 1 указано "подвешены на силиконовой струне", на рисунке подпись - Silica fibre.
Silica - это диоксид кремния, SiO2, в данном случае, видимо, имеется в виду кварцевая нить (как будто более или менее стандартный элемент для подвеса коромысла крутильных установок).
Для контроля английская википедия: Silicon dioxide, also known as silica, is an oxide of silicon with the chemical formula SiO2, most commonly found in nature as quartz... ( https://en.wikipedia.org/wiki/Silica )
Последние новости


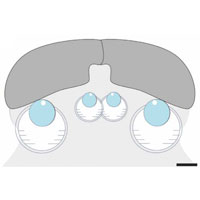

















Рис. 1. Схема эксперимента. Два золотых шарика (ma, mt), закрепленные на жестком коромысле, подвешены на силиконовой струне. Пробная масса ms, находящаяся на среднем расстоянии 2,5 миллиметра от одного из шариков, циклически двигалась с амплитудой 3 мм и периодом около 80 секунд. Между массами располагался экран Фарадея, компенсирующий электростатические силы, а вся установка была помещена в глубокий вакуум на тяжелом оптическом столе. В ходе эксперимента измерялись колебания подвеса по смещению отраженного лазерного луча на фоточувствительном детекторе. Изображение из обсуждаемой статьи в Nature