Что больше?

Иногда бывает, что из постановки вопроса ответ можно легко угадать. Здесь как раз такая ситуация. Про положение отмеченной точки ничего не говорится, а значит, скорее всего, ответ не зависит от того, где именно она находится внутри шестиугольника. Правда, это всё равно нужно обосновывать. Но раз в простом частном случае — когда точка попала в центр шестиугольника — площади красной и зеленой областей равны, то можно надеяться, что они всегда равны, и попытаться доказать уже это.

Стороны правильного шестиугольника равны, поэтому если вспомнить, что площадь треугольника — это половина произведения основания на высоту, то задача сводится к доказательству такого факта: сумма длин высот зеленых треугольников равна сумме длин высот красных треугольников.

Наш шестиугольник двумя способами достраивается до правильного треугольника: можно продлевать основания красных треугольников (получившийся треугольник обозначим Т₁), а можно — зеленых (а этот треугольник назовем Т₂, рис. 1). Получившиеся два треугольника равны друг другу.

Рис. 1.

Заметим теперь, что сумма высот красных треугольников — это сумма расстояний от отмеченной точки до сторон треугольника Т₁. А эта сумма равна высоте данного треугольника. Доказав этот факт, мы получим и решение нашей задачи, потому что по аналогичным соображениям сумма высот зеленых треугольников будет равна высоте треугольника Т₂, а у равных правильных треугольников высоты одинаковые, то есть суммы высот красных и зеленых треугольников равны друг другу.

Итак, докажем, что сумма расстояний от внутренней точки Р правильного треугольника АВС до его сторон не зависит от выбора точки и равна высоте этого треугольника. Для этого соединим эту точку с вершинами треугольника (рис. 2).

Рис. 2.

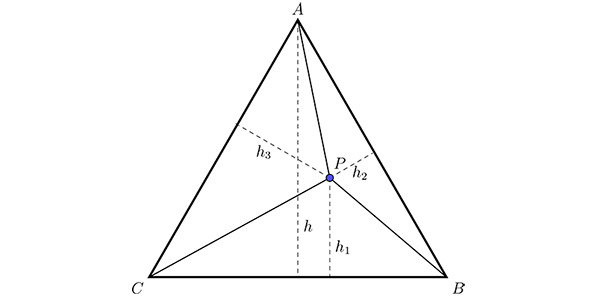
Получается, что треугольник АВС разрезан на три меньших треугольника РАВ, РВС и РАС, а значит, его площадь равна сумме площадей этих трех треугольников:

Применяем все ту же формулу для площади из подсказки и пользуемся тем, что все стороны правильного треугольника равны друг другу (обозначим их длину a):

После сокращений получаем требуемое:

У этой, казалось бы, чисто геометрической задачи есть другое решение, которое, наверное, можно назвать «координатным». Обычно применение метода координат в геометрии ничем хорошим не заканчивается — нужно проделать очень много вычислений и нигде не ошибиться, чтобы получить правильный ответ. Однако иногда бывает, что и в методе координат считать не нужно, если не хочется. Наша задача — хорошая иллюстрация такой ситуации, хотя кому-то она и может показаться немного громоздкой и неуклюжей.

Нам потребуется одно определение и немного дополнительной информации. Функция f(x, y) называется линейной функцией двух переменных, если она имеет вид f(x, y) = ax + by + c, где a, b и c — действительные числа. Графиком такой функции в трехмерном пространстве будет невертикальная (то есть не параллельная вертикальной оси z) плоскость z = ax + by + c. Как известно, плоскость однозначно определяется любой тройкой своих точек, если эти точки не лежат на одной прямой. Это означает, что линейная функция задается своими значениями в трех точках (то же самое другими словами: линейная функция зависит от трех параметров a, b и c, поэтому, чтобы определить эти параметры, нужно знать значения функции в трех точках). В частности, если оказалось, что в трех разных точках (не лежащих на одной прямой) функция принимает одно и то же значение, то она всегда принимает это значение (то есть a = b = 0).

Оказывается, функция расстояния от точки до прямой — линейная. В самом деле, по известной из школы формуле расстояние ρ (на плоскости) от точки с координатами (x₀, y₀) до прямой, заданной уравнением Ax + By + C = 0, вычисляется так:

Эту формулу можно переписать:

Получилась линейная функция в чистом виде.

Раз функция расстояния от точки до фиксированной прямой является линейной функцией (от координат точки), то и площадь треугольника с данным основанием будет линейной функцией от координат противоположной основанию вершины. В самом деле, по все той же формуле площади треугольника из подсказки получается, что площадь — это произведение линейной функции расстояния от точки до прямой (то есть высоты треугольника) на константу (половину длины основания).

Теперь вернемся к задаче. Введем на плоскости нашего шестиугольника систему координат, поместив его центр в начало. Рассмотрим функцию, равную разности между суммарной площадью красных треугольников и суммарной площадью зеленых треугольников. Эта функция — линейная (зависящая от координат отмеченной точки), потому что она получается сложением и вычитанием шести линейных функций. Осталось заметить, что в вершинах и центре шестиугольника эта функция принимает одно и то же значение — она равна 0 в этих семи точках. Значит, эта функция всегда равна 0, то есть сумма красных площадей равна сумме зеленых площадей вне зависимости от положения точки.

Этим же способом можно решить и другие задачи «по геометрии». Например, можно обобщить факт для правильного треугольника, который был доказан в решении: оказывается, что если дан любой правильный многоугольник, то сумма расстояний от внутренней точки до его сторон не зависит от выбора этой точки.

О том, как еще применять такой трюк и похожие рассуждения, в том числе и для гораздо более сложных задач, можно прочитать в статье Д. Звонкина «Эллипс, симметричный как квадрат» (в первом номере журнала «Квант» за 2013 год).