Его прощальный поклон

Игорь Акулич
«Квантик» №4, 2022

Такое название Конан Дойл дал одному из последних рассказов о легендарном сыщике Шерлоке Холмсе. Здесь же речь пойдёт не о вымышленном персонаже, а о реальном человеке, великолепном математике и педагоге, покинувшем нас в 2019 году, — Вячеславе Викторовиче Произволове.

За несколько лет до его кончины я встречался с ним в Москве. Он тогда проживал в районе Митино и сразу же повёл меня прогуляться в расположенный рядом парк с одноимённым названием, рассказывая о встреченных им здесь представителях тамошней фауны — ежах, ужах и т. п.

Но не только живностью оказалось примечательно сие место — всегда можно было подобрать какую-нибудь веточку и найти клочок земли, чтобы представить на обозрение ту или иную красивую задачу, коих Вячеслав Викторович создал, должно быть, неисчислимое количество¹.

Одна из них была придумана довольно давно:

Из одинаковых квадратов составлен прямоугольник². Затем каждый квадрат произвольным образом разрезается диагональю на два равных треугольника. Образуется своеобразная «карта» с треугольными «странами». Требуется доказать, что треугольники можно раскрасить не более чем в три цвета, чтобы любые два треугольника, имеющие общий участок границы, были окрашены в разные цвета.

Ниже изображён пример такого прямоугольника и его раскраски, удовлетворяющей условию (выбраны красный, жёлтый и зелёный цвета):

Для доказательства достаточно указать способ «правильной» раскраски. Будем закрашивать треугольники поочерёдно по строкам сверху вниз, а в каждой строке — слева направо. Тогда каждый очередной закрашиваемый треугольник имеет не более двух уже окрашенных соседей — слева и сверху от себя. Поэтому всегда можно выбрать для него цвет, отличный от цветов этих соседей.

Изложив эту задачу (на мой взгляд, чересчур простую), Вячеслав Викторович спросил:

– А теперь представьте себе, что каждый квадратик, из которых составлен прямоугольник, разбит не диагональю на два равных треугольника, а вертикальным или горизонтальным отрезком на два равных прямоугольника. Всегда ли можно получившуюся карту (состоящую на этот раз из прямоугольных стран) раскрасить в три цвета?

Вопрос заставил почесать голову, причём неоднократно. Не помогло. Наскоро сделанные прикидки с целью найти опровержение тоже ничего не дали.

Пришлось порассуждать. Понятное дело, сразу же вспомнилась знаменитая проблема четырёх красок, утверждающая, что любую карту на плоскости можно окрасить в четыре цвета, чтобы при этом любые две страны, имеющие общий участок границы, были окрашены по-разному³ . Но здесь-то цветов только три!

Возникла робкая надежда, что где-то в литературе или на просторах интернета найдётся, скажем так, частный случай проблемы, доказывающий, что если все страны — равные прямоугольники, то для такой карты хватит и трёх цветов. А вдруг так оно и есть?

Бессильный выдумать что-то получше, я изложил свои соображения.

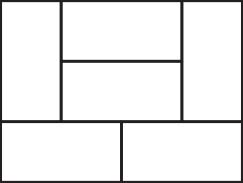
– Неверно! — тут же осадил меня Произволов. — Вот карта из равных прямоугольников, которую нельзя раскрасить в три цвета — четвёртый здесь необходим (рисунок справа).

Поразмыслив, я согласился (а вы согласны?).

– Так каков же ответ? — поинтересовался я.

– Подумайте на досуге! — посоветовал мне Вячеслав Викторович, сдобрив свои слова сочувственной улыбкой. Да, он любил, чтобы собеседники думали сами, и здесь остался верен себе.

Больше нам встретиться было не суждено — общались только по телефону, который как-то не очень подходит для обсуждения задач такого рода (а к переписке по интернету Произволов относился почему-то довольно холодно). Так что правильное решение надолго осталось для меня тайной за семью печатями.

Попытка использовать алгоритм «правильной» раскраски, аналогичный тому, что был применён для карты из треугольников, показала его абсолютную неэффективность. Проявляется она уже для прямоугольных карт малых размеров — см. пример слева.

Если, следуя алгоритму, быстро и бездумно окрасить верхнюю строку в два цвета (что, кстати, представляется вполне естественным и логичным), то ситуация быстро заходит в тупик (рисунок справа). Ведь два горизонтальных прямоугольника, непосредственно соседствующих с красными и жёлтыми, обязаны оба быть зелёными. Но они граничат между собой!

С другой стороны, так и не удалось обнаружить карту, которую нельзя было бы окрасить в три цвета. Каждый раз, используя метод проб и ошибок, удавалось добиться успеха: например, только что рассмотренную карту можно удачно раскрасить, как на рисунке справа.

Видимо, от отчаяния возник «треугольно-прямоугольный» вариант задачи Произволова:

Пусть каждый единичный квадрат, из которых составлен прямоугольник, разбивается произвольным образом либо на два равных треугольника, либо на два равных прямоугольника. Всегда ли можно «правильно» раскрасить такую карту в три цвета?

Но и такой вариант одолеть не удалось. В последующие годы периодически возвращался к задаче, ковырял её со всех сторон — но тщетно. И лишь недавно нашёл эффективный выход: обратиться за посторонней помощью, а именно — в редакцию журнала «Квантик»! Результат превзошёл ожидания: решения обеих задач («прямоугольной» и «треугольно-прямоугольной») были найдены сотрудниками редакции в кратчайшие сроки и оказались они сравнительно несложными. Да, не зря Вячеслав Викторович улыбался на прощание!

Попробуйте докопаться до истины в каждом случае.

Ответы

Решение первой задачи

1. Из одинаковых квадратов составлен прямоугольник. Каждый квадрат произвольным образом разрезали на два равных прямоугольника. Можно ли раскрасить полученную карту, используя только красный, жёлтый и зелёный цвета так, чтобы любые два прямоугольника с общим участком границы были разного цвета?

Вот решение, которое предложил Максим Прасолов. Ответ: раскраска всегда возможна. Опишем, как это сделать. Цвета будем называть сокращённо, по их первым буквам — К, Ж и З соответственно.

Введём понятие «квадрат КЖ». Это означает, что если единичный квадрат разбит на два горизонтальных прямоугольника, то верхний из них — красный, а нижний — жёлтый. Если же он разрезан на два вертикальных прямоугольника, то левый — красный, а правый — жёлтый. Аналогично будем понимать выражения «квадрат ЖЗ» и «квадрат ЗК».

Возьмём теперь произвольный прямоугольник, разбитый на единичные квадраты, и в каждом квадрате укажем схему его окраски (пока не разбивая никакой квадрат на прямоугольники). Эта схема такова (она приведена для прямоугольника 5 × 8, но может быть естественным образом «растянута» на любой прямоугольник иных размеров):

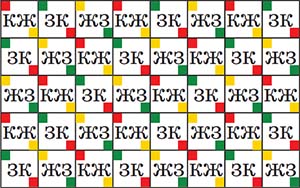
В каждой строке последовательно повторяются тройки квадратов КЖ, ЗК, ЖЗ, после чего снова КЖ и т. п. В столбцах (сверху вниз) — то же самое.

Оказывается, независимо от того, как разрезан каждый квадрат, — по вертикали или горизонтали — итоговая раскраска в три цвета будет «правильной».

Чтобы в этом убедиться, возьмём для начала любой квадрат КЖ. Слева и сверху от него расположены квадраты ЖЗ, а справа и снизу — ЗК (если квадрат КЖ примыкает к  границе, то соседей у него будет меньше четырёх, но от этого хуже не станет). Проверим, что при любых возможных разрезаниях соседей квадрата КЖ все прямоугольники, имеющие общий отрезок границы, будут окрашены в разные цвета.

Для определённости пусть в квадрате КЖ разрез выполнен по горизонтали, вот так:

Рассмотрим соседствующий с ним слева квадрат ЖЗ. Проверим на корректность два варианта его разрезания: по горизонтали и по вертикали. Вот как он «стыкуется» с нашим центральным квадратом (слева — одна возможность, справа — вторая):

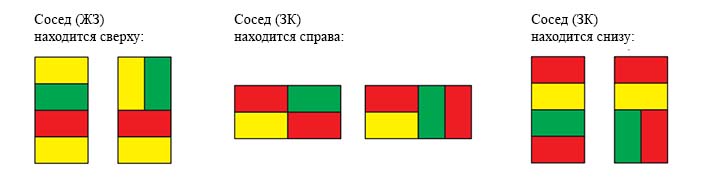
Таким же образом проверяем соседей квадрата КЖ сверху, справа и снизу. Вот что у нас получается.

Как видим, всё в порядке. Но это, правда, только если центральный квадрат КЖ разрезан по горизонтали. А если по вертикали — тоже надо проверять?

Не надо! Ведь строки и столбцы прямоугольника, разбитого на единичные квадратики, совершенно равноправны. Картинка получится точь-в-точь такая же, но отражённая относительно диагонали.

Ладно, с квадратом КЖ разобрались — его соседи ведут себя вполне прилично (с точки зрения соседства по цветам). А квадраты ЖЗ и ЗК? Их тоже нет необходимости проверять, поскольку при «циклической смене цветов» (К на Ж, Ж на З, З на К или наоборот) получатся только что рассмотренные варианты, ибо и цвета тоже равноправны (если сомневаетесь — проверьте).

Итак, тремя цветами всегда можно обойтись.

P.S. А что, если каждый квадратик разбивается вертикальными или горизонтальными отрезками не на два, а на n равных прямоугольников, где n — натуральное число. При каких n получившуюся карту всегда можно «правильно» раскрасить в три цвета?

Случай n = 2 уже рассмотрен. Для n = 1 задача тривиальна — получается обычная клетчатая доска, её можно раскрасить даже в два цвета. А что при n > 2?

Нетрудно сообразить (и потом проверить), что для чётных n такая раскраска возможна, причём для неё можно применить всё тот же алгоритм (только здесь, например, квадрат КЖ означает раскраску нарезанных из него прямоугольников попеременно в красный и жёлтый цвета — слева направо или сверху вниз). Для нечётных же n вопрос остаётся открытым.

Решение второй задачи

2. Из одинаковых квадратов составлен прямоугольник. Каждый квадрат произвольным образом разрезали на две части — либо равные прямоугольники, либо равные треугольники. Можно ли раскрасить полученную карту, используя только красный, жёлтый и зелёный цвета так, чтобы любые две части с общим участком границы были разного цвета?

Вот решение, которое предложил Александр Перепечко. Здесь ответ прямо противоположный: не каждую такую карту удастся правильно раскрасить. Чтобы в этом убедиться, предположим противное и рассмотрим схему разрезания прямоугольника 3 × 3 на рисунке справа (при этом не имеет значения, как разрезан его центральный квадратик, так что мы это и не указываем).

Некоторым из треугольников присвоим номера от 1 до 5, как на рисунке. Пусть треугольник 1 окрашен в какой-то цвет, для определённости — в красный. Тогда примыкающие к нему справа два прямоугольника должны быть жёлтым и зелёным, и потому треугольник 2 — тоже красный. Аналогично, треугольники 3, 4 и 5 — опять-таки красные. Но треугольники 3 и 5 граничат между собой — противоречие.

Художник Алексей Вайнер

¹ Примеры таких задач можно встретить в его же книге «Задачи на вырост», в издательстве МЦНМО как раз выходит новое издание!

² В исходном варианте задачи фигурировал не прямоугольник, а квадрат 10 × 10 (если элементарные квадратики считать единичными), но это, конечно, непринципиально.

³ Впервые проблему четырёх красок чётко сформулировал английский математик Артур Кэли в 1878 году, а доказали её почти через сто лет американцы Кеннет Аппель и Вольфганг Хакен.