Как мы собирали абажур, или Приключения триаконтаэдра (продолжение)
Алексей Панов, Пётр Панов
«Квантик» №8, 2019
Начало см. в «Квантике» № 7, 2019.
Пчелиные соты и заполнение пространства

В своём эссе «О шестиугольных снежинках» Кеплер пишет, что задумался о ромбических многогранниках после наблюдения за пчелиными сотами.
Сотовые ячейки на рисунке 14 обрезаны почти до донышка, которое, как и у кеплеровского додекаэдра, состоит из трёх ромбов. Видно, что слой ячеек периодически, без пробелов, заполняет всю плоскость. На самом деле соты состоят из двух слоёв. Один смотрит на нас, другой расположен сзади и смотрит в противоположную сторону. Если считать, что сотовая ячейка — это половинка ромбического додекаэдра (рис. 14, справа), то каждую из них можно закрыть недостающей половинкой и получить два плотно прилегающих слоя ромбических додекаэдров.

Рис. 14 (слева и в центре). Пчелиные соты с личинками и половинка ромбического додекаэдра. Рис. 15 (справа). Двуслойная конструкция из ромбических додекаэдров, рисунок Михаила Панова
Добавив к этой двуслойной конструкции спереди и сзади ещё по одному слою додекаэдров, потом ещё по одному и так далее, мы заполним всё пространство ромбическими додекаэдрами, получив что-то вроде периодической кристаллической решётки. Наблюдая за сотами, Кеплер нашёл многогранник, которым можно регулярно заполнить пространство!
Кеплеровское эссе «О шестиугольных снежинках» (вышла в 1611 г.) вместе с первыми геометрическими главами Harmonices Mundi справедливо считаются исходной точкой в развитии кристаллографии.
Евграф Степанович Фёдоров (1853–1919)

В 1885 году была опубликована книга Евграфа Степановича Фёдорова «Начала учения о фигурах», положившая начало его знаменитым работам в кристаллографии. В этой книге Фёдоров получил важнейший результат — перечислил все классы многогранников, которыми можно регулярно заполнить пространство. Он назвал их параллелоэдрами.
Характерные примеры — куб, правильная шестиугольная призма, ромбический додекаэдр, удлинённый додекаэдр и усечённый октаэдр. Первые два всем известны, о третьем знал Кеплер. Что касается последних двух, а также точных определений параллелоэдров, отсылаем читателя к статье Н. П. Долбилина «Г. Ф. Вороной и геометрия чисел» и «Калейдоскопу» в «Кванте» № 1 за 2019 г. Нам же важно, что Фёдоров в своей книге обсуждает и вопрос о многогранниках, состоящих из одинаковых ромбов.
Выпуклые многогранники, состоящие из одинаковых ромбов

У нас имеется всё необходимое, чтобы увидеть все такие многогранники, и это мы сейчас сделаем. Напомним только, что выпуклым называют многогранник, у которого нет впадин, то есть его можно приложить к плоской стене любой гранью. Ромбические додекаэдр и триаконтаэдр такими являются (проверьте). Ещё один выпуклый ромбический многогранник был открыт Фёдоровым — это ромбический икосаэдр.
Взглянем на рисунок 4 из прошлого номера, где изображены две чаши и разделяющая их зона, и представим, что эта зона исчезла. Смотрите, чаши идеально подходят друг к другу, нужно только сблизить их и скрепить парные рёбра резинками. Как раз и получится фёдоровский ромбический икосаэдр. Вы легко соберёте его, если у вас есть лишние 20 золотых ромбов с отношением диагоналей 1 : φ.

Рис. 16. Многогранники из золотых ромбов, удаление зон: триаконтаэдр → икосаэдр → додекаэдр → два параллелепипеда
А можно взять готовый триаконтаэдр и удалить из него ту же самую зону, составленную из 10 ромбов, прилегающих друг к другу по параллельным рёбрам. На рисунке 16 сверху изображён триаконтаэдр, а под ним — получающийся после удаления зоны ромбический икосаэдр.
Из этого икосаэдра теперь можно убрать зону, составленную из 8 ромбов, прилегающих друг к другу по параллельным рёбрам, а потом соединить по рёбрам оставшиеся два фрагмента. Получится додекаэдр, изображённый третьим сверху на рисунке 16, и это будет новый многогранник. Он состоит из золотых ромбов, в отличие от кеплеровского додекаэдра, состоящего из ромбов с отношением диагоналей 1 : √2 Сравните их между собой — кеплеровский (рис. 13) намного более симметричен. Некоторые считают, что новый ромбический додекаэдр был открыт математиком Станко Билински в 1960 году, а другие предполагают, что он был обнаружен математиком и картографом Джоном Лоджем Коулом ещё в середине XVIII века.
Наконец, если у додекаэдра Билински удалить зону из 6 ромбов, обязательно получится состоящий из золотых ромбов параллелепипед, но при удалении одних зон он будет сплюснутым, а при удалении других — вытянутым (рис. 16 снизу). На самом деле из любых 6 одинаковых ромбов можно собрать либо сплюснутый, либо вытянутый параллелепипед. Куб — тоже ромбический параллелепипед; при растяжении его вдоль большой диагонали получается вытянутый ромбический параллелепипед, а при сжатии — сплюснутый.
Оказывается, это и есть полный список выпуклых многогранников, состоящих из одинаковых ромбов: триаконтаэдр Кеплера, икосаэдр Фёдорова, додекаэдр Билински, кеплеровский ромбический додекаэдр и ещё целое семейство ромбических параллелепипедов.
Наконец ещё одно, завершающее эту тему упражнение: что получится при удалении различных зон из кеплеровского ромбического додекаэдра (рис. 13)?
Плоские кристаллы, оси симметрии

Рис. 17. Изображение двумерного кристалла графена, полученное электронным микроскопом, размер ячейки составляет доли нанометра
Вернёмся к сотам. Представьте, что вся плоскость заполнена параллелограммами, как на рисунке 8, или шестиугольниками, как на рисунке 14, или квадратиками, как ваша тетрадка по математике. Назовём такой периодический рисунок двумерным кристаллом. Чтобы убедиться в реальном существовании подобных кристаллов, посмотрим на изображение самого известного из них — графена (рис. 17).
Двумерный кристалл можно совмещать сам с собой параллельными переносами разных направлений. Но есть ещё одна возможность — это повороты. Посмотрим на плоский кристалл, составленный из шестиугольных ячеек (рисунок 18, средняя часть), и возьмём прямую, проходящую через центр ячейки и перпендикулярную плоскости рисунка. Тогда кристалл будет самосовмещаться при повороте вокруг этой прямой на 60° = 360°/6. Такую прямую называют осью симметрии кристалла — осью симметрии шестого порядка. Если же на рисунке 18 взять точку, где сходятся три шестиугольные ячейки, и провести через неё перпендикуляр к плоскости рисунка, то самосовмещение будет происходить при повороте вокруг него на 120° = 360°/3 — это ось симметрии третьего порядка.
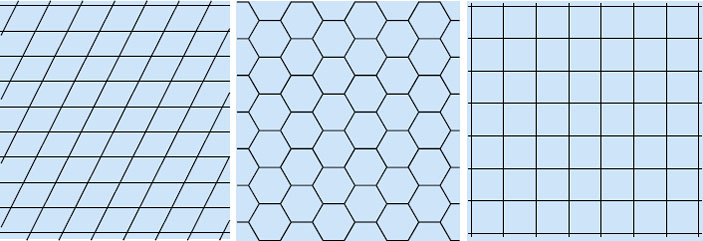
Рис. 18. Двумерные кристаллы
Тут есть над чем подумать. Имеются у этого кристалла оси симметрии других порядков? И то же самое для плоских кристаллов, составленных из параллелограммов и квадратиков (рис. 18, слева и справа): оси симметрии каких порядков у них имеются?
Один из основных законов кристаллографии утверждает, что периодические двумерные и трёхмерные кристаллы могут самосовмещаться только при поворотах на 180°, на 120°, на 90° или на 60°. Другими словами, у них могут быть оси симметрии второго, третьего, четвертого или шестого порядков, но не пятого, седьмого или большего порядка. Кеплер знал об этом, во всяком случае, в Harmonices Mundi у него есть две картинки, ставящие под сомнение существование осей симметрии пятого и седьмого порядков.
Рентгеновская кристаллография
Рентгеновские лучи были открыты в 1895 году. А в 1912 году Максом фон Лауэ, а затем Уильямом Лоуренсом Брэггом и Уильямом Генри Брэггом был создан новый метод исследования кристаллов — метод рентгеновской дифракции, позволяющий увидеть и расшифровать внутреннюю структуру кристалла.

Рис. 19. Принципиальная схема метода Лауэ: пучок рентгеновских лучей рассеивается на кристалле и создаёт дифракционную картину на фотопластинке
В методе, предложенном Лауэ, пучок рентгеновских лучей, направленный на кристалл, взаимодействует с кристаллической решёткой и после рассеяния на ней создаёт на фотопластинке дифракционную картину в виде упорядоченного набора ярких пятен — дифракционных максимумов.
Эти картины зависят от ориентации кристалла и позволяют расшифровать его внутреннее строение, например, установить наличие осей симметрии и их порядок. Если пучок рентгеновских лучей оказался направленным параллельно некоторой оси симметрии кристалла, то дифракционная картина тоже будет иметь ось симметрии соответствующего порядка.

Рис. 20. Один из первых снимков, сделанных по методу Лауэ, — рентгенограмма кристалла цинковой обманки ZnS (1912 год)
При этом для аморфных материалов, типа обычного стекла, дифракционная картина не содержит отдельных пятен, а выглядит размытой.
С рентгеновскими лучами кристаллографы обрели новое зрение, позволившее им заглянуть внутрь кристалла. Фёдоров был восхищён этим открытием. Вот что он пишет по этому поводу своему другу Н. А. Морозову в том же самом 1912 году:
Глубокоуважаемый Николай Александрович. Ваше письмо кончается словами о том, что человеческий глаз никогда не увидит атомов. Вы писали его приблизительно в то время, когда люди увидели атомы собственными глазами, если не сами атомы, то вызванные ими фотографические изображения... Для нас, кристаллографов, это открытие первоклассной важности...
У. Л. Брэгг позже писал о Фёдорове: «Фёдоров был в то время для меня почти легендарной личностью, разработавшей 230 классов кристаллов...».
Итак, в 1912 году физики получили новый замечательный инструмент для исследования кристаллов — начали использовать рентгеновскую дифракцию, а позже ещё и электронную и нейтронную дифракцию.

Слева направо: Макс фон Лауэ, Уильям Лоуренс Брэгг, Уильям Генри Брэгг
Квазикристалл Дана Шехтмана

Дан Шехтман
В 1982 году, ровно через 70 лет после открытия Лауэ, произошло неожиданное событие, в которое сначала никто не верил. Дан Шехтман, изучая кристаллизацию быстро охлаждённого расплава алюминий-марганец, получил следующую дифракционную картину (рис. 21).
Это, конечно же, дифракционная картина кристалла, потому что она состоит из упорядоченного набора дифракционных пиков. И это, конечно же, не может быть дифракционной картиной кристалла, потому что имеет ось симметрии десятого порядка (переходит в себя при повороте на 36° = 360°/10), а это, как мы уже говорили, несовместимо с периодической структурой кристалла.

Рис. 21. Слайд из нобелевской лекции Дана Шехтмана (2011 год)
Шехтман понял, что он совершил невероятное открытие. Однако коллеги не поддержали его, они посоветовали Шехтману успокоиться и ещё раз почитать элементарный учебник кристаллографии. Так что публикация была отложена до 1984 года. Это была первая реакция физиков, но математики оказались более подготовленными к открытию Шехтмана.
Окончание следует.
Художник Анна Горлач





















Рис. 13