Прямое на кривом, или Прогулки по искривлённой поверхности (окончание)

Валерия Сирота
«Квантик» №10, 2020

Окончание. Начало в «Квантике» №8 и №9, 2020.

В прошлом номере мы разобрались, как выглядят «прямые» (точнее, геодезические) линии на цилиндре и на конусе, склеенном из полуплоскости. Однако осталось неясным, как провести геодезическую линию, проходящую через две заданные точки. И сколько таких геодезических? Надеемся, что вы сами справились с этим, но на всякий случай разберём здесь решения двух последних задач.

Решение задачи 6. Есть развёртка конуса с двумя точками A и B на ней. Одну геодезическую, проходящую через А и В, начертить легче лёгкого. Но есть и другая! Ведь можно обходить гору-конус с другой стороны. Это очевидно, например, если обе точки А и В — возле самой линии склейки, по разные стороны от О, и после склеивания окажутся рядом. Но мы сейчас увидим, что это верно для любой пары точек.

Рис. 14

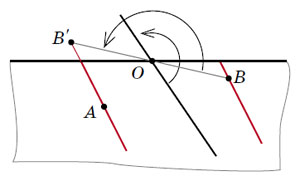
Для этого сделаем «переклейку»! Что если разрезать развёртку нашего будущего конуса по другой образующей — по любой, проходящей между точками А и В? А по старой линии склейки — склеить. Тогда на новой, «переклеенной» развёртке точка B вместе со всем треугольным «отрезанным» сектором окажется повёрнутой вокруг О на угол 180° (рис. 14)¹. Вот через эту симметричную точку B′ и надо проводить прямую.

Теперь можно обойтись и без ножниц и клея, оставаясь на старой развёртке: благодаря идее переклейки мы знаем, куда надо направляться из А, чтобы попасть в В. Поэтому достаточно провести вспомогательную прямую ВО, построить симметричную точку B′, провести из неё в А прямую линию — вот и готова половина нужной геодезической на старой развёртке. Вторую половину легко достроить, как мы делали в задаче 5 из прошлого номера. Даже ещё легче, потому что она пройдёт через точку В, и с лишними углами возиться не нужно...²

Рис. 15

Итак, на нашем конусе через любые две точки, не лежащие на одной образующей, можно провести две «прямые» линии (рис. 15)! То есть всегда есть два «прямых пути» из одного места в другое. При этом, конечно, один из них может быть короче другого. А есть ли ещё прямые пути? Нет, сколько ни переклеивай, новых «прямых» уже не получишь. Проверьте это!

Задача 9. На развёртке конуса задана точка А. Найдите все такие точки В, что оба пути из А в B имеют одинаковую длину.

Теперь пора разобраться с цилиндром.

Рис. 16

Решение задачи 7. Теперь точки А и В даны на развёртке цилиндра. Как провести геодезическую через линию склейки? Можно опять применить «переклейку»: ведь если отрезать нижнюю часть развёртки (например, горизонтальную полосу, включающую одну из точек А и В) и приклеить её сверху — ничего же не испортится? Получится просто другая развёртка того же цилиндра. Точка B при этом переходит в точку B′, которая выше В ровно на ширину развёртки. Значит, если провести прямую АB′, это и будет часть нужной нам геодезической. Теперь можно вернуться к нашей первоначальной развёртке и «достроить» на ней вторую геодезическую (рис. 16). Видно, что обе части геодезической на развёртке параллельны, как и должно быть.

Рис. 17

Нарисуем две развёртки одного и того же цилиндра, одну над другой (рис. 17). При свёртывании их в цилиндр они ложатся одна на другую, точки B и B′ совпадают. Но что если добавить сверху третью развёртку? Линия АB″ — тоже геодезическая! Она «обмоталась» один раз вокруг цилиндра и тоже пришла в точку B (рис. 18). А можно продолжить так и дальше, появятся геодезические, обматывающиеся вокруг цилиндра 2, 3, 5, 10 раз... Их бесконечно много! Да ещё и вниз можно так же «копировать» развёртки, получится ещё одно семейство геодезических, «закрученных» в другую сторону.

Вот это да — на цилиндре через одни и те же точки проходит сколько угодно прямых путей, если, конечно, эти точки на развёртке не попадают на прямую, параллельную линии склейки. Может, и на конусе так же, мы просто что-то не заметили? Нет. Дело в том, что на цилиндре мы использовали симметрию сдвигов — «копировали» развёртки вверх, и у точки В получилось бесконечно много изображений. На конусе симметрия — поворот вокруг точки О; можно тоже сделать две развёртки, накладывающиеся друг на друга, — верхняя и нижняя полуплоскости. Но только две! Второй поворот вокруг точки О на 180° вернёт точку В обратно, новых её изображений и новых путей к ней не возникнет.

Более того: если сделать конус пошире, то есть брать для развёртки не полуплоскость, а сектор больше 180°, то и двух путей может не получиться: на рисунке 19 точки А и В соединяют две геодезические (красная и синяя), а точки А и С или A и D — только одна (соответственно, жёлтая и зелёная). В первом случае нет пути через линию разреза, во втором — нет другого пути, кроме как через разрез. На пологом холме для достаточно близких точек уже нет прямого пути «в обход холма». Обратите внимание — на таком конусе концы любой геодезической уже не параллельны, а расходятся.

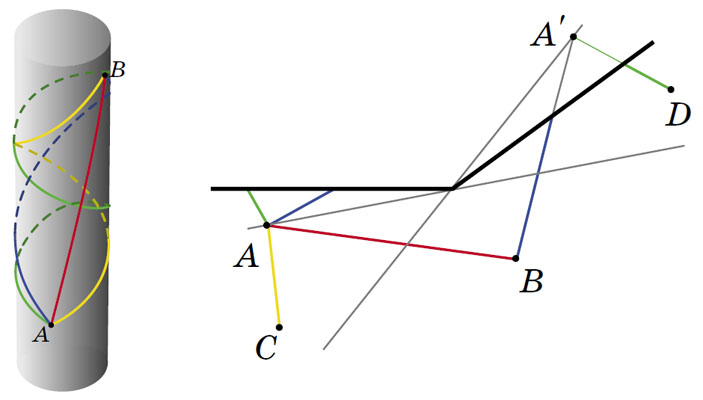
Рис. 18 (слева) и 19

Узкие конусы

Рис. 20

А теперь давайте сделаем конус поуже. То есть для развёртки возьмём не целую полуплоскость, а сектор поменьше. Поскольку про переклейку всё остаётся в силе, все геодезические по-прежнему будут выглядеть одинаково и зависеть только от одного параметра — минимального расстояния до вершины конуса. Поэтому достаточно рассмотреть какую-то одну геодезическую; возьмём такую, которая на нашей развёртке перпендикулярна линии склейки (рис. 20). Раз она подходит к склейке под прямым углом, то и уходить от неё должна тоже под прямым..., и смотрите, что получается — эта «прямая» линия пересекается сама с собой! На склеенном конусе получается «галстучек» (рис. 21)

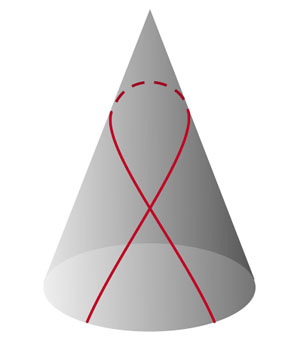
Рис. 21

А дальше ещё веселее. Если взять ещё более узкий конус, с развёрткой меньше 90°, то — глядите! — после этого самопересечения обе части геодезической снова пересекают линию склейки, причём в одном и том же месте! Обратите внимание, что из-за симметрии картинки на развёртке всё выглядит так, как будто геодезическая отражается от линии склейки. На самом деле это не отражение, хоть и очень на него похоже — концы геодезической при переходе линии склейки меняются местами. Как только вы сложите развёртку в конус — это сразу станет видно.

Это уже второе пересечение геодезической самой с собой. А может быть ещё и третье — если после этого пересечения линии склейки концы геодезической снова пересекутся в середине развёртки... Если конус совсем узкий, геодезическая обвивает его много раз, на каждом обороте пересекаясь сама с собой два раза — под самой верхней (ближней к вершине) точкой и строго по другую сторону от этой точки (рис. 22).

Рис. 22

Задача 10. У каких конусов, то есть при каких углах развёртки, геодезическая пересекается сама с собой один раз? Два раза? Три раза? Четыре раза? N раз?³

Вот мы и узнали, как выглядят геодезические даже на самых крутых и высоких горах. Отважным путешественникам, впрочем, ещё есть чем заняться — хорошо бы разобраться, как же там ходить из одной заданной точки в другую.

Задача 11. Найдите (начертите на развёртке) все геодезические, проходящие через заданные точки А и В, для конуса с углом развёртки а) 120°; б) 90°; в) (для самых смелых) 110°.

Задача 12. На конусах с какими углами развёртки выполнено свойство: через любые две точки проходят не меньше трёх геодезических? А не меньше чем n геодезических? (Пары точек, лежащие на одной образующей, не рассматриваем.)

Вот и подходит к концу наше путешествие по отвесным цилиндрам и крутым конусам⁴. Представьте теперь, в заключение, что вы находитесь в горной стране из высоких-превысоких гор и крутых ущелий. Если в таком месте пойти прямо, по геодезической — вы, скорее всего, рано или поздно попадёте на склон горы и, поскольку это конус, вынуждены будете карабкаться по нему по спирали вверх, а потом вниз, как на рисунке на полях. Спустившись, вы продолжите движение уже не в том же направлении, что раньше, а в какую-то другую сторону... Отсюда видно, что идти прямо, напролом в горах не только опасно, но и глупо: если даже все поверхности гладкие и нигде нет ни трещин, ни крутых обрывов, и вы не сломаете шеи по дороге — вы всё равно придёте неизвестно куда. Вот почему для горных туристов и альпинистов так важны ум и опыт.

Художник Алексей Вайнер

Ответы

9. Все точки на луче, выходящем из О и перпендикулярном ОА, — красный луч на рисунке.

10. 90° ≤ x < 180°; 60° ≤ x < 90°; ... ; \( \frac{180°}{N + 1} ≤ x < \frac{180°}{N} \).

11. а) При угле развёртки 120° всю плоскость можно поделить на три развёртки, накладывающиеся одна на другую при сворачивании в конус. У точки B есть ещё два «изображения» на других развёртках, которые совмещаются с ней при наложении. Поэтому и геодезических — три; выходя из А, можно целиться в любую из трёх B, и придёшь куда нужно.

б) Тут на плоскости помещается 4 развёртки, значит, и путей в любую точку — тоже 4. Зелёная и красная геодезические по дороге из А в В делают полный оборот вокруг вершины.

в) Всё почти так же, как для 120°, но теперь три развёртки не полностью заполняют плоскость — остаётся зазор в виде сектора шириной 30°. При построении каждого пути приходится думать, где этот зазор рисовать — чтобы ваши прямые линии проходили только по развёрткам и не пересекали зазор. Опасность возникает, если точка А или В близка к границам развёртки: например, пусть B близка к верхней границе, как на рисунке. Построим изображение B₁: вторую развёртку приклеиваем к верхней границе нашей, первой — теперь, если точка А на рисунке лежит левее красной линии (вариант А₁), рисуем зелёную геодезическую, направляя её в B₁. (А третью развёртку приклеиваем к правой нашей границе.) Если же А правее красной линии (А₂), то линия А₂B₁ прошла бы через зазор. Поэтому верхнюю (вторую) развёртку нужно приклеить не к нашей верхней грани, а вплотную к третьей развёртке, оставляя зазор слева, между первой и второй развёртками. Тогда при свёртывании цилиндра совпадёт с B уже не B₁, а B₂ — целимся в неё и рисуем синюю геодезическую. Для некоторых точек А можно построить оба изображения — и «синее», и «зелёное». Догадайтесь, где находятся эти точки. Ещё два изображения (от I и III секторов) получаются легко.

12. \( x ≤ \frac{360°}{n} \). Число геодезических определяется числом развёрток, помещающихся на плоскости, и, соответственно, числом «изображений» каждой точки.

¹ Можно резать прямо по той образующей, на которой лежит точка В. Тогда после переклейки она окажется на границе.

² А можно для второй половины подумать про другую переклейку — и построить точку А′, симметричную точке А...

³ Подсказка. Не бойтесь этой задачи, она совсем не страшная. Нужно просто спокойно порисовать развёртки и геодезические на них. Единственное, что нужно знать из геометрии, — это что сумма углов любого треугольника на плоскости равна 180°.

⁴ Цилиндры и конусы удобны тем, что для них можно сделать плоскую развёртку. Существует много других «развертывающихся поверхностей», но среди всех поверхностей в пространстве они составляют крайне малую часть. Остальные поверхности — сферы (мячики), торы (бублики) и другие — нельзя склеить из кусков плоскости. Строить на них геодезические сложнее. Но принцип — идти «маленькими шажками» — всегда тот же.