Почтовое занятие

Игорь Акулич
«Квантик» №6, 2020

— Сегодняшнее занятие математического кружка назовём почтовым. Конечно, можно было бы придумать что-нибудь более торжественное, например «Эйлерово» или «Кэрроллово», но дело не в названии. Для начала посмотрите на эти две картинки (рис. 1).

Рис. 1

Они имеют вполне почтовые имена — «закрытый конверт» (слева) и «открытый конверт» (справа). Сумеете ли вы нарисовать каждую из этих фигур, не отрывая карандаша от бумаги и не проводя дважды одну и ту же линию? Задача очень известная...

— Да, нам её задавали! Закрытый конверт изобразить нельзя, а открытый — можно.

— Правильно. Причём при рисовании открытого конверта начинать надо непременно от одного из нижних углов, а заканчивать — в другом нижнем углу, иначе вы обречены на неудачу. А закрытый конверт откуда ни начинай рисовать — ничего не выйдет.

— А почему?

— Сейчас поговорим об этом. Началось всё с легендарной истории, которую можно прочесть чуть ли не в каждой книге по истории математики. Шёл XVIII век. Великий учёный Леонард Эйлер, проживавший тогда в Кёнигсберге, задался вопросом: можно ли обойти все семь имевшихся в нём мостов (соединявших острова в дельте реки), пройдя по каждому только один раз? Эйлер поступил очень остроумно: «стянул» острова, соединявшие мосты, в точки, а сами мосты «растянул» в линии (которые, кстати, не обязаны быть прямолинейными!). И получилась вот такая фигура (рис. 2), задача же свелась к тому, чтобы выяснить, можно ли её нарисовать, соблюдая те же требования (будем называть их «эйлеровыми»), что и для наших конвертов.

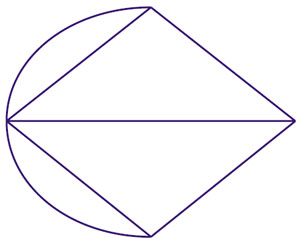
Рис. 2

Эйлер доказал, что нельзя, но самое главное — разработал простые правила, позволяющие по внешнему виду любой подобной фигуры определить, можно её нарисовать или нет. Во-первых, фигура, которую можно изобразить, должна быть связной, то есть не состоящей из отдельных кусков (это очевидно). Далее необходимо рассмотреть так называемые узлы — точки, в которых сходятся несколько линий или же от которых отходит ровно одна линия («свободный конец»). Например, у закрытого конверта пять узлов — четыре угла и центр, а у открытого... вообще-то тоже пять.

— Как это пять? А верхний угол?

— Ну, формально можно считать его узлом, в котором сходятся две линии. Но тогда с тем же успехом можно считать узлом и вообще любую точку на любой линии. Поэтому принято точки на линиях узлами не считать, то есть не рассматривать узлы, к которым подходят две линии. Впрочем, это не имеет значения, поскольку итоговый ответ от наличия таких узлов не зависит.

— А от чего он зависит?

— Сейчас скажу. Разделим узлы на два типа: чётные и нечётные — в зависимости от того, сколько линий сходится в узле. Если одна, три, пять и т.д. — узел нечётный, а если четыре, шесть, восемь... — то чётный.

Пусть мы нарисовали какую-либо фигуру по указанным правилам. Рассмотрим любой промежуточный узел, то есть узел, где маршрут не начинается и не заканчивается. При рисовании карандаш сколько-то раз «входит» в этот узел и столько же раз «выходит» из него. А значит, промежуточный узел — непременно чётный! Поэтому если у фигуры больше двух нечётных узлов, её изобразить нельзя — ведь не более двух из них могут быть крайними, и обязательно найдётся промежуточный нечётный узел, что недопустимо.

Несколько сложнее доказать, что если у связной фигуры нечётных узлов ровно два или вовсе нет, то фигуру нарисовать можно (попробуйте это сделать!). При этом если нечётных узлов нет, то начинать рисовать можно с любой точки, и закончится процесс в той же самой точке, а если нечётных узлов два, то начинать нужно непременно с одного из них (а закончится путь в другом).

— А если нечётный узел один?

— Я ждал этого вопроса. Кто скажет, какова судьба фигуры, содержащей ровно один нечётный узел?

— Пусть он сначала покажет такую фигуру!

— Очень точное замечание. Потому что таких фигур не бывает. Кто может доказать?

— Я! Допустим, что фигура с одним нечётным узлом всё-таки существует. Подсчитаем для каждого узла количество отходящих от него линий и сложим все эти числа. Получится сумма одного нечётного числа и нескольких чётных. Ясно, что эта сумма будет нечётной. Но поскольку каждая линия соединяет два узла, эта же сумма равна удвоенному количеству линий и обязана быть чётной. Противоречие!

— Верно. Итак, фигур с единственным нечётным узлом быть не может, как, впрочем, и фигур с любым нечётным количеством нечётных узлов.

Основываясь на результатах Эйлера, мы видим, что закрытый конверт имеет четыре нечётных узла (в углах), вследствие чего его изобразить невозможно, а открытый — только два, так что его нарисовать удастся, однако начать придётся с одного из этих узлов. В «мостовой» же схеме Кёнигсберга все 4 узла — нечётные, то есть ответ для неё отрицательный.

Рис. 3

А теперь перенесёмся в XIX век — следующий после Эйлера — когда лучший математик среди писателей и лучший писатель среди математиков, несравненный и загадочный Льюис Кэрролл предложил задачу: нарисовать по правилам Эйлера фигуру на рисунке 3.

Вооруженные нашими знаниями, мы без труда определим, что нарисовать такую фигуру можно, но Кэрролл кое-что усложнил — дополнительно потребовал, чтобы в процессе рисования никакие линии не пересекались (кстати, эта задача встречалась и в «Квантике»). Его собственное решение весьма остроумно: он закрасил некоторые части, на которые делят плоскость проведённые линии, после чего чуть-чуть «срезал углы» (рис. 4). Осталось просто обвести контур закрашенной фигуры — и готово!

Рис. 4

И возникает естественный вопрос: каким условиям должна удовлетворять фигура, чтобы её можно было нарисовать «по правилам Кэрролла» — то есть без пересечения линий? Понятно, что требования Эйлера должны быть соблюдены. Но, может быть, этого мало и есть ещё ограничения? Подумайте.

...Пауза...

— Похоже, ничего в голову не приходит. Тогда возьмите «из головы» несколько фигур, которые можно нарисовать «по Эйлеру», и попытайтесь сделать для них то же «по Кэрроллу». Получится или нет? Начните хотя бы... с открытого конверта! Ну как?

— Есть! Получилось!

— И не удивительно. Оказывается, справедлива следующая теорема (кстати, совсем не очевидная): если фигуру можно нарисовать по правилам Эйлера, то её же всегда можно нарисовать и по правилам Кэрролла. Какие будут мысли насчёт доказательства?

— А если использовать раскраску, как Кэрролл?

— Идея, конечно, заманчивая. Но мы попробуем рассуждать по-другому. Итак, пусть у нас имеется фигура из линий и узлов, которую можно нарисовать «по Эйлеру». Понятно, что при её рисовании возможные пересечения линий могут быть только в узлах — и не просто в узлах, а только если сходящихся линий в узле не меньше четырёх. Возьмём любое такое пересечение. Пронумеруем линии, образующие пересечение, в том порядке, в котором мы их проходим при рисовании (рис. 5, а). Будем рисовать по-другому: с первой линии пойдём на третью, затем обходим участок старого маршрута карандаша в обратном направлении, приходим во вторую линию и сворачиваем на четвёртую, далее как раньше (рис. 5, б). Как изменилось количество пересечений?

Рис. 5

— Уменьшилось на один!

— Не торопитесь. Да, одно пересечение мы устранили. Но в узле может сходиться больше четырёх линий, и тогда карандаш ещё сколько-то раз проходит через узел. Если, например, он подошёл к узлу из угла между линиями 1 и 4 и вышел в угол между линиями 2 и 3, как на рисунке 6 обозначено красным, то число пересечений уменьшится ещё на два.

Рис. 6

— А если карандаш по-другому прошёл через узел?

— В других случаях все пересечения сохранятся, а новых не добавится. Случаев мало, на рисунке 6 указаны все, не считая аналогичных. В результате число пересечений уменьшилось на 1 и ещё на 2 для каждого красного прохода карандаша, поэтому, продолжив изменять маршрут, мы устраним все пересечения.

Итак, если фигуру можно нарисовать «по Эйлеру», то и по «Кэрроллу» тоже можно! Вижу, всех радует это открытие, кроме... вон того молодого человека с унылым видом. В чём ваше горе?

— Я нашёл фигуру ровно с одним нечётным узлом!

— Очень любопытно. Покажите.

— Показать могу только кусочек, и могу ещё дать общее описание. Вот посмотрите.

— Что это... А! Понятно! Можете успокоиться, противоречия нет: тут законы чётности неприменимы. Так что всего хорошего, занятие закончено.

Вопрос к читателям. Какую (хоть примерно) фигуру мог найти «строптивый» кружковец?

Ответ

Почему ученик не смог нарисовать всю схему целиком? А что если она... бесконечная! Вот пример. Возьмём линии, делящие бесконечную плоскость на клетки. Все узлы (вершины клеток) будут чётными, поскольку в каждом сходятся 4 линии. А теперь удалим один из лучей, идущий вверх из какого-то узла. Фрагмент получившейся фигуры показан на рисунке. У неё ровно один узел нечётный (в нём сходятся три линии), а остальные — чётные.

Никакого противоречия нет — в доказательстве мы подсчитывали, сколько линий суммарно выходит из всех узлов, но если сумма бесконечна, то говорить о её чётности не имеет смысла.

Художник Алексей Вайнер