Химическая краса — углеродная коса

М. Ю. Корнилов
доктор химических наук
«Химия и жизнь» №6, 2007

Наверное, каждый человек от мала до велика умеет заплетать косу из трех прядей волос или веревок. На рисунке показана коса из конопляных канатов: ее ширина — три сантиметра, толщина — один.

Косы, как и узлы и некоторые другие изделия из нитей и полос бумаги, служат объектами математических исследований с точки зрения их топологии — геометрической структуры, которая не меняется при непрерывной деформации, в частности при растягивании или выворачивании наизнанку. Например, правая и левая перчатки, как и любой другой предмет и его зеркальное изображение, имеют одинаковую топологию, а кольцо и узел, два отдельных кольца и кольца, соединенные подобно звеньям цепи, — разную.

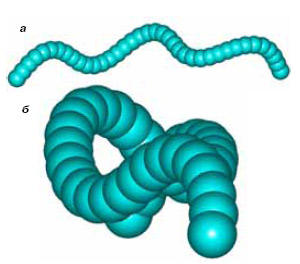
А вот углеродные косы из карбиновых нитей, то есть нитевидных молекул углерода, — это нечто новое по своим масштабам, хотя топология их не нова. О таких химических косах пойдет далее речь. На следующем рисунке мы видим модель простейшей косы, сплетенной с помощью «химического конструктора» из трех карбиновых нитей.

Модель простейшей косы, сплетенной с помощью «химического конструктора» из трех карбиновых нитей (изображение: «Химия и жизнь»)

Изображены три ортогональные (взаимно перпендикулярные) проекции карбиновой косы (ширина 0,7 нм, высота 0,4 нм): вид сверху (а), сбоку (б), с торца (в).

Для сравнения еще на одном рисунке показаны ортогональные проекции шнурка из трех карбиновых нитей (диаметр шнурка 0,4 нм).

Ортогональные проекции шнурка из трех карбиновых нитей (изображение: «Химия и жизнь»)

Сравнение последних двух рисунков позволяет видеть, чем существенно отличается коса от шнурка, в котором нити скручены, а не переплетены. У шнурка проекции а и б тождественны, а у косы они разные. Это отличие проявляется особенно наглядно, если косу и шнурок свернуть в кольцо. На рисунках показаны: а — карбиновое кольцо С₁₀₀₈ в форме шайбы (Ш) и обруча (О) диаметром 10,8 нм; б — кольцо-шнурок С₈₂₈ , его диаметр 8,5 нм.

а — карбиновое кольцо С₁₀₀₈ в форме шайбы (Ш) и обруча (О); б — кольцо-шнурок С₈₂₈ (изображение: «Химия и жизнь»)

Для косы возможны два геометрически разных, хотя и топологически одинаковых случая. Если сворачивать кольцо в одной плоскости, получается структура, напоминающая шайбу, а если в другой — обруч. На первом рисунке показаны проекции кольца-шайбы и кольца-обруча сверху и сбоку, а на втором — то же для кольца из карбинового шнурка.

Как были построены такие кольца? Каждое из них собирали из 12 одинаковых линейных фрагментов, ориентированных в плоскости под углами 30^о друг к другу и затем соединенных между собой. Для правильной стыковки фрагментов косы и последующей оптимизации ее геометрии необходимо, чтобы в кольце было целое число «волн» каждой карбиновой нити. В случае шнурка это требование значения не имеет.

Ортогональные проекции фрагмента обруча: вид сбоку (а) и с торца (б) (изображение: «Химия и жизнь»)

У читателя, знакомого со стереохимией, может возникнуть вопрос: хиральны ли углеродные косы и кольца из них? Как и любая пространственная спираль, шнурок, составленный из однонаправленных спиральных нитей, всегда хирален. Может показаться, что и кольца-косы, построенные из закрученных карбиновых нитей, которые, как синусоида, извиваются в плоскости кольца и к тому же виляют в перпендикулярном направлении, также должны быть хиральными. На следующем рисунке показаны ортогональные проекции фрагмента обруча: вид сбоку (а) и с торца (б).

Тем не менее сравнение каждой такой нити и всего кольца в целом с их зеркальными отражениями дает парадоксальный результат: у кольца-обруча они тождественны, а у его «геометрического изомера» — кольца-шайбы — разные! Таким образом, структура (Ш) хиральная, а (О) — нет. Путем «выворачивания наизнанку» структуру (Ш) можно перевести в соответствующий энантиомер, который будет ее зеркальным изображением. При этом на промежуточном этапе образуется ахиральная структура (О) — полная аналогия с энантиомерными молекулами и плоским, ахиральным переходным состоянием. Что касается линейной косы, то она ахиральна только тогда, когда состоит, как и кольцо, из целого числа «волн» или имеет бесконечную длину.

Заплетание модели карбиновой косы оказалось делом непростым. Карбиновые нити, стремящиеся в идеале быть линейными, всячески противятся изгибанию, при оптимизации геометрии распрямляются и выскальзывают из зацеплений. Решение проблемы было найдено в результате анализа устройства косы, заплетенной из канатов: она состоит из повторяющихся волнообразных фрагментов. Ниже показаны этапы сборки и оптимизации геометрии косы из трех карбиновых нитей (в каждой паре рисунков верхний — вид сверху, нижний — вид сбоку): (а) две плоские полуокружности из 12 атомов углерода; (б) зигзагообразная цепь из 16 полуокружностей; (в) скелет косы из трех сложенных цепей до оптимизации геометрии; (г) «одетая» коса до оптимизации и (д) после оптимизации геометрии (незакрепленные концы разошлись).

Этапы сборки и оптимизации геометрии косы из трех карбиновых нитей (изображение: «Химия и жизнь»)

На первом этапе делаем такой фрагмент из карбинового 12-угольника, который оптимизируем, затем разрываем одну из связей и поворачиваем одну половину на 180° относительно противоположной связи (рис. а). Далее составляем зигзагообразную цепь из таких фрагментов (рис. б), добавляем к ней две такие же копии и размещает их на равных расстояниях вдоль направления цепи (рис. в). Это уже коса, хотя еще «сырая». В ней карбиновые нити заплетены как нужно и нигде не пересекаются (рис. г), но имеют угловатую структуру. При оптимизации геометрии модель косы быстро приобретает округлые формы. Концы, если они не закреплены, начинают распрямляться и расходиться (рис. д).

Закрепление концов кос с помощью вспомогательных фрагментов (изображение: «Химия и жизнь»)

Закрепить концы косы можно вспомогательными фрагментами. Этот способ напоминает известный прием: чтобы косы не расплетались, их перехватывают резиновыми колечками или завязывают ленточками.

Косы из трех, четырех и пяти карбиновых нитей (изображение: «Химия и жизнь»)

Описанный прием позволяет собрать косы, а из них кольца из любого числа нитей. Правило моделирования здесь такое: число полуокружностей, из которых делается первоначальный 12-атомный фрагмент косы (рис. а), должно быть на единицу меньше числа карбиновых нитей (так, для косы из трех нитей было взято две полуокружности, из четырех нитей — три полуокружности и т. д.). Далее показаны косы из трех, четырех и пяти карбиновых нитей. Для наглядности одна из нитей другого цвета. Справа показаны косы с торца.

Подобным образом из карбиновых нитей можно изготовить широкую косу — коврик. На рисунке показаны: (а) заготовка и отдельная нить карбинового коврика, (б) — то же после оптимизации геометрии; (в) фрагмент оптимизированного коврика.

а — Заготовка и отдельная нить карбинового коврика, б — то же после оптимизации геометрии; в — фрагмент оптимизированного коврика (изображение: «Химия и жизнь»)

Форма каждой нити заготовки коврика, как и в случае косы, имеет вид волнистой линии (рис. а). Чтобы нити не распрямлялись, их концы попарно соединяют по контуру. После оптимизации геометрии коврика прямоугольная сетка плоских нитей превращается в сетку трехмерных спиралей (рис. б, в). Кольца из карбинового шнурка оказываются нестабильными. При оптимизации геометрии они постепенно деформируются, утрачивают круглую форму и превращаются в спутанный клубок, который напоминает «фараоновы змеи».

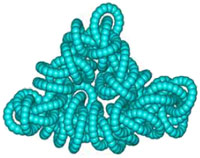
На этом рисунке показан результат оптимизации геометрии нестабилизированного шнурка из трех карбиновых нитей. Подобным же образом ведут себя кольцевые спирали из нанотрубок (см. «Химию и жизнь», 2005, № 9).

У колец из кос такого не происходит: переплетенные, а не скрученные карбиновые нити стабилизируют друг друга. Для стабилизации кольца из шнурка достаточно вставить вдоль его оси еще одно карбиновое кольцо.

На рисунке показана стабилизация кольца С₈₂₈, сделанного из шнурка, соосным кольцом С₂₀₈ из одной незакрученной карбиновой нити. Такой «комплекс» оптимизируется, образуя кольца правильной формы.

Описанным ранее методом косу удается завязать в узел. Вот на следующем рисунке показан узел-трилистник С₁₀₀₈ из карбиновой косы — топологический изомер карбиновых колец. Математики называют такую фигуру «клеверным листом» и обозначают как 3₁.

Кольца можно соединить в катенаны или другие переплетения.

Тройной катенан (а): каждое кольцо С₁₀₀₈ продето через два других. Вторая структура (б) отличается от предыдущей способом соединения колец (изображение: «Химия и жизнь»)

Топология таких «комплексов» отличается от топологии отдельно взятых колец. Вначале показан тройной катенан: каждое кольцо С₁₀₀₈ продето через два других. Если разорвать любое кольцо, два других остаются соединенными. Вторая структура отличается от предыдущей способом соединения: те же самые кольца соединены так, что все три держатся вместе. Достаточно убрать любое из них — два оставшихся будут просто лежать друг на друге.

Можно сплести модель кольца из одной-единственной карбиновой нити.

На последнем рисунке показано кольцо С₃₁₅₀ из косы, заплетенной из одной карбиновой нити (диаметр кольца (б) 22,2 нм). В увеличенном виде показано, как выглядит коса по разные стороны от плоскости (а, в) и с торца кольца (г). Подобное плетение образует нить в швейных, сапожных и некоторых производственных машинах, у которых нет челнока. Предлагаем читателю решить, хиральны структуры трилистника и кольца из карбиновой нити или нет.

Кольцо С₃₁₅₀ из косы, заплетенной из одной карбиновой нити (диаметр кольца (б) 22,2 нм). В увеличенном виде показано, как выглядит коса по разные стороны от плоскости (а, в) и с торца кольца (г) (изображение: «Химия и жизнь»)

Таким образом, нити карбина могут быть уникальным материалом для «ткацких» изделий молекулярного уровня. Дело за современными Жаккарами и Зингерами, изобретателями ткацкого наностанка и швейной наномашинки.

Молекулярные шнурки более сложного, чем у карбина, строения известны давно, их заплетает ее величество Природа — это спиральные макромолекулы амилозы, ДНК и т. д. Не исключено, что и косы уже существуют в природе на молекулярном уровне, если не в виде колец, узлов или катенанов, то, по крайней мере, в незамкнутом виде. Но они пока еще не попали в поле зрения ученых и ждут своего звездного часа.