Задачка для фермера

Ясно, что если из какого-то места на поле видно пугало, то пугало «видит» это место — препятствий и укрытий по условию нет. В пункте 1 сначала подумайте, приблизительно какую область «видит» одно пугало в зависимости от своего положения на каждом из полей. После этого уже несложно понять, сколько пугал достаточно, чтобы «покрыть» все поле.

Третье поле имеет более хитрую конфигурацию, чем первые два. В этом случае может помочь еще вот какое соображение. У каждого участка забора есть «внутренняя» сторона — та, которая смотрит на поле. И из каждой точки этой стороны должно быть видно какое-нибудь пугало. Ясно, что это пугало находится в той полуплоскости относительно прямой, содержащей данный участок забора, с которой к нему прилегает поле.

Пункт 2 гораздо сложнее, ведь там неизвестна форма поля, а известно только лишь число сторон у забора. Придумайте поля, для которых нельзя обойтись менее чем 1, 2, 3 и 4 пугалами. Есть ли поле, для которого и 4 пугал недостаточно?

1. Ясно, что на первом поле одного пугала не хватит. А про два пугала легко понять, как их расположить, чтобы все поле просматривалось. Например, так, как на рисунке 1 (пугала обозначены красными кружочками).

Рис. 1.

Теперь разберемся с кольцеобразным полем. Одно пугало «видит» область, которая показана слева на рисунке 2. Форма этой области зависит от положения пугала на поле, но устроена она всегда одинаково: видно все, что лежит «снаружи» от угла образованного касательными к внутренней границе поля, а также участок между этими касательными и ближней частью внутреннего забора. Заметим, что если в этой области не будет других пугал, то на поле обязательно останутся непросматриваемые участки. Это ясно из центральной картинки на рисунке 2: маленький зеленый участок не виден ни из красного, ни из синего пугала. Даже если второе пугало будет стоять очень близко границе области видимости первого, то такой «треугольничек» все равно останется, только он будет совсем маленьким. Нас это не устраивает. Значит, если поле имеет форму кольца, то каждое пугало должно «видеть» хотя бы еще одно. А на самом деле даже два — по одному со стороны каждой из касательных. То есть меньше чем тремя пугалами не обойтись. В нашем случае трёх и хватит (рис. 2, справа). Но если отношение радиуса внутреннего круга к радиусу внешнего будет ближе к 1, то, возможно, придется использовать больше пугал.

Рис. 2.

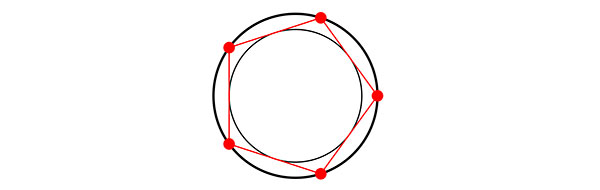
На рисунке 3 показан случай, когда меньше пяти пугал не закроют все поле. Кстати, интересное упражнение: найти зависимость числа пугал от отношения радиусов окружностей.

Рис. 3.

Переходим к третьему полю. Из подсказки следует, что одного пугала точно не хватит: в каждой из двух закрашенных полуплоскостей должно быть по пугалу (рисунок 4, слева). А вот двумя обойтись можно. Пример подходящего расположения показан на рисунке 4, справа.

Рис. 4.

2. Из подсказки следует, что есть примеры, в которых минимальное число пугал равно 1, 2, 3 и 4. Они изображены на рисунке 5.

Рис. 5.

А вот доказательство того, что вне зависимости от формы 12-угольника понадобится не больше четырех пугал, уже не очень тривиально. В этом частном случае можно провести разумный перебор. Но оказывается, что верна общая теорема:
Если поле имеет форму многоугольника с N сторонами, то фермеру понадобится не более N/3 пугал.

Её мы обсудим в послесловии.

Прежде чем доказывать теорему, убедимся, что оценку из неё нельзя улучшить, то есть что при любом N существует поле в форме N-угольника, на котором нельзя расставить меньше пугал. Имеется в виду, что при N = 3m потребуется ровно N/3 = m пугал. При N = 3m + 1 или N = 3m + 2 ближайшим целым числом к N/3, которое меньше него, тоже будет m, и именно столько пугал придется использовать. На рисунке 6 показано, как строить примеры для таких N. В каждом зеленом участке должно стоять пугало, а всего таких участков как раз m.

Рис. 6.

Эту теорему можно доказывать по-разному, но мы обсудим самое короткое и изящное из доказательств, которое принадлежит Стиву Фиску. В этом доказательстве ярко проявляется «единство» науки, когда идеи из разных областей математики оказываются применимы в неожиданных ситуациях. Наша задача кажется геометрической, и первый её пункт относится исключительно к геометрии. Во втором пункте ставится более общий вопрос, который можно отнести к геометрической комбинаторике. А вот доказывать теорему мы будем при помощи графов.

Итак, начнем с того, что проведем N – 3 непересекающиеся диагонали, которые разобьют многоугольник на треугольники. Такое разбиение называется триангуляцией. При этом один и тот же многоугольник можно триангулировать разными способами, но нам не важно, как именно это делать — подойдет любой. Пример триангуляции изображен на рисунке 7.

Рис. 7.

Теперь посмотрим на многоугольник как на граф, вершинами которого будут вершины многоугольника, а ребрами — стороны и проведенные нами диагонали. Оказывается, вершины этого графа можно раскрасить в три цвета (пусть это будут красный, желтый и зеленый) так, чтобы каждое ребро соединяло вершины разных цветов. Проще всего доказать это индукцией по числу вершин графа. Если вершин всего три, то всё очевидно. Пусть их N и по предположению индукции мы умеем правильно раскрашивать любые графы с меньшим числом вершин. Возьмем любой треугольник. У него есть сторона, которая является диагональю многоугольника. Покрасим её концы в два разных цвета. Эта сторона делит граф на два меньших триангулированных графа, которые мы сможем правильно покрасить, причем с учетом уже покрашенных двух вершин. Это и дает окраску всего графа.

Итак, вершины нашего графа окрашены. Сосчитаем, сколько вершин каждого цвета. Ясно, что одно из этих трех чисел не превосходит двух других. Пусть это число вершин красного цвета, тогда их явно не больше N/3. Осталось поставить в каждую из этих вершин по пугалу. Поскольку в каждом треугольнике есть красная вершина, то каждый из них, а значит, и всё поле будут под присмотром. Что и требовалось.

Здесь, честно говоря, был замят вопрос о том, почему всегда можно построить триангуляцию многоугольника. Это действительно верно. Желающие могут попробовать доказать это самостоятельно или посмотреть доказательство в замечательной книжке М. Айгнера и Г. Циглера «Доказательства из Книги», по мотивам одной из глав которой написана эта статья. Название книги — отсылка к словам Пауля Эрдёша. Он любил говорить, что есть Книга, в которую Бог заносит совершенные доказательства теорем. При этом он уточнял, что математик не обязан верить в Бога, а вот в Книгу он верить должен.

Также рекомендую зайти на страницу Art gallery problem — там описаны некоторые интересные обобщения этой задачи.