Многогранник в кубе
Задача
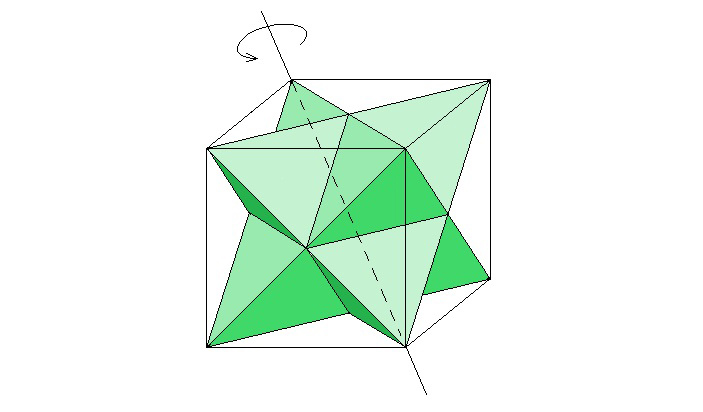
В куб вписаны два правильных тетраэдра, объединением которых является звездчатый многогранник (рис. 1). Куб вместе с этим многогранником вращается вокруг одной из своих диагоналей. При этом образуются два тела вращения: одно — от вращения куба, другое — от вращения звездчатого многогранника. Найдите отношение объемов этих двух тел вращения.
Подсказка
Попробуйте отдельно рассмотреть тело, получающие при вращении куба, и отдельно тело, получающееся при вращении звездчатого многогранника. Определите их форму, чтобы правильно вычислить объем.
Решение
Найдем вначале объем тела, полученного при вращении куба \(ABCDA_1B_1C_1D_1\) вокруг его диагонали \(AC_1\). Форма фигуры вращения определяется трехзвенными ломаными с концами в вершинах \(A\) и \(C_1\), например, \(ADD_1C_1\) или \(AA_1D_1C_1\).

Рис. 2.
Звено \(AD\) имеет с осью вращения общую точку \(A\), поэтому при вращении это звено определяет боковую поверхность конуса. Высота \(AF\) конуса равна трети диагонали \(AC_1\), радиусом основания конуса является перпендикуляр \(DF\), опущенный из вершины \(D\) на ось вращения \(AC_1\).
Если ребро куба равно \(a\), то \(AF=\frac{a\sqrt3}{3}\), \(DF=\frac{a\sqrt3}{3}\), поэтому объем конуса равен \(V_1=\frac13\cdot\left(\frac{a\sqrt{6}}{3}\right)^2\cdot\frac{a\sqrt3}{3}=\frac{2}{27}a^3\sqrt{3}\).
Звено \(C_1D_1\) определяет при вращении точно такой же конус, значит, его объем \(V_2\) тоже равен \(V_2=\frac{2}{27}a^3\sqrt{3}\).
Прямая, содержащая ребро \(A_1D_1\) по отношению к оси \(AC_1\) вращения является скрещивающей прямой. При вращении такая прямая задает однополостный гиперболоид вращения.
Покажем это в общем виде для скрещивающихся прямых \(a\) и \(l\), где \(l\) — ось вращения (рис. 3). Взаимное расположение скрещивающихся прямых \(a\) и \(l\) определяется расстоянием \(d=ON\) и углом \(\alpha=\angle MNK\) между этими прямыми. Введем прямоугольную систему координат \(\mathrm{O}xyz\) таким образом, чтобы ось \(\mathrm{O}y\) совпадала с прямой \(l\), ось \(\mathrm{O}z\) — с прямой \(ON\). Плоскость \(\mathrm{O}xy\) можно считать одной из плоскостей сечения полученной при вращении фигуры. Произвольная точка \(M(x,\ y,\ z)\) прямой \(a\) при вращении будет оставлять следы-точки \(M_1\) и \(M_2\) на секущей плоскости \(\mathrm{O}xy\), и в координатной плоскости \(\mathrm{O}xy\) будут иметь координаты \(M_1(x,\ y)\) и \(M_2(-x,\ y)\).

Рис. 3.
Найдем уравнение линии, по которой секущая плоскость пересекает фигуру вращения. В прямоугольном треугольнике \(MNK\) катет \(MK=x\mathrm{tg}\,\alpha\), тогда в прямоугольном треугольнике \(MM_0K\) гипотенуза \(MM_0^2=y^2\mathrm{tg}^2\,\alpha+d^2\). Учитывая, что \(MM_0=MM_1=x\), получим уравнение искомой линии \(x^2-y^2\mathrm{tg}^2\,\alpha=d^2\). Это уравнение легко преобразовывается к виду \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\) задает гиперболу с полуосями \(a\) и \(b\), а поверхность, которая получается вращением гиперболы вокруг ее оси симметрии \(\mathrm{O}y\), является однополостным гиперболоидом вращения.
Вернемся к вращению куба вокруг его диагонали. Как уже говорилось, полученная при этом фигура вращения представляет собой объединение двух равных конусов и фигуры, похожей на цилиндр с криволинейной образующей. Теперь-то мы знаем, что эта дуга гиперболы, полученная вращением ребра \(ВС\). Для куба со стороной \(a\) вышеуказанные параметры уравнения принимают значения \(d=\frac{a\sqrt{2}}{2}\), \(\mathrm{tg}\,\alpha=\sqrt{2}\), поэтому уравнение гиперболы получается таким: \(x^2-2y^2=\frac{a^2}{2}\).

Рис. 4.
Объем однополостного гиперболоида вычислим с помощью интеграла. Боковая поверхность гиперболоида определяется дугой \(MN\) гиперболы. При этом ординаты точек \(K\) и \(F\) равны \(\pm\frac{a\sqrt{3}}{6}\), поэтому получим:
\[V_{\mathrm{г}}=2\pi\int\limits_{0}^{\frac{a\sqrt{3}}{6}}x^2\;\mathrm{d}y=2\pi\int\limits_{0}^{\frac{a\sqrt{3}}{6}}\left(2y^2+\frac{a^2}{2}\right)\;\mathrm{d}y=\frac{5\pi a^3\sqrt{3}}{27}.\]
Рис. 5.
Остается просуммировать объемы двух конусов и одного гиперболоида и вычислить объем фигуры, полученной при вращении куба:
\[V=2\cdot\frac{2}{27}a^3\sqrt{3}+\frac{5\pi a^3\sqrt{3}}{27}=\frac{\pi a^3\sqrt{3}}{3}.\]С этой частью задачи разобрались.
Тело вращения звездчатого многогранника получается при одновременном вращение двух тетраэдров (рис. 6). При вращении тетраэдра получается конус, высотой которого является отрезок \(C_1F=\frac{2a\sqrt{3}}{3}\), равный 2/3 диагонали \(AC_1\) куба, а радиусом основания конуса является отрезок \(DF=\frac{a\sqrt{6}}{3}\), поэтому объем одного (зеленого) конуса равен \(V=\frac13\pi\left(\frac{a\sqrt{6}}{3}\right)^2\cdot\frac{2a\sqrt{3}}{3} =\frac{4}{27}\pi a^3\sqrt{3}\).

Рис. 6.
Рассмотрим последовательность конусов \(K_1\), \(K_2\), \(K_3\) и \(K_4\) с высотами \(C_1L\), \(C_1K\), \(C_1P\) и \(C_1P\), которые относятся друг к другу как 1:2:3:4 соответственно. Конусы подобны, поэтому их объемы выражаются так: \(V_1=\frac{1}{64}V\), \(V_2=\frac{8}{64}V\), \(V_3=\frac{27}{64}V\), \(V_4=V\).
Зная эти соотношения, легко вычислить объем тела, полученного при вращении двух конусов (зеленого и желтого):
\[2(V_2+(V_4-V_3))=\frac{45}{32}V.\]С учетом того, что \(V=\frac{4}{27}\pi a^3\sqrt{3}\), находим объем тела, полученного при вращении двух конусов: \(V=\frac{5}{24}\pi a^3\sqrt{3}\).

Рис. 7.
Теперь можно найти искомое отношение:
\[\left(\frac{5}{24}\pi a^3\sqrt{3}\right) : \left(\frac{1}{3}\pi a^3\sqrt{3}\right)=\frac58.\]Послесловие
Тела вращения, объемы которых мы вычисляли в решении (рис. 7), вполне можно считать волчками. Если, например, напечатать фигуру такой формы на 3d-принтере и быстро раскрутить волчок вокруг его оси (коей является диагональ куба), то он некоторое время будет устойчиво вращаться, потому что его движение подчиняется закону сохранения момента импульса. Но со временем из-за трения угловая скорость вращения уменьшается, а когда она становится маленькой, ось волчка начинает отклоняться от вертикали и прецессировать, в итоге волчок совсем замедляется и падает.
Изучением законов вращения волчка занимались многие ученые. Еще в XVIII веке Леонард Эйлер сформулировал задачу о движении твердого тела вокруг неподвижной точки. Он сам решил один из ее частных случаев, другой частный случай разобрал французский математик и механик Жозеф Луи Лагранж.
Важный вклад в решение задачи внесла Софья Ковалевская, первая в мире женщина-профессор математики. В 1888 году она стала лауреатом премии Парижской академии наук за решение третьего классического случая задачи о вращении твердого тела вокруг неподвижной точки. Несмотря на достигнутые успехи (в том числе важный вклад в исследование механики движения волчка внесли российские математики Г. Г. Аппельрот, Б. К. Млодзиевский, Н. Е. Жуковский, А. М. Ляпунов и Н. Б. Делоне), полного решения задачи о вращении волчка в общем виде до сих пор нет — волчок не хочет раскрывать все свои секреты.
Почему вообще столько ученых тратили свои силы на решение задачи, поставленной Эйлером? Дело в том, что вращение волчка имеет большой практически смысл: волчок является основным элементом гироскопа — прибора, используемого для контроля ориентации в пространстве. Невозможно представить без гироскопов современную навигацию в авиации, в морских судах, в космосе. Да и сами планеты являются, по сути, большими волчками — значит, у них с волчками общие законы движения.
В одном из тренировочных тестов для подготовки к ЕГЭ по математике я встретил простой, на первый взгляд, вопрос: какая фигура получится при вращении куба вокруг его диагонали? В качестве возможных вариантов предлагались четыре фигуры вращения (рис. 8). Ученику в ответе достаточно было указать только номер фигуры. Попробуйте проверить свое пространственное мышление и выбрать нужную фигуру. Впрочем, вы уже знаете ответ.

Рис. 8.
Правильный ответ можно отыскать экспериментально. Для этого из обычного кубика сделаем игрушку, каждому знакомую с детства — юлу. В деревянном кубике просверлим отверстие вдоль диагонали куба и плотно вставим в него какую-либо спицу подходящего диаметра. Результат показан слева на рис. 9. Запустив этот импровизированный волчок, узнаем ответ (точнее, подтвердим наши рассуждения из решения).

Рис. 9.
Конечно, на ЕГЭ не до экспериментов. Правильный ответ школьник может найти, если вспомнит, что при вращении одной из скрещивающихся прямых вокруг другой, образуется криволинейная поверхность. Читатели же могут посмотреть видео на замечательном сайте «Математические этюды», в котором очень наглядно показан процесс образования этого тела вращения.
Отметим также, что объем средней части этого тела, являющейся однополостным гиперболоидом вращения, в решении задачи вычислен с помощью определенного интеграла. При этом пришлось устанавливать вид и уравнение кривой, от вращения которой образуется этот гиперболоид. Но можно поступить иначе, и воспользоваться формулой Симпсона для вычисления объемов: \(V=\frac{h}{6}(S_0+4S_{\mathrm{ср}}+S_1)\), где \(h\) — высота тела, \(S_0\) и \(S_1\) — площади верхнего и нижнего оснований, \(S_{\mathrm{ср}}\) — площадь «среднего» сечения, которое параллельно основаниям и равноудалено от них. Для нашего гиперболоида \(h=\frac{a\sqrt3}{3}\), основаниями тела являются круги радиуса \(\frac{a\sqrt6}{3}\), поэтому \(S_0=S_1=\frac{2\pi a^2}{3}\), а серединным сечением тела является круг радиуса \(\frac{a\sqrt2}{2}\), поэтому его площадь равна \(S_{\mathrm{ср}}=\frac{\pi a^2}{2}\). По формуле Симпсона получим \(V=\frac{a\sqrt{3}}{18}\left(\frac{2\pi a^2}{3}+4\cdot\frac{\pi a^2}{2}+\frac{2\pi a^2}{3}\right)=\frac{5\pi a^3}{27}\), то есть то же самое значение. Вообще, формула Симпсона предназначена для приближенного вычисления объемов, но в этом случае формула дает точное значение объема, потому что площадь горизонтального сечения гиперболоида вращения является квадратичной формой.
Второй волчок получается при вращении звездчатого многогранника. Как мы уже выяснили, с одной стороны, этот звездчатый многогранник является объединением двух тетраэдров (рис. 10).

Рис. 10.
С другой стороны, он получается присоединением восьми правильных тетраэдров ко всем граням желтого октаэдра (рис. 11).

Рис. 11.
Этот известный в математике многогранник называют звездчатым октаэдром. Иоганн Кеплер по-латыни называл его stella octangula (восьмиконечная звезда). Его можно считать трехмерным аналогом гексаграммы.
Последние задачи















Рис. 1.