Умножение и домино

Начать можно с того, чтобы нарисовать шаблон, состоящий из соответствующего количеству костяшек четного числа клеток. Рисуя шаблоны в разных пунктах, нужно следить, чтобы клетки шаблона можно было объединить в пары в форме прямоугольников 1×2 (то есть костяшек домино). При заполнении клеток не должны появляться цифры 7, 8 и 9, которых нет в домино.

а) Этот пункт — самая простая часть задачи. Решений возможно несколько, на рис. 2 показано одно из них: \(351\times403=141453\).

Рис. 2.

б) Для этого пункта тоже было найдено несколько решений. Вот одно из них, предложенное Виктором Корсуковым: умножение чисел 2506 и 14056 записано столбиком с помощью 18 костяшек.

Рис. 3.

в) Поскольку требуется найти пример на умножение с наименьшим числом костяшек, по начать поиск надо с умножения двузначных чисел.

В зависимости от количества знаков в промежуточных произведениях возможны четыре варианта:
    1) оба промежуточных произведения двузначные;
    2) первое промежуточное произведение двузначное, второе — трехзначное;
    3) первое промежуточное произведение трехзначное, второе — двузначное;
    4) оба промежуточных произведения трехзначные.

На рис. 4 показаны соответствующие шаблоны.

Рис. 4.

Все эти варианты не реализуются. Действительно, в первых двух вариантах в шаблонах получается нечетное число квадратиков. В последних двух вариантах раскрасим шаблон в шахматном порядке и увидим, что число черных квадратиков не равно числу белых. А поскольку каждая костяшка домино всегда покрывает один белый и один черный квадратик, то и эти два шаблона при помощи домино записать невозможно. Нужно отметить, что в третьем варианте теоретически возможен перенос разряда при сложении промежуточных произведений — тогда итоговое произведение будет четырехзначным. Но в этом случае общее число квадратиков станет нечетным.

Значит, нужно увеличить число разрядов в сомножителях. Рассмотрим умножение двузначного числа на трехзначное. Логично считать, что цифра в разряде десятков трехзначного числа равна 0. В зависимости от количества знаков в промежуточных произведениях снова получается четыре возможности:
    1) оба промежуточных произведения двузначные;
    2) первое промежуточное произведение двузначное, второе — трехзначное;
    3) первое промежуточное произведение трехзначное, второе — двузначное;
    4) оба промежуточных произведения трехзначные.

Соответствующие шаблоны приведены на рис. 5.

Рис. 5.

Легко видеть, что первые два из этих случаев не реализуются: в них нечетное число квадратиков. В третьем варианте общее число квадратиков четное (их 14), а «шахматный тест» не «запрещает» представить его при помощи 7 доминошек. Четвертый вариант тоже подходит по обоим этим признакам, но для него требуется 8 костяшек. Значит, надо сначала попробовать подобрать конкретные числа для третьего варианта. Подходящий пример показан на рис. 6: \(31\times204=6324\).

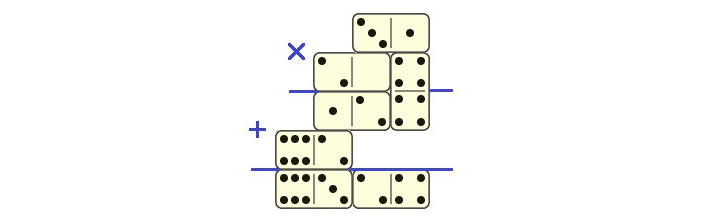
Рис. 6.

Как появилась эта задача? У нее достаточно длинная история. Пример на умножение, записанный с помощью домино, я впервые увидел в книге «Математическая смекалка» известного популяризатора математики Б. А. Кордемского в следующей задаче:

Рис. 7.

При помощи четырех костей домино изобразили умножение трехзначного числа 551 на однозначное число 4. Попробуйте разместить все 28 костей домино так, чтобы получилось 7 «умножений», подобных показанному на рисунке. Шесть «умножений» вы построите без особого труда. А вот над седьмым придется подумать. Все же это возможно.

Все так и оказалось — «последний бой, он трудный самый»! Решая эту задачу, я каждый раз «тормозился» на седьмом умножении. А когда справился с ней, то увлекся идеей Кордемского и придумал свой вариант умножения чисел, записанный с помощью костяшек домино, в котором появилось дополнительное требование: каждый множитель должен содержать хотя бы две ненулевые цифры. На рис. 2 приведен первый — придуманный мной еще в 1987 году — пример «доминошного» умножения, записанный с помощью 10 костяшек.

Тогда же на страницах районной газеты «Заря» я организовал конкурс «Головоломка» по решению занимательных задач. Конкурс продолжался несколько лет. Конечно, я не упустил случая включить задачу «Умножение в домино» в один из туров конкурса, — с надеждой, что участники конкурса найдут пример с большим (чем 10) числом костяшек. Задача вызвала большой интерес у участников, редакция получила много ответов на задачу, а лучшим было решение школьника Виктора Гулякина, содержащее 15 костяшек (рис. 8).

Рис. 8.

Имея несколько разных решений, я в 1991 году опубликовал одно из них с 12 костяшками домино (то самое с рис. 1) в журнале «Наука и жизнь» с предложением читателям найти другой пример на умножение многозначных чисел, в котором используется больше костяшек домино. Читатель Юрий Гусаков придумал пример, содержащий 17 костяшек (рис. 9). На мой взгляд, это уникальное решение, которое и по сей день является рекордом, — как пример с наибольшим числом костяшек домино, найденный вручную, без помощи компьютера. Именно поэтому в нашей задаче предлагалось найти решение с 18 костяшками — чтобы «превзойти» рекорд Гусакова.

Рис. 9.

Затем почти на 20 лет задача попала в забвение — не было никаких продвижений в сторону увеличения числа костяшек в примере на умножение. Поиск новых решений связан с перебором большого количества вариантов, а человеческие возможности тут сильно ограничены по сравнению с компьютерными. Конечно, хотелось получить пример, записанный всеми 28 костяшками полного набора домино. Поэтому я обратился к программистам Константину Шамсутдинову и Тальмону Сильверу с просьбой найти такой пример. Ответ оказался неожиданным: примера с 28 костяшками не существует. Компьютерный поиск, проведенный ими независимо друг от друга, показал, что максимально возможное число костяшек в примере на умножение равно 25. Каждый из них прислал свой пример, записанный при помощи 25 костяшек (рис. 10).

Рис. 10.

А вот и список всех примеров с 25 костяшками: 32556651×14200, 341632556×1000040, 2320651063×20005, 3402144522×10003, 4312405261×10005, 5031413566×10004, 5330254156×10400, 5345022114×10003, 5435022114×10003, 6246424033×5050, 6421042633×10005, 6632555615×2040. Всего их 12 штук. Таким образом, задача по поиску примеров, записанных с наибольшим количеством костяшек домино, решена. Решающую роль в этом сыграло применение компьютера.

Графически изображать их нет смысла, потому, что при желании можно перемножить числа каждой пары и восстановить границы всех домино, участвующих в записи конкретного примера. Отметим, что в этом случае не работает переместительное свойство умножения — переставлять множители нельзя. Нельзя не потому, что получится другое произведение, а потому что после перестановки множителей в промежуточных произведениях могут появиться цифры больше 6, а также может возникнуть ситуация, когда клетки шаблона невозможно будет разбить на пары в форме прямоугольника 1×2.