Разные размерности
Что такое размерность фигуры, то есть, грубо говоря, сколько нужно параметров, чтобы точно задать положение любой точки в этой фигуре, — вопрос отнюдь не простой, хотя интуитивно может и казаться понятным, что это такое. Математики, естественно, размышляли над ним и придумали несколько разных определений, которые в некоторых случаях могут даже давать разные численные результаты применительно к одной и той же фигуре. Это, как ни странно, вовсе не означает, что в математике что-то не так, а, наоборот, позволяет при помощи разных подходов изучать разные объекты.
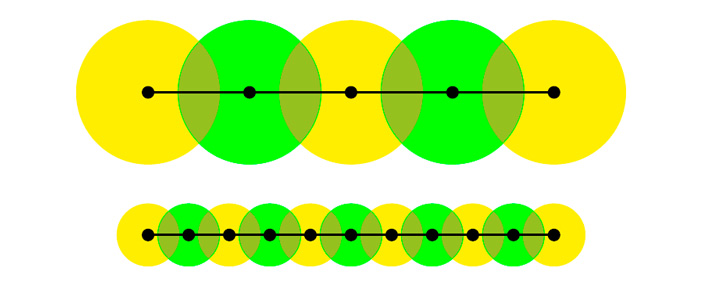
Классическое определение звучит следующим образом: (топологической) размерностью (или размерностью Лебега) фигуры F называется наименьшее целое число n, обладающее тем свойством, что при любом ε > 0 существует конечный набор шаров радиуса не больше ε, покрывающих фигуру F так, что любая точка из F принадлежит не более чем (n + 1) шару. Предполагается, что шары не содержат свою границу; для плоских фигур вместо шаров можно взять круги. Например, отрезок является одномерной фигурой, потому что его можно покрыть кругами так, как показано на рис. 1: каждая точка содержится не более, чем в двух различных кругах, причем это свойство не зависит от их размера, то есть можно указать покрытие кругами любого меньшего (сколь угодно малого) размера, обладающее тем же самым свойством. Контрольный вопрос: чему равна топологическая размерность окружности?
Однако описанный выше способ — не единственный подход к определению размерности. Говорят, что фигура F имеет фрактальную размерность d, если при разбиении ее на кусочки, каждый из которых в k раз меньше исходной фигуры, оказывается, что общее число кусочков равно kd. Например, отрезок является одномерной фигурой, потому что если разбить отрезок длины 1 на отрезочки длины 1/3, то общее количество таких отрезочков будет 31 = 3, а если на отрезочки длины 1/10, то 101 = 10 (и так далее для любого числа отрезочков). Точно так же, квадрат — фигура двумерная, ведь если разбить квадрат со стороной 1 на квадратики со стороной 1/3, то общее количество таких квадратиков будет 32 = 9, а если на квадратики со стороной 1/10, то 102 = 100 (и так далее).
Для большинства привычных фигур топологическая и фрактальная размерности совпадают (то есть n = d). Однако для некоторых фигур это оказывается не так: тогда как топологическая размерность всегда является целым числом, их фрактальная размерность получается дробной. Типичный пример таких фигур — собственно, фракталы.
Задача
Рассмотрим довольно известный фрактал ковер Серпинского. Он строится итеративно следующим образом. В качестве начального объекта берется квадрат. На первом шаге нужно мысленно разбить этот квадрат на 9 одинаковых квадратов, а затем (уже не мысленно, а вполне реально) удалить центральный из них. Затем, на втором шаге, каждый из оставшихся восьми квадратов также надо мысленно разделить на 9 квадратиков, после чего удалить центральный (рис. 2). На третьем шаге мы проводим ту же самую операцию с каждым из 64 оставшихся квадратиков и так далее. То, что останется в итоге после завершения этой бесконечной процедуры (то есть точки, которые принадлежат всем получающимся в процессе фигурам) и называется ковром Серпинского.
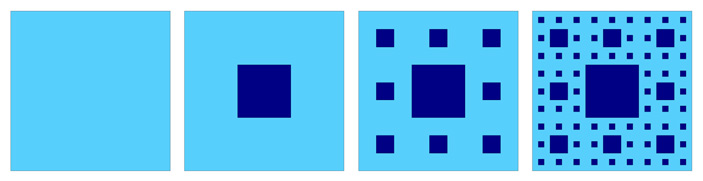
Рис. 2. Первые шаги построения ковра Серпинского
а) Покажите, что топологическая размерность квадрата (с внутренностью) равна 2.
б) Проверьте, что топологическая размерность ковра Серпинского равна 1. Чему равна его фрактальная размерность?
Подсказка 1
В пункте а) достаточно проверить следующие два утверждения:
1) Можно покрыть квадрат кругами любого наперед заданного радиуса так, чтобы, во-первых, каждая точка квадрата принадлежала хотя бы одному кругу, а во-вторых, каждая точка квадрата принадлежала не более чем 3 кругам одновременно.
2) В первом утверждении нельзя заменить 3 круга на 2 (этим проверяется, что размерность квадрата случайно не окажется равной 1).
Подсказка 2

Рис. 3.
Чтобы построить покрытие, удовлетворяющее условиям первого утверждения из подсказки 1, расположите центры кругов в вершинах треугольной решетки. Какими должны быть радиусы кругов (по отношению к расстоянию между их центрами)?
Чтобы убедиться в справедливости второго утверждения из подсказки 1, рассмотрите два пересекающихся круга (рис. 3). Можно ли нарисовать еще один круг так, чтобы ему принадлежала точка A, но не принадлежала ни одна точка из пересечения данных двух кругов (напомним, что границы кругов самим кругам не принадлежат)?
Подсказка 3
В пункте б) будем считать, что длина стороны квадрата, который служит основой для ковра Серпинского, равна 1. Рассмотрим фигуру, получающуюся на втором шаге итеративного построения ковра Серпинского (квадрат, из которого вырезано 9 квадратов). Покажите, что эту фигуру можно покрыть кругами радиуса \({\sqrt2}/{6}\) так, чтобы каждая ее точка попала не более, чем в два круга. Как теперь построить покрытие ковра Серпинского кругами сколь угодно малого радиуса?
Решение
а) Чтобы ответить на вопросы из второй подсказки, рассмотрим сначала равносторонний треугольник со стороной 1. Поместим в его вершины маленькие круги и начнем их медленно раздувать. Проследим за качественным поведением картинки, отметив ключевые моменты, когда ее свойства принципиальным образом меняются. Сначала, когда радиусы кругов небольшие, они находятся относительно далеко друг от друга и не пересекаются. В первый раз ситуация меняется в тот момент, когда радиус достигает значения \({1}/{2}\), — круги касаются друг друга. Как только радиус превышает это критическое значение, возникают области попарного пересечения кругов, однако внутри треугольника по-прежнему существует непокрытая кругами область и нет точки, принадлежащей всем трем кругам одновременно. Второй раз ситуация меняется, когда радиус достигает значения \({\sqrt3}/{3}\) — в этот момент все три окружности проходят через одну точку (центр треугольника). После прохождения этой критической отметки возникает область, покрытая всеми тремя кругами одновременно, а весь треугольник оказывается накрыт кругами полностью (рис. 4).

Рис. 4.
Отметим также, что если мы приставим друг к другу два одинаковых равносторонних треугольника и поместим два равных круга в противоположные вершины, то эти круги не будут пересекаться друг с другом, если их радиусы не превышают высоты треугольника, то есть \({\sqrt3}/{2}\) (рис. 5).

Рис. 5.
С учетом этих наблюдений поступим следующим образом. Покроем данный нам квадрат одинаковыми равносторонними треугольниками со стороной 1 и поместим в вершины треугольников круги, радиусы r которых удовлетворяют соотношению \({\sqrt3}/{3}<r<{\sqrt3}/{2}\) (радиусы, вообще говоря, могут быть разными, лишь бы каждый из них удовлетворял указанному неравенству). Тогда весь квадрат останется покрыт кругами, но при этом ни одна его точка не окажется накрыта более, чем тремя кругами (рис. 6). Остается заметить, что, покрывая квадрат треугольниками поменьше, мы можем сделать круги сколь угодно маленькими.

Рис. 6.
Важно, что в описанной выше конструкции мы использовали именно треугольную решетку, а не квадратную, то есть накрыли наш квадрат множеством маленьких треугольничков, а не квадратиков. В самом деле, посмотрим, что получится, если мы расположим непересекающиеся круги в вершинах квадрата со стороной длины 1 и начнем их раздувать. Сначала картина будет похожей на то, что мы видели выше в случае треугольника: от непересекающихся кругов через состояние, в котором соседние круги касаются друг друга (их радиус в этот момент равен \({1}/{2}\)) мы приходим к положению, когда в центре имеется незакрытая кругами область, а соседние круги попарно накладываются друг на друга. Однако следующее критическое состояние, соответствующее радиусу \({\sqrt2}/{2}\), в котором все четыре граничные окружности проходят через одну точку, отделяет нас от принципиально новой позиции. Если радиус кругов больше чем \({\sqrt2}/{2}\), они все пересекаются друг с другом, и в квадрате появляется область, накрытая четырьмя кругами, что для решения нашей задачи не поможет (рис. 7).
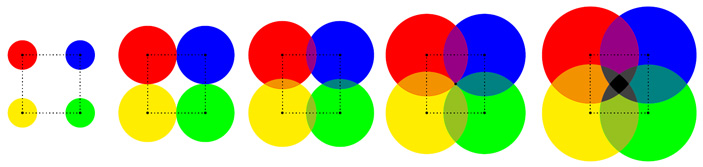
Рис. 7.
Итак, мы построили покрытие (а точнее, семейство покрытий) квадрата кругами, в котором каждая точка квадрата накрыта не более, чем тремя кругами. Таким образом, мы показали, что топологическая размерность квадрата не превышает 2. Убедимся теперь, что она не равна 1, то есть нельзя построить покрытие, в котором каждая точка квадрата накрыта не более, чем двумя кругами. В самом деле, рассмотрим произвольное покрытие квадрата кругами достаточно маленького радиуса (например, меньшего десятой доли длины стороны квадрата).

Рис. 8.
Рассмотрим круг, который накрывает центр квадрата O (желтый круг на рис. 8). Поскольку граница круга самому кругу не принадлежит, то каждая ее точка должна быть накрыта каким-нибудь другим кругом. Так, точка Q граничной окружности накрыта некоторым кругом, который пересекается с первым (зеленый круг на рис. 8). Однако точки пересечения граничных окружностей тоже должны быть чем-то накрыты. Но если топологическая размерность квадрата равна 2, это немедленно приводит нас к противоречию: любой круг, накрывающий точку A, пересекается с обоими кругами и у нас образуется область, накрытая тремя кругами одновременно, чего быть не должно.
б) Если в предыдущем пункте квадратная решетка не привела нас к решению, то здесь она оказывается ключом к успеху. Главным оказывается следующее соображение. Посмотрим на ту часть рис. 7, на которой изображены круги радиуса \({1}/{2}\)). Оказывается, если добавить еще один такой же круг по центру, то любая точка квадрата будет накрыта не более чем двумя кругами, и всего лишь четыре точки окажутся непокрытыми (рис. 9, слева). Или же (что на самом деле то же самое) надо взять другой критический случай из рис. 8 — там в квадрате непокрытой является и вовсе лишь одна точка.

Рис. 9.
Идея теперь заключается в том, чтобы разбить ковер Серпинского на квадраты и покрыть эти квадраты так, чтобы непокрытые кругами точки соответствовали выкинутым областям ковра Серпинского. Так, справа на рис. 9 изображено покрытие кругами, радиус которых равен \({\sqrt2}/{6}\) (длина стороны ковра Серпинского предполагается равной 1). Здесь ковер Серпинского разбит на 8 квадратов, каждый из которых покрыт кругами целиком, за исключением центра. Аналогично для каждого натурального числа n можно разбить ковер Серпинского на \(8^n\) квадратиков и покрыть их кругами по той же схеме — в этом случае радиус кругов будет равен \({\sqrt2}/{(2\cdot3^n)}\). И так как радиус можно сделать сколь угодно малым, это означает, что топологическая размерность ковра Серпинского не превышает 1.
Остается убедиться, что ковер Серпинского не является нульмерной фигурой. Но это совсем просто: например, можно заметить, что ковер Серпинского включает в себя в качестве подмножества отрезок (скажем, нижняя часть исходного квадрата, из которого ковер Серпинского итеративно строился, не была выкинута ни на каком шаге, а значит, в него входит целиком). Последний же, как мы видели, одномерен.
Что касается фрактальной размерности d ковра Серпинского, то вычислить ее тоже не составляет труда. Когда мы разбиваем исходный ковер со стороной 1 на коврики со стороной \({1}/{3}\), всего таких ковриков восемь. Это означает, что должно быть выполнено соотношение \(3^d=8\). Поэтому размерность ковра Серпинского есть \(d=\log_{3}8\approx1{,}8928\). Как видим, размерность получается дробной.
Послесловие
Как было отмечено в самом начале задачи, с интуитивной точки зрения размерность фигуры — это количество параметров, необходимых для того, чтобы точно задать положение любой точки в этой фигуре. Например, поверхность Земли является двумерной, поскольку для определения любого места на карте достаточно двух координат — широты и долготы, а автотрасса Москва — Санкт-Петербург в первом приближении одномерна, поскольку для описания местоположения автомобиля на ней нужен лишь один параметр — расстояние до Москвы (или до Санкт-Петербурга). С точки зрения классической механики мы живем в трехмерном пространстве или, если его дополнить временной осью, в четырехмерном пространстве-времени.
Математики, естественно, умеют работать и с объектами больших размерностей: n-мерное (линейное) пространство — это просто множество всевозможных наборов из чисел вида \((x_1,x_2,\ldots,x_n)\), называемых векторами. Каждый такой вектор отвечает некоторой точке этого пространства, и для задания каждой точки нужно ровно n параметров-координат. Более сложный вопрос возникнет, если мы возьмем произвольное подмножество и спросим, какова размерность у него. Способ, который надо брать на вооружение, чтобы ответить на этот вопрос, зачастую зависит от свойств подмножества, на которых мы сфокусируем свое внимание, которые для нас по тем или иным причинам являются важными. От способа же, порой, зависит результат, который в итоге будет получен, — об этом наша задача.
Наиболее естественным понятие размерности получается в том случае, когда рассматриваемые нами подмножества ограничены рядом структурированных условий. Например, пространства, изучающиеся в рамках линейной алгебры, наделены сложением и умножением на числа. При этом допустимо рассматривать только такие подпространства, которые замкнуты относительно этих операций, то есть, скажем, сумма двух векторов подпространства должна тоже быть элементом этого подпространства. В этих условиях размерностью оказывается число элементов в базисе подпространства, то есть, грубо говоря, все то же количество независимых параметров, необходимых для того, чтобы задать произвольный вектор.
Ситуация становится более сложной, если мы переходим к произвольным метрическим и топологическим пространствам. Один из вариантов определить понятие размерности — топологическую размерность — мы уже видели выше. Другой способ — индуктивная размерность — опирается на то соображение, что размерность «сферы» в n-мерном пространстве равна \((n-1)\). В самом деле, окружность, лежащая в плоскости, одномерна, стандартная сфера, находящаяся в трехмерном пространстве, двумерна, а в общем случае сфера задается уравнением \(x_1^2+x_2^2+\ldots+x_n^2=r^2\), и легко видеть, что она имеет в точности \((n-1)\) независимый параметр: координаты \(x_1,\ldots,x_{n-1}\) можно выбрать любыми, а \(x_n\) по ним уже определяется однозначно. Сообразно с этим наблюдением определим размерность фигуры следующим образом: для дискретных множеств (таких, как конечный набор точек) размерность будет равна нулю. «Вытягивая» нульмерный объект в некотором направлении, мы получим одномерное множество. Затем, «вытягивая» одномерный объект в новом направлении, получим двумерное множество, и так далее. Аналогия здесь такая: граница n-мерного множества является \((n-1)\)-мерным, как, например, граница (двумерного) круга — это (одномерная) окружность, а граница (трехмерного) шара — (двумерная) сфера.
Более точно, имеется две индуктивные размерности пространства \(X\) — большая \(\mathrm{Ind}(X)\) и малая \(\mathrm{ind}(X)\). Строго они определяются следующим образом. Во-первых, размерность пустого множества равна \(-1\), таким образом имеет место равенство \(\mathrm{Ind}(\emptyset) = \mathrm{ind}(\emptyset) = -1\). Затем, индуктивно, \(\mathrm{ind}(X)\) есть наименьшее целое n такое, что для каждого \(x\in X\) и для каждого открытого множества \(U\), содержащего \(x\), существует такое открытое множество \(V\), содержащее \(x\), что замыкание \(\overline{V}\) является подмножеством \(U\), а размерность границы \(\partial V\) не превышает \((n-1)\). Что же касается большой индуктивной размерности, то для нее условие несколько более строгое: \(\mathrm{Ind}(X)\) есть наименьшее целое n, для которого для любых открытого \(U\subset X\) и замкнутого \(F\subset U\) существует открытое \(V\) такое, что \(F\subset V\), \(\overline{V}\subset U\) и размерность \(\partial V\) не превышает \((n-1)\). Очевидно, \(\mathrm{ind}(X)\leqslant\mathrm{Ind}(X)\); кроме того, \(\mathrm{dim}(X)\leqslant\mathrm{ind}(X)\), где \(\mathrm{dim}(X)\) обозначает топологическую размерность пространства. Для всех «достаточно хороших» множеств все эти три размерности совпадают, однако существуют примеры, когда неравенства становятся строгими. Например, существует серия так называемых бикомпактов \(X_n\), для которых \(\mathrm{dim}(X_n)=1\), \(\mathrm{ind}(X_n)=n\), \(\mathrm{Ind}(X_n)=2n-1\).
Однако бывают случаи, когда и вышеперечисленных понятий становится мало. Часто так происходит в тех ситуациях, когда изучаемые объекты имеют одну и ту же, скажем, топологическую размерность, но явным образом непохожи друг на друга. Так, например, невооруженным взглядом видно, что обычная прямая линия, кривая Дракона и снежинка Коха заметно различаются — первая «почти не занимает места», вторая, напротив, заметает всю плоскость, а третья занимает промежуточное положение между ними. Тем не менее, топологическая размерность каждой из них составляет 1. С целью все-таки как-то отличить подобные объекты друг от друга был придуман ряд понятий размерности, базирующихся на идее масштабируемости. Такова фрактальная размерность, (размерность Хаусдорфа) которую мы уже видели выше: несложно убедиться, что фрактальные размерности прямой линии, кривой Дракона и снежинки Коха равны 1, 2 и \(\log_34\) соответственно. Другой пример доставляет грубая размерность (размерность Минковского).
Грубая размерность множества \(X\) определяется следующим образом. Для каждого \(\varepsilon>0\) рассмотрим минимальное число \(N_{\varepsilon}\) кругов (шаров) диаметра \(\varepsilon\), которыми можно покрыть \(X\). Тогда грубая размерность представляет собой предел \(\mathrm{dim}_{\mathrm{box}}(X)=\lim\limits_{\varepsilon\to0}\dfrac{\ln(N_{\varepsilon})}{-\ln(\varepsilon)}\). Если же предела не существует, то говорят о верхней и нижней грубой размерностях как о верхнем и нижнем пределе соответствующего выражения. В таком представлении грубая размерность ничем не отличается от фрактальной размерности, «наивное» определение которой мы дали выше. Строгое определение фрактальной размерности множества \(X\) таково: сначала для каждого \(S\subset X\) и для каждого \(d\geqslant0\) рассмотрим множество
Затем нужно взять \(\inf\limits_{d>0}\{d\colon C_d(S)=0\}\) — это и будет фрактальная размерность. Оказывается, нижняя грубая размерность множества всегда не меньше его фрактальной размерности, которая, в свою очередь, не меньше малой индуктивной размерности.
При подготовке статьи была использована книга П. С. Александрова и Б. А. Пасынкова «Введение в теорию размерности».
Из Википедии – «…Основная идея «дробной» (англ. fractured) размерности имеет долгую историю в области математики, но именно сам термин введён в оборот Бенуа Мандельбротом в 1967 году в его статье[en] о самоподобии, в которой он описал «дробную» (англ. fractional) размерность[3]. В этой статье Мандельброт ссылался на предыдущую работу Льюиса Фрайя Ричардсона, описывающую противоречащую здравому смыслу идею о том, что измеренная длина береговой линии зависит от длины мерной палки (шеста)».
Скажем, инженер не посчитает противоречащей здравому смыслу идею о том, что измеренная длина береговой линии зависит от длины мерной палки, и добавит, – …в жизни всё будет зависеть от человеческой цели практической задачи измерения с заданной точностью.
Последние задачи















Рис. 1. Покрытия отрезка кругами разных радиусов