Вперед в прошлое
Одно из самых интригующих предсказаний в космологии и общей теории относительности — это существование космических струн, одномерных топологических дефектов нашего пространства, которые теоретически могли образоваться в ранней Вселенной.
Если представить, что мы живем на плоскости, то струна представляет собой точку (или перпендикулярную к плоскости прямую), из-за наличия которой часть пространства словно выкидывается, а пространство склеивается обратно по границе выкинутой части (рис. 1). В результате такого дефекта два луча, которые вышли из одного объекта (скажем, далекого квазара) в разных направлениях, могут сойтись обратно. При этом они будут двигаться по прямым, пройдут по разные стороны от струны и создадут два разных изображения квазара.

Здесь надо быть несколько осторожным в словах, так как такой эффект — это не совсем гравитационное линзирование в понимании общей теории относительности, возникающее из-за искривления пространства массой. На самом деле пространство вокруг струны абсолютно плоское, и никакой эффективной массы и, соответственно, гравитационной силы статичные наблюдатели не почувствуют. Этот эффект — чисто топологический, связанный с геометрическим дефектом пространства.
Одним из удивительных следствий эффекта «линзирования» является возможность путешествия «быстрее» света. На рис. 1 изображены два пути от одного и того же квазара к Земле, причем один из путей короче другого.
Давайте для определенности предположим, что один более длинный путь равен 10 световым годам, а более короткий — 5. Тогда наблюдатель, который движется по второму пути со скоростью, скажем, 0,8 скорости света (что вполне возможно) придет к Земле раньше (через 6,25 лет), чем свет, который двигался по первому пути (10 лет). Несмотря на всю парадоксальность, такой эффект не просто возможен, он наблюдался (подробнее об этом в послесловии)!
Получается, что ракета может «вылететь» из квазара позже светового пучка, но, выбрав более короткий путь, тем не менее долететь до Земли раньше этого самого пучка. Такие «сверхсветовые» траектории называются пространственно-подобными. В обычной геометрии движение по таким траекториям невозможно, так как оно предполагает движение быстрее скорости света.
Обычно говорят, что два события отделены пространственно-подобным отрезком, если эти события никак теоретически не могут повлиять друг на друга (сигнал не может идти быстрее света по пространственно-подобной траектории). К примеру, два взрыва на расстоянии 10 световых лет друг от друга произошедшие с разницей в 5 лет: такие два события никак не могут повлиять друг на друга в обычном пространстве без дефектов. Замечательным свойством таких событий является то, что всегда можно найти такого наблюдателя (движущегося с определенной скоростью), для которого эти два события происходят одновременно.
Если вам этот факт не знаком, не беспокойтесь, в послесловии будут даны все пояснения. А пока примите это как данность.
В частности, в случае с космической струной, так как траектория по короткому пути №2 «быстрее», чем движение света по длинному пути №1, этот путь будет пространственно-подобным. И поэтому, для некоторого наблюдателя, движущегося с определенной скоростью (которая меньше скорости света, естественно) относительно струны по пути №1, вылет космического корабля из квазара и прилет на Землю будут одновременными событиями!
Можно ли использовать такой красивый эффект космических струн в наших корыстных целях? Давайте несколько усложним геометрию: пусть есть две космические струны (рис. 2). В таком случае есть два коротких маршрута №1 и №3 (они оба короче чем прямой путь №2).

Рис. 2. Геометрия пространства с двумя космическими струнами. Рисунок из книги Welcome to the Universe
Задача
После обнаружения потенциально обитаемой планеты B за пределами двух космических струн, экспедиция из планеты A отправилась изучать ее. Позже оказалось, что планета B абсолютно непригодна для жизни, а хитрый капитан экспедиции решил вернуться в прошлое и предостеречь себя и команду от обреченной на провал экспедиции.
Возможно ли такое? Если да, то при каких условиях и какие инструкции нужно дать капитану? Если нет, то как можно объяснить невозможность?
Подсказка 1
Что если струны не покоятся, а движутся? Меняет ли это что-нибудь? По сути, движение наблюдателя относительно струны или движение струны относительно наблюдателя — одно и то же.
Подсказка 2
Попробуйте воспользоваться свойством пространственно-подобных траекторий. Если трюк работает один раз, то его можно повторить и второй.
Решение
Несмотря на то, что задача приурочена к первому апреля, никакого подвоха здесь нет. Такое путешествие вперед в прошлое действительно теоретически возможно, и было описано в статье Дж. Р. Готта Closed timelike curves produced by pairs of moving cosmic strings: Exact solutions в 1991 году. Давайте поймем как это возможно.
Итак, есть два события, связанные пространственно-подобным интервалом: экспедиция отправляется с планеты A и долетает до планеты B по пути №1 (см. рис. 2). Интервал пространственно-подобный, так как свет по прямому пути №2 от A до B будет добираться дольше, чем космический корабль по пути №1. Так как интервал пространственно-подобный, то можно найти наблюдателя, движущегося с определенной скоростью по пути №2 (влево), которому кажется, что эти два события (вылет с A и прилет на B) произошли одновременно. Назовем этого наблюдателя Марти.
На всякий случай, повторим: для Марти, летящего с большой скоростью влево, как бы парадоксально это ни звучало, экспедиция одновременно отправляется с планеты A и прибывает на планету B. Заметим, что по сути ничего не изменится, если вместо летящего влево Марти вправо будет лететь струна №1: это все равно, что пересесть в новую систему отсчета. Значит, покоящемуся (в любой точке пути №2) на месте Марти (при летящей вправо струне) эти два события также будут казаться одновременными.
Трюк можно повторить, вернувшись теперь из планеты B обратно на планету A по пути №3 (то есть вокруг второй струны). И, опять же, если вторая струна движется влево с определенной скоростью, Марти будет казаться, что вылет экспедиции из планеты B происходит одновременно с ее прилетом обратно на планету A.
Получается, что, если две струны движутся очень быстро в противоположных направлениях, то для покоящегося наблюдателя три события — начало экспедиции на планете A, ее прилет на планету B (по пути №1) и возврат обратно на планету A (по пути №3) — происходят одновременно!
На рис. 3 показано, как будет выглядеть такое путешествие с точки зрения уже покоящегося Марти. Траектории объектов на таких диаграммах часто называют мировыми линиями. У покоящегося в одном месте объекта мировая линия — это просто вертикальная прямая, так как он «движется» только во времени. Из-за того, что струны летят в противоположных направлениях, их мировые линии — это две скрещивающиеся прямые. Если «разрезать» эту диаграмму горизонтальной плоскостью на какой-нибудь высоте, получится срез во времени: мгновенный снимок пространства в определенный момент времени. Таким образом, два события, расположенные на одной горизонтальной плоскости, происходят одновременно.

Рис 3. Схема путешествия во времени с двумя быстро летящими в противоположных направлениях струнами. На этой схеме время течет вдоль вертикальной оси, а пространство двумерно. Рисунок из книги Welcome to the Universe
В итоге получаем такой план экспедиции. Она стартует с планеты A (вертикальная линия обозначает, что экспедиция находилась на этой планете некоторое время до старта). До вылета капитан видит себя из будущего, только что прилетевшего с планеты B. Затем он облетает вокруг движущихся струн до планеты B, находясь на горизонтальной плоскости (поскольку для покоящегося Марти его вылет и прилет обратно происходят в один и тот же момент времени). Затем он возвращается обратно на планету A и встречает себя из прошлого.
Послесловие
Как бы парадоксально и противоестественно это ни звучало, теоретически такое путешествие вполне возможно в рамках общей теории относительности. Дело в том, что все законы в ОТО (в том числе закон сохранения энергии и принцип причинности) носят чисто локальный характер. Иными словами, в плоской геометрии без каких-либо дефектов и особенностей (например, если пространство пустое, или если мы рассматриваем законы вблизи свободно падающего наблюдателя) действительно все должно сохраняться и быть причинно-связным. Однако в общем случае это не так: пространство-время может иметь какие угодно странности.
Другим примером путешествия во времени с помощью нетривиальной геометрии пространства является двигатель Алькубьерре (см.: M. Alcubierre, 1994. The warp drive: hyper-fast travel within general relativity), который определенным образом искажает пространство, «подтягивая» его под космический корабль, что позволяет путешествовать с абсолютно любой скоростью. Еще один пример — кротовые норы, которые могут связывать две сколько угодно удаленные части Вселенной. С помощью таких типов геометрических экзотик можно вполне путешествовать во времени (например, для двигателя Алькубьерре это описано в статье A. E. Everett, 1996. Warp drive and causality).
Стоит отметить, что в решении Готта, так же, как и во всех остальных экзотических геометриях, где возможно путешествие во времени, есть небольшой нюанс. Путешествие во времени возможно не всегда, а только внутри некоторой области (на рис. 3 это область снаружи синих конусов). Иными словами, нельзя путешествовать «бесконечно» назад в прошлое.
Существование такой ограниченной области — горизонта Коши — общее свойство таких странных геометрий. Если представить, что мы каким-то образом создали машину времени (с помощью двух движущихся струн, или варп-драйва Алькубьерре) в 2100 году, то мы не сможем, скажем, из 2150 года «прилететь» обратно в 2018-й (сможем прилететь только в момент после 2100 года). Это, в частности, объясняет известный парадокс Хокинга о том, почему мы не встречаем путешественников во времени.
Существуют ли струны на самом деле? На данный момент никаких доказательств существования космических струн нет, однако есть очень строгие ограничения (из наблюдений и теории возникновения Вселенной) на число таких струн в обозримой Вселенной.
Тем не менее, явно же должен быть какой-то подвох? Невозможно же просто так взять и путешествовать во времени, даже с такими ограничениями? А как же глобальная причинность?
Здесь и правда есть некоторая загвоздка. Дело в том, что пока мы рассматривали чистую кинематику — движение материальных точек в какой-нибудь сложной геометрии пространства-времени. Но мир не состоит из вакуума и материальных точек, он состоит из полей и возбуждений в них. Дело в том, что если подключить к рассмотрению помимо искривленного пространства-времени (то есть гравитации) еще и квантовые поля (из которых мы с вами состоим), а затем попытаться проделать тот же анализ, то картина немного усложняется.
Проблема в том, что в искривленном пространстве-времени вакуум — не совсем вакуум: если изначально пустое пространство искривлено, то наблюдатель может видеть (регистрировать) частицы, рожденные из вакуума. В плоском пространстве это тоже происходит — виртуальные частицы постоянно рождаются и уничтожаются, но баланс никогда не нарушается, и реальных частиц мы не видим. Однако в искривленном пространстве этот баланс нарушается. Например, вблизи горизонта черной дыры могут рождаться частицы из вакуума (излучение Хокинга). А на горизонте Коши (в случае с геометрией двух струн) может существовать некий аналог хокинговского излучения из вакуума.
В частности, для двигателя Алькубьерре «простые» расчеты показывают (S. Finazzi et al., 2009. Semiclassical instability of dynamical warp drives), что это излучение может быть бесконечно интенсивным в момент формирования горизонта, и «уничтожит» все, что находится внутри капсулы. «Простые» эти расчеты в том смысле, что они основаны не на самостоятельной теории квантовой гравитации, которая просто необходима для согласованных результатов, а на полу-классическом методе: теория поля на фоне (!) искривленного пространства-времени (то есть реакция геометрии на поля не учитывается, они отделены друг от друга, что не совсем физично). Поэтому, конечно, к таким результатам стоит относиться с осторожностью.
Но, тем не менее, это дает некий намек на то, что, несмотря на нашу хитрость в попытках обмануть время, природа в итоге может оказаться хитрее нас.
Задача основана на работах Джона Ричарда Готта по геометрии пространства в присутствии космических струн.
Справка по специальной теории относительности
Чтобы понять, почему для любых двух событий, которые отделены друг от друга пространственно-подобным интервалом, можно найти наблюдателя, для которого эти события происходят одновременно, давайте обратимся к диаграммам из специальной теории относительности, одна из которых показана на рис. 3. На Youtube-канале minutephysics есть отличное видео про то, как стоит думать о таких диаграммах:
На рис. А (слева) изображена такая диаграмма: по вертикальной оси отложена координата времени (когда произошло событие), по горизонтальной — пространственная координата (где произошло событие). Для удобства будем измерять время в годах, а длину — в световых годах (это расстояние, которое свет проходит за год).


Рис. A. Слева — диаграмма событий с двумя времени- и пространственно-подобными областями. Справа — одновременные и неодновременные события
События, время до которых (в годах) больше чем расстояние до них (в св. годах), называются времениподобными, а события, до которых время меньше, — пространственно-подобными. Отличие этих событий состоит в том, что на пространственно-подобные события (они в красной области на диаграмме) мы никак повлиять не можем, так как для этого пришлось бы отправить сигнал, который должен будет лететь быстрее света, а это невозможно. К примеру, на рис. А (слева) красная точка снизу — именно такое событие. Оно произойдет через 2 года на расстоянии 10 св. лет от нас. И чтобы повлиять на это событие, потребовалось бы двигаться со средней скоростью 5c (то есть в 5 раз быстрее скорости света).
С другой стороны, легко показать, что на события в синей области мы повлиять можем. Зеленая линия, идущая под углом 45°, — это световая линия, которая показывает как распространяется свет: за 10 лет он проходит 10 св. лет. Соответственно, линии под меньшим углом к оси x соответствуют сверхсветовым скоростям, под большим — досветовым.
События называются одновременными, если их координаты по времени равны. Пример показан справа на рис. А: два нижних события происходят в одно и то же время t1 и для нас они одновременны.
Однако одновременность в специальной теории относительности вещь не абсолютная: два одновременных события в одной системе отсчета могут оказаться неодновременными в другой. На рис. Б показан именно такой пример.
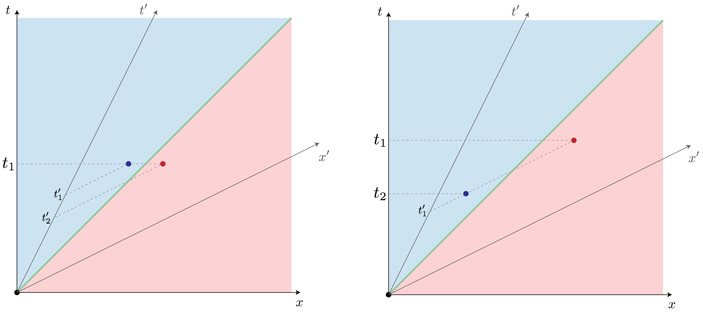

Рис. Б. Два одновременных в системе (t, x) события (слева) оказываются неодновременными в системе (t′, x′) и наоборот (справа). Пунктирные линии проведены параллельно осям x и x′
В системе (t, x) два события происходят в одно и то же время t1. При этом для наблюдателя в системе (t′, x′), которая движется с определенной скоростью относительно начальной системы, эти два события оказываются неодновременными из-за того, что оси сжимаются (можно показать, чем больше скорость, тем больше сжатие осей к световой линии). У minutephysics есть подробное видео, почему именно так происходит:
Обратная ситуация показана на рис. Б справа: два одновременных события для наблюдателя в системе (t′, x′), случившиеся в момент t′1, происходят неодновременно для наблюдателя в системе (t, x).
Возникает вопрос: а для любых ли двух событий A = (tA, xA) и B = (tB, xB) можно подобрать такую систему отсчета (то есть такую скорость наблюдателя), для которой два события будут происходить одновременно: \( t_A'=t_B'\)?
Оказывается, что нет. Глядя на рис. В, и следуя логике, изложенной выше, можно легко убедиться, что для событий, соединенных красными интервалами (угол которых с осью х больше 45°), это невозможно сделать, тогда как для событий, соединенных синими интервалами, это возможно. Красные интервалы на этом рисунке, таким образом, оказываются времениподобными, а синие — пространственно-подобными. Если два события отделены пространственно-подобным интервалом, то одно никак не можем повлиять на другое!
Рис. В. События, отделенные пространственно-подобными (синие) и времениподобными (красные) интервалами
-
По идее, возврат экспедиции должен произойти не одновременно с её стартом, а произойти на некоторое время раньше (чтобы можно было успеть передать информацию).
То есть, Марти в точке А сначала будет видеть 1 корабль, потом ближе к моменту возврата экспедиции из одной точки появится сразу 2 корабля, один из которых очень быстро полетит по спирали задом наперёд, а второй сядет рядом с точкой А. Затем летящий задом наперёд корабль врежется в исходный, уже стартовавший, корабль и они "аннигилируют". Так?-
Ну можно сделать эти моменты (в зависимости от скорости полёта струн, например) сколь угодно близко по времени. А почему аннигилируют?
-
А если взлёт и посадка произойдут в точке А в один момент времени, то в этот момент наблюдатель увидит окружность, которая тут же исчезнет.
-
Задачу нужно упростить. Например, слетать на планету В, что находится за 1000 св. лет от Земли и вернуться через неделю после старта. Отчитаться о том, что планета В непригодна для жизни. Для этого и одной струны хватило бы.
А так, больше вопросов, чем ответов. Информацию получили, и ничего за это не заплатили. А если на корабле бунт и один космонавт зарезал другого? И начинается котовасия с дедушкой..
-
-
Перечитал еще раз Послесловие, так и не нашел там про то, где такой эффект наблюдался.
-
Да, прошу прощенья, в итоге я не написал про это, так как это было бы слишком много и не имело прямого отношения к делу.
Речь о вот этом наблюдении (https://arxiv.org/pdf/astro-ph/9610162.pdf): там идентифицируется одно и тоже событие происходящее в квазаре QSO 0957+561, но которое мы наблюдаем с разницей в 415 дней.
Это объясняется тем, что свет от одного и того же событие доходит до нас двумя разными путями из-за обычного гравитационного линзирования на тёмной материи, и один оптический путь получается на 415 световых дней короче.
-
Нафиг-нафиг... Прежде чем браться за предложенную задачу, нужно рассмотреть другую. Как астронавту вернуться в его же собственное локальное время? Скажем, слетать за 500 св. лет и вернуться через неделю, чтобы узреть своих коллег живыми и невредимыми? Так как с путешествием в один конец в теории относительности проблем не возникает, главная польза от искривленных пространств - путешествие в оба конца. А от машины времени один только вред.
Если вы будете использовать ОТО вместо СТО, то станет ещё хуже. Т.к. именно ОТО постулирует искривления пространства, из-за которых все проблемы.
Можно как автор задачи, потребовать чтобы окончательный ответ удовлетворял не только ОТО, но и квантовой физике. Авось, противоречия сами исчезнут.
Замкнутые времениподобные кривые изначально воспринимались как какой-то косяк, от которых надо избавиться путём допиливания ОТО. Но время идёт. ОТО дополняют все кому не лень (теми же струнами, например), но ничего хорошего не получается. Вроде просто застой в науке, ничего страшного. Но послушаешь современных физиков, и окажется, что уже многие из них готовы согласится с возможностью путешествий во времени. Хотя что-нибудь более лженаучного мне представить тяжело. Выводы неутешительны: физика, как наука, давно и уверенно деградирует...
-
-
-
1. > СТО прекрасна, пока её используют в бесконечном Евклидовом пространстве.
СТО пишется в пространстве Минковского, не в Евклидовом. Там определена абсолютно другая норма.
2. СТО вообще не имеет отношения к физике пространства-времени, это чисто кинематическая теория движения.
3. Пока абсолютно никаких отклонений от ОТО науке не известно. ОТО работает на катастрофически точных масштабах.
4. То, что ОТО не исключает путешествия во времени, не значит, что такое возможно (как я и писал выше). В самом этом факте ничего плохого нет.
5. > Замкнутые времениподобные кривые изначально воспринимались как какой-то косяк
Наверное, пространственно-подобные?
6. > Замкнутые времениподобные кривые изначально воспринимались как какой-то косяк, от которых надо избавиться путём допиливания ОТО
Это утверждение неверное. ОТО допиливают далеко не за тем.
7. В последнем абзаце я вообще не понял логики? Да, есть некоторые проблемы, мы знаем и понимаем далеко не всё. Но ОТО - это на сегодняшний момент лучшая теория гравитация, потдверждённая столетием разных самых точных экспериментов (LIGO вам в пример). Не понимаю, что вы можете иметь против этого и зачем?-
1. Пространство Минковского строится из трёхмерного Евклидова, добавлением четвёртой размерности-времени. Если же в качестве базового трёхмерного пространства использовать любое другое кривое, то начинаются проблемы. Например, можно легко подобрать пространство так, чтобы можно было бы повторить парадокс близнецов, не выходя за пределы инерциональных систем.
2. СТО нужно было для того, что бы наглядно проиллюстрировать причину проблем ОТО.
3. Не спорю.
По остальным пунктам. Из того, что ОТО не исключает путешествия во времени, можно сделать один из трёх выводов:
а) Путешествия во времени возможны. И тогда мы обязаны переделать свою логику, а затем всю физику.
б) ОТО не верна, т.к. например, она некорректно искривляет пространство. И тогда мы обязаны пересмотреть ОТО и возможно СТО.
в) Мы вышли за границу применимости ОТО. Тогда нужно установить эти границы. Только современные представления о чёрных дырах, об эволюции вселенной и другие самые интересные вещи скорее всего окажутся вне компетенции ОТО.
Каждый может выбрать тот вывод, который он считает наиболее правильным. Но у меня сложилось впечатление, что многие готовы признать возможность путешествия во времени, но не для того, чтобы пересмотреть всё. А наоборот, что бы всё оставить как есть.
-
-
-
С уважением!
-
Надо понимать, что, безусловно, задача идеализирована. К ней стоит относится скорее как к полёту материальных точек, нежели как к реальной физической задаче.
С точки зрения капитана всё будет выглядеть обычно: время в его системе летит обычным образом. Но надо понимать, что система отсчёта капитана - неинерциальная, он постоянно ускоряется, тормозит и т.д. В таких системах всякие квантовые эффекты начинают играть роль, и он может видеть, скажем, частицы, просто рождающиеся из вакуума и прочие вещи.
Последние задачи
















Рис. 1. Схематическое изображение влияния космической струны на пространство и эффекта «линзирования». Рисунок из книги Welcome to the Universe