Совершенные магические квадраты

Федор Нилов
«Квантик» №8, 2022

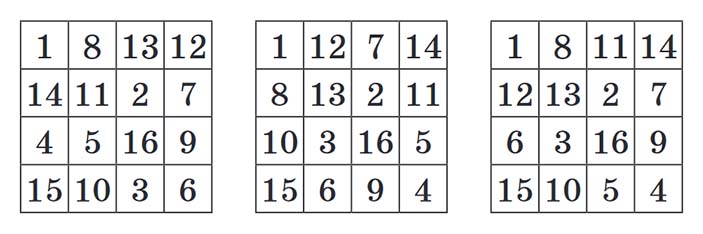
В «Квантике» №7 за 2022 год мы обсуждали магический квадрат Кхаджурахо. Это квадрат 4×4, в котором одинаковы суммы во всех строках, столбцах, двух диагоналях, всех пандиагоналях (каждая такая диагональ состоит из четырёх клеток одного цвета на рисунке справа), а также во всех девяти квадратах 2×2. Назовём квадраты 4×4, для которых выполняются все эти условия, дьявольскими.

Всего дьявольских квадратов 24∙16, но все они получаются из трёх квадратов на картинке ниже такими операциями: сдвиги по горизонтали (крайний столбец переезжает на другую сторону), сдвиги по вертикали, повороты и перевороты.

Существует другой подход к построению дьявольских квадратов. Сначала все числа в квадрате уменьшаются на 1, то есть теперь в квадрате расставляются числа от 0 до 15. Далее каждое число представляется в двоичной системе счисления или, иначе говоря, как сумма степеней двойки. Например, 7=1+2+2². Затем отдельно составляются 4 квадрата 4×4, каждый из которых отвечает за свой разряд, то есть за свою степень двойки. В каждой ячейке такого квадрата стоит или 0, или соответствующая степень двойки. Для каждого квадрата должно выполняться равенство всех рассматриваемых сумм.

В итоге эти 4 квадрата складываются поэлементно. Важно, чтобы в ячейках итогового квадрата встретились все числа от 0 до 15. Пример такого построения указан на рисунке:

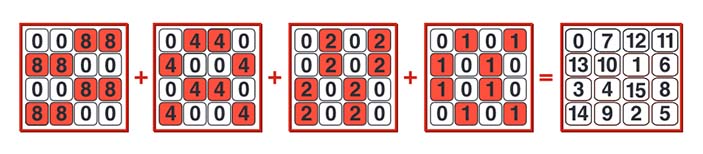
Попробуйте разложить в суммы степеней двойки квадраты в начале заметки и посмотреть, как устроены соответствующие 4 квадрата.

Теперь мы будем расставлять в квадрате n×n числа от 1 до n² . Если суммы чисел в строках, столбцах и диагоналях равны, квадрат называется магическим. Магический квадрат существует для любого n, отличного от 2. Для n=3 он всего один (с точностью до поворотов и симметрий) — квадрат Ло Шу из прошлого номера. Для n=4 и 5 существуют 880 и 275305224 магических квадрата, но уже для n=6 точное значение неизвестно.

Обобщение дьявольских квадратов — совершенные магические квадраты, их впервые рассмотрел
в 1897 году Эмори Мак-Клинток из университета Торонто. Это квадраты n×n, где n кратно 4, в которых

• а) одинакова сумма во всех строках, столбцах, диагоналях, пандиагоналях;
• б) одинакова сумма во всех квадратах 2×2;
• в) сумма чисел в клетках на расстоянии n/2 вдоль одной диагонали равна n²+1.

Пандиагонали получаются так же, как для квадрата 4×4: стартуем из любой клетки и двигаемся вправо-вверх (или вправо-вниз); при этом пересекая границу квадрата мы телепортируемся, как в игре змейка: например, из правого верхнего угла попадаем в левый нижний. На рисунке показана половина пандиагоналей квадрата 5×5.

Отметим, что если склеить из квадрата тор, как мы это делали в прошлой заметке, клетки, фигурирующие в условии в), будут на этом торе противоположными, а пандиагонали ничем не будут отличаться от обычных диагоналей. Для квадратов 4×4 из условия а) автоматически следуют условия б) и в), однако для квадратов больших размеров это не так. С другой стороны, можно показать, что из условий б) и в) следует условие а).

В 1998 году вышла книга «Совершенные магические квадраты», в которой явно описываются все совершенные квадраты и вычисляется их число при фиксированном размере. Авторы — Кэтлин Оллереншоу и Дэвид Бри. Отметим, что первый автор была мэром Манчестера и министром образования при Маргарет Тэтчер, а книга вышла, когда ей было 86 лет.

Художник Алексей Вайнер