Диаграммы Вороного

Артемий Соколов
«Квантик» №7, 2022

Придя домой после школы, Петя обнаружил, что мама купила ему в подарок новый набор цветных карандашей. Как же ему не терпелось их все испытать!

Петя взял белый лист бумаги и каждым карандашом отметил по одной точке. Хм, пишут! Этого ему оказалось мало, и он захотел раскрасить весь лист.

— Но как сделать так, чтобы было красиво и интересно? — задумался Петя. — Наверное, рядом с каждой точкой должны быть точки такого же цвета, правда? Иначе будет рябить в глазах.

И Петя решил сделать так: выбирая каждую точку, надо покрасить её в тот же цвет, что и самая близкая к ней изначальная точка.

— Да, тогда, наверное, будет меньше всего пестрить в глазах. Хм, а у каких-то точек сразу две ближайшие... Возьму для них простой карандаш!

Потратив полчаса на раскрашивание листа бумаги, Петя получил такую картинку:

— А вроде бы красиво, надо маме похвастаться! — И Петя понёс рисунок маме.

— Мама, смотри, что я нарисовал!

— Ух ты, разбиение Вороного, здорово!

— Воро... кого?

— Был такой замечательный математик, Георгий Феодосьевич Вороной. Он жил во второй половине XIX века, в честь него названы такие же картинки, как у тебя. Они называются разбиениями или диаграммами Вороного. Долго рисовал?

— Как со школы вернулся.

— Долго! Давай покажу, как это сделать проще. Кстати, ничего удивительного не заметил на картинке?

— У меня вроде получилось, что у частей прямые границы. А почему так?

— Смотри, давай сначала отметим две точки, назовём их A и B. Теперь проведём серединный перпендикуляр к отрезку AB. Это такая прямая, которая проходит через середину AB и идёт перпендикулярно отрезку. Видишь, он делит весь лист на две части?

— Ага.

— Если мы возьмём точку X в той же части, что и  точка A, то отрезок XA будет по длине меньше отрезка XB. Если, наоборот, мы возьмём точку X в той же части, что и точка B, то тогда отрезок XA будет больше отрезка XB.

— А если X лежит на самом перпендикуляре?

— Тогда отрезки XA и XВ равны.

— А, я понял, это как раз разбиение Вороного для точек A и B, да?

— Именно так!

— Теперь попробуем взять три точки A, B и C. Если мы хотим покрасить точку X в такой же цвет, что и A, у нас должны выполняться одновременно неравенства XA < XB и XA < XC. Для этого надо пересечь серединные перпендикуляры к AB и AC и взять соответствующую область — это будет часть, содержащая точку A. Чтобы получить всё разбиение Вороного, надо провести все три перпендикуляра.

— Ой, у тебя серединные перпендикуляры в одной точке пересеклись, это всегда так?

— Да! Про это даже есть теорема в любом школьном учебнике геометрии. А точка пересечения будет ещё и центром окружности, проходящей через все вершины треугольника.

Теорема. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, которая является центром его описанной окружности.

— Теперь давай возьмём сразу много точек и одну из них назовём A. Посмотрим на серединные перпендикуляры тех отрезков, один конец которых совпадает с A. Каждый такой перпендикуляр делит плоскость на две половины. Возьмём все половины, содержащие А, и пересечём их. Часть с точкой А готова.

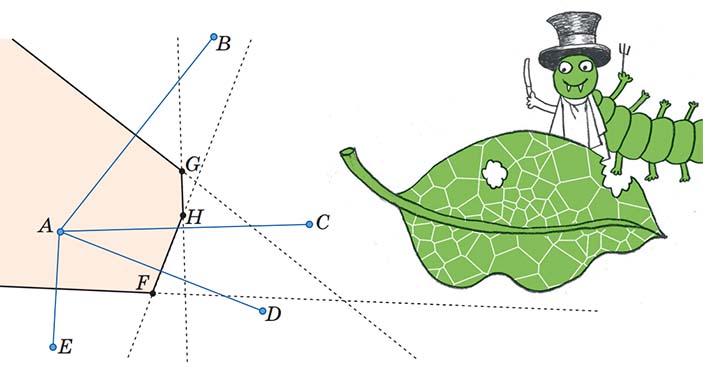
— Ух ты, получается прямо моя картинка! И я даже понял, как это доказать.

— Интересно, что диаграммы Вороного можно увидеть в неожиданных местах: на панцире черепахи, на коже жирафа, в кронах деревьях и даже на листьях дерева. Kак пойдём гулять, обязательно покажу.

— Здорово! — обрадовался Петя и решил ещё порисовать диаграммы Вороного. Попробуйте и вы (например, по ссылке онлайн)!

Художник Артём Костюкевич