Гири в пиалах

Андрей Саускан
«Квантик» №6, 2021

Однажды падишах пригласил Ходжу Насреддина в гости. Приглашение выглядело так. Стражники схватили Ходжу на базаре и, не дав допить шербет, поволокли во дворец, для убедительности пуская в ход кулаки. Ожидавший во дворце падишах сам снизошёл до беседы с известным возмутителем спокойствия.

— До меня дошли слухи, что ты на каждом углу распространяешь клеветническую и конспирологическую информацию о том, что я якобы плохо умею разгадывать головоломки. Да, у меня и правда тяжеловато со свободным временем. То подданные сбегают от налогов во враждебную Месопотамию, то сами сборщики налогов сматываются с собранными налогами туда же. Так у меня скоро не останется ни подданных, ни, хуже того, налогов. А тут ещё твои лживые измышления! Разве можно такое терпеть? Вот я и решил поступить по справедливости: сам загадаю тебе такую головоломку, что с тебя семь потов сойдёт, прежде чем ты с ней справишься. В случае успеха получишь кошелёк с золотыми монетами и будешь отправлен... думаю, в ту же Месопотамию. А не сумеешь — что ж, одним клеветником станет меньше. Если голова не соображает — её надо поскорее отделить от туловища, чтобы спасти оставшийся организм.

— О, сколь трогательна забота великого падишаха о моём никчёмном здоровье! — искренне восхитился Насреддин. — И какую же головоломку предложит мне светлейший?

Рис. 1

— Сейчас узнаешь. Видишь эти девять пиал, расположенных в виде квадрата 3 × 3 (рис. 1)?

— Вижу.

— А вон в сторонке стоят девять гирек массами 1, 2, 3 и так далее вплоть до 9 мискалей^*. И надо разложить эти гирьки по пиалам так, чтобы...

— ...массы по всем рядам, то есть горизонталям, вертикалям и двум большим диагоналям, были одинаковы! — подхватил Насреддин. — Верно? Сейчас покажу, как это делается, и отправлюсь с кошельком золота за рубеж. Ибо мне эта задача известна, и я всегда готов поделиться секретами её решения с несведущими.

— Ишь, какой скорый! — воскликнул падишах. — За кого ты меня принимаешь? То, о чём ты тут начал говорить, мне известно не хуже, чем тебе. Как добиться равенства весов по всем рядам, показали ещё древние китайцы. Не стану утверждать, что я самолично видел тот черепаший панцирь, на котором ими был нацарапан ответ, но я всё-таки его знаю. Нет, моя задача другая, и её так легко ты не одолеешь. Слушай: надо разложить гирьки по пиалам так, чтобы в каждом из восьми названных тобой рядов суммарная их масса (в мискалях) не делилась на 3. Понял?

— Понял... — озадаченно протянул Насреддин.

— Тогда за дело! — подытожил падишах. — Даю тебе... скажем, два часа, чтобы, если придётся, успеть провести казнь ещё засветло. Приступай. И не пытайся бежать — в дверях стража, на окнах решётки.

С этими словами падишах удалился, злорадно посмеиваясь, что Насреддину совершенно не понравилось. Лишь собрав всю волю в кулак, он заставил себя рассуждать — строго и последовательно.

«С чего начать? Конечно, с делимости на 3. Возьмём любую гирьку массой больше трёх мискалей. Если её массу уменьшить на 3 мискаля — что это поменяет? А ведь ничего! Масса любого ряда, содержащего пиалу с этой гирькой, уменьшится на 3, то есть делимость на 3 не изменится. Что это даёт? Упрощение условия. В самом деле, будем уменьшать массы всех гирек на 3 мискаля, пока это возможно. К чему мы придём? У нас будет по три гирьки массой 1, 2 и 3 мискаля — всё-таки чуть проще.

Далее, какие гирьки могут стоять в одном ряду? Понятно, что три одинаковые — точно не могут. Но ведь и три разные не могут — их суммарная масса составит 1 + 2 + 3 = 6 мискалей, что делится на 3. Значит, в каждом ряду ровно две гирьки одинаковой массы. Что это даёт? А ведь немало. Гирек каждого веса по три штуки, и в каждой горизонтали должно быть по две гирьки одинакового веса. Значит, в какой-то горизонтали две одномискалевые гирьки, в другой — две двухмискалевые, в третьей — две трёхмискалевые. То же относится и к вертикалям. Получается, что три любые одинаковые гирьки — вершины своеобразного «прямоугольного треугольника»: одна из них как бы вершина прямого угла, а остальные две гирьки расположены с ней в одной вертикали и одной горизонтали (они — как бы вершины острых углов).

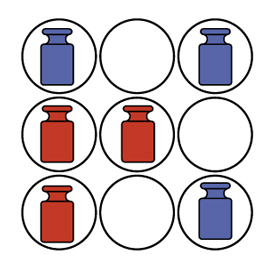
Рис. 2

Хорошо, продолжим. На каждой из двух диагоналей тоже есть пара одинаковых гирек, и тогда эти две пары — «гипотенузы» двух равнобедренных треугольников. Гипотенуза может быть короткой (её гирьки в двух соседних пиалах) или длинной (её гирьки в двух угловых пиалах квадрата 3 × 3). Два этих треугольника не могут быть оба с длинной гипотенузой (каждый занял бы три угловые пиалы) и не могут быть оба с короткой (каждый занял бы центральную пиалу). Значит, один будет с длинной гипотенузой и займёт три угловые пиалы, другой — с короткой, он займёт центр, 4-ю угловую пиалу и соседнюю с ней пиалу на стороне (рис. 2). Но тогда во второй стороне, содержащей 4-ю угловую пиалу, будут три гирьки разной массы, и сумма их масс делится на 3. Противоречие!

Каков же итог? Он однозначен: разложить гирьки требуемым образом невозможно! Откуда вытекает следствие: не сносить мне головы. Как быть?»

Ходжа Насреддин встал и прошёлся по помещению, осторожно проверив надёжность решёток. Крепко, не вылезешь. Он снова задумался, надеясь найти ошибку в своих рассуждениях и многократно припоминая условие. И когда до наступления срока оставалось не больше пяти минут, его осенило.

— Как же я сразу не сообразил? — вслух спросил сам себя Насреддин. — Ничего, и сейчас не поздно.

С этими словами он разложил гирьки по пиалам в полном соответствии с требованиями падишаха.

«И кошелёк с золотом мне тоже никак не повредит», — подумал он.

Дорогие читатели! Попробуйте догадаться, как нашему герою удалось решить заковыристую головоломку. А если не сумеете — посмотрите ответ.

Ответ

Рис. 3

Падишах требовал разложить гирьки по пиалам, но не упомянул, что в каждой пиале должно быть строго по одной гирьке. И если допускается в одну пиалу положить сразу две гирьки (и одна пиала останется свободной), требования соблюсти возможно, см. рис. 3.

Художник Алексей Вайнер

^* Мискаль — старинная азиатская мера веса (примерно 4,5 г).