Пространство треугольников (продолжение)

Алексей Панов, Дмитрий Ал. Панов, Пётр Панов
«Квантик» №2, 2021

Начало в «Квантике» №1, 2021.

Полюса и экваторы

Если продолжить аналогию с магнитными стрелками, то вершины R, G, B — конечно, полюса Треугольного Мира. И для них даже названия уже готовы — это Красный, Зелёный и Синий полюс.

На Земле синий конец магнитной стрелки указывает на Северный полюс, красный — на Южный. Понятно, что в Треугольном Мире вершины маленьких треугольников-стрелок должны быть маркированы цветом того полюса, на который они указывают.

Рис. 7

Теперь насчёт экватора. На Земле экватор — это линия, равноудалённая от Северного и Южного полюсов. На плоскости трудно представить себе линию, равноудалённую от трёх полюсов. Приходится признать, что в Треугольном Мире есть три экватора: на рисунке 7 это три серых отрезка, делящих треугольник RGB пополам. Каждый экватор равноудалён от своей пары полюсов и проходит через третий полюс. Экваторы пересекаются в центре Мира.

Меридианы

Если вы разобрались с упражнением 7, то знаете, каким свойством обладают треугольники, через которые проходят экваторы, — все они равнобедренные.

Это неплохой способ задавать некоторые линии, располагающиеся в Треугольном Мире. Нужно назвать какое-то свойство треугольника и посмотреть на карту Мира, например на ту, что на рисунке 7. Вдруг все треугольники, обладающие этим свойством, выстроятся в какую-то линию.

Рис. 8. Три линии, проходящие через прямоугольные треугольники

Это непростое упражнение, и мы сразу подскажем к нему ответ (рис. 8). Сверьте его с картой рисунка 7: действительно ли линии на рисунке 8 проходят среди треугольников с углами, близкими к 90°?

На рисунке 8 мы видим целых три линии, каждая проходит через свою пару полюсов. Нарисуем такие же линии для треугольников с углом 60° и для треугольников с углом 45° (рис. 9). Видно, что линии, соответствующие 60°, проходят через Центр Мира.

Рис. 9. Слева — линии, проходящие через треугольники с углом 60°, справа — через треугольники с углом 45°

Итак, каждая из линий на рисунках 8 и 9 соединяет два полюса нашего Мира и перпендикулярна экватору, соответствующему этим двум полюсам.

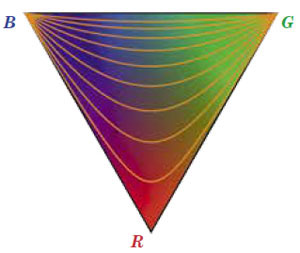
Рис. 10. Сеть меридианов, соединяющих Синий и Зелёный полюса

Но тем же условиям удовлетворяют и земные меридианы, соединяющие Северный и Южный полюса! Логично было бы объявить, что меридианы Треугольного Мира — это линии, которые соединяют два его полюса и проходят через треугольники, один из углов которых фиксирован.

На рисунке 10 — целая сеть меридианов, соединяющих Синий и Зелёный полюса и соответствующих треугольникам с углами от 15° до 135°, с шагом 15°. Две такие же сети меридианов соединяют другие пары полюсов.

А теперь ненадолго спустимся на Землю.

Карта мира Генриха Бюнтинга

Немецкий протестантский пастор, богослов и картограф Генрих Бюнтинг опубликовал в 1581 году книгу «Путешествие по святым местам», содержащую его знаменитую карту «Мир в форме трилистника клевера». Эта карта рисует Землю как гигантский Треугольный Мир из трёх континентов — Европы, Африки и Азии, раскрашенных в разные цвета и символизирующих Святую Троицу. Центр мира — Иерусалим. Гармония слегка нарушена недавно открытой Америкой и находящимися на периферии мира Англией и Данией. Карта Бюнтинга чем-то похожа на карту рисунка 9.

Мир в форме трилистника. Генрих Бюнтинг, 1581 год

Художник Мария Усеинова

Окончание в следующем номере.