Треугольник из кирпичей
Задача
На стройке лежала куча кирпичей красного, желтого и серого цвета. Бригадир строителей скомандовал своим рабочим выкладывать из них треугольную стенку по следующему правилу: для нижнего ряда взять из кучи 10 произвольных кирпичей, затем на соседние кирпичи одного цвета класть кирпич того же цвета, а на разноцветные — кирпич оставшегося цвета (пример такой пирамиды показан на рисунке).
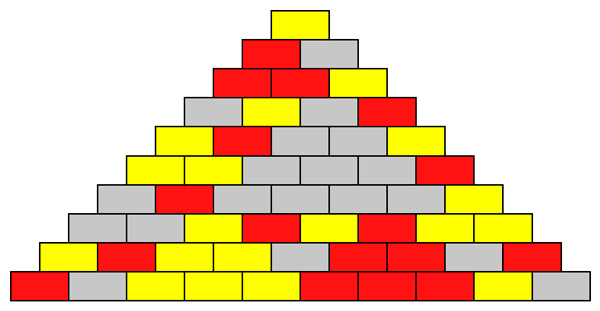
В итоге в верхнем ряду оказывается только один кирпич. Бригадир-математик, взглянув на кирпичи нижнего ряда, всегда быстро и точно угадывает, какого цвета будет верхний кирпич кладки. Как он это делает?
Подсказка 1
Зная нижний ряд, можно нарисовать картинку всех рядов этой кладки (и сделать это быстрее, чем строители успеют ее положить). Давайте отметём этот способ как нехарактерный для математика (и недостаточно быстрый).
Подсказка 2
Ясно, что конкретные цвета не важны. Вместо цветов можно использовать числа, например, 0, 1 и 2. Как тогда запишутся «правила добавления» нового кирпича? Понятно, что паре одинаковых чисел должно соответствовать такое же: (0, 0) → 0; (1, 1) → 1; (2, 2) → 2. Парам разных чисел соответствует третье: (0, 1) → 2 и так далее. Все эти соответствия можно выписать в одну табличку:
| 0 | 1 | 2 | |
| 0 | 0 | 2 | 1 |
| 1 | 2 | 1 | 0 |
| 2 | 1 | 0 | 2 |
А можно ли задать значения, приведенные в этой табличке, не таблично, а как-нибудь иначе? Можно попробовать. Например, единицы в таблице соответствуют парам (0, 2), (1, 1) и (2, 0) — тем, у которых сумма чисел равна 2. А двойки? Они соответствуют парам (0, 1), (1, 0) и (2, 2) — тем, в которых сумма равна либо 1, либо 4. Наконец, нули соответствуют парам (0, 0), (1, 2) и (2, 1) — тем, у которых сумма равна либо 0, либо 3. Это «либо» немножко путает: если бы его не было, например, если бы мы твёрдо знали, что сумме 3 соответствует 0, сумме 1 соответствует 2, а сумме 2 соответствует 1, то мы бы просто написали формулу соответствия: число3 = 3 − (число1 + число2). Из-за «либо» правило будет немного сложнее: если в результате число3 окажется не таким, как нужно, то к нему, возможно, придется добавить 3 или отнять от него 3. Но это не так уж существенно. Главное, что во всех случаях цвет следующего кирпича определяется суммой цветов тех кирпичей, которые стоят под ним. Подумайте, как бригадир мог это использовать.
Решение
Вместо формулы «число3 = 3 – (число1 + число2)», выведенной в Подсказке 2, мы будем использовать более простую: «число3 = – (число1 + число2)». Ведь всё равно к результату может быть нужно добавлять 3 или –3, так что ничего страшного, если мы это добавление/отнимание тройки не будем делать сразу же, а «отложим на потом».
Пусть в нижнем (10-м) ряду лежат кирпичи, которым соответствуют 10 чисел: a, b, c, d, e, f, g, h, i, j. Наша формула позволяет сразу же выписать весь вышележащий (9-й) ряд:
(ряд 9) –(a + b), –(b + c), –(c + d), –(d + e), –(e + f), –(f + g), –(g + h), –(h + i), –(i + j).
Но тогда и восьмой ряд тоже выписывается: над числами –(a + b) и –(b + c) должно быть записано число –(–a – b – b – c) = a + 2b + c. Таким образом, двойные минусы сократились, и восьмой ряд будет таким:
(ряд 8) a + 2b + c, b + 2c + d, c + 2d + e, d + 2e + f, e + 2f + g, f + 2g + h, g + 2h + i, h + 2i + j.
Считаем дальше. Числа седьмого ряда имеют вид –(a + 2b + c + b + 2c + d) = –(a + 3b + 3c + d). Вот здесь, пожалуй, пришло время вспомнить о том, что мы договорились откладывать все добавления и отнимания троек «на потом», и сделать это же самое со слагаемыми 3b и 3c, кратными 3. Таким образом, можно считать, что первое число седьмого ряда равно –(a + d). Тогда и весь ряд можно записать таким же образом:
(ряд 7) –(a + d), –(b + e), –(c + f), –(d + g), –(e + h), –(f + i), –(g + j).
Дальше у нас ряд 6, в котором снова сокращается двойной минус:
(ряд 6) a + b + d + e, b + c + e + f, c + d + f + g, d + e + g + h, e + f + h + i, f + g + i + j.
В ряде 5 минусы снова появляются (проследите за первым членом, а дальше всё аналогично):
(ряд 5) –(a + 2b + c + d + 2e + f), –(b + 2c + d + e + 2f + g), –(c + 2d + e + f + 2g + h), –(d + 2e + f + g + 2h + i), –(e + 2f + g + h + 2i + j).
В ряде 4 сокращаются и минусы, и куча слагаемых, при которых оказался коэффициент 3: вместо a + 3b + 3c + 2d + 3e + 3f + g мы оставим просто a + 2d + g:
(ряд 4) a + 2d + g, b + 2e + h, c + 2f + i, d + 2g + j.
Кирпичей, а с ними и вычислений, становится всё меньше:
(ряд 3) –(a + b + 2d + 2e + g + h), –(b + c + 2e + 2f + h + i), –(c + d + 2f + 2g + i + j);
(ряд 2) a + 2b + c + 2d + 4e + 2f + g + 2h + i, b + 2c + d + 2e + 4f + 2g + h + 2i + j.
И, наконец, кирпич в верхнем ряду:
(ряд 1) –(a + 3b + 3c + 3d + 6e + 6f + 3g + 3h + 3i + j) = –(a + j).
Что означает этот результат? Что цвет верхнего кирпича определяется суммой всего двух цветов из нижнего ряда — а именно, цветов двух крайних кирпичей. Причем определяется по тому же правилу, по которому строители кладут каждый следующий кирпич: двум одинаковым цветам соответствует такой же, а двум различным — оставшийся. Конечно же, бригадир-математик все эти вычисления и упрощения (вплоть до готового результата) проделал заранее, так что в момент постройки кирпичного треугольника сразу смотрел только на крайние кирпичи нижнего ряда.
Послесловие
Я специально постарался обойтись в решении самой примитивной алгеброй, чтобы сохранить у читателя ощущение «фокуса-покуса». Однако сейчас впору разобраться в существе этого фокуса немного глубже.
Во-первых, можно в каком-то смысле забыть про минусы: как мы видели, строчки с минусами и без них просто чередуются, так что мы с самого начала могли бы понять, что в верхней строчке минус будет.
Во-вторых, использованное нами сокращение троек (первый раз мы это сделали в восьмой строке), хотя и уменьшает вычисления, но затуманивает суть. Если бы мы этого не делали, то мы бы в седьмой строке увидели выражение вида a + 4b + 6c + 4d + e, в следующей — a + 5b + 10c + 10d + 5e + f, и так далее. Буквы в этих суммах идут по алфавиту, но что собой представляют последовательности чисел 1, 4, 6, 4, 1, потом 1, 5, 10, 10, 5, 1, потом 1, 6, 15, 20, 15, 6, 1? Любой мало-мальски сведущий в математике человек узнает в этих последовательностях строчки треугольника Паскаля:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
В этом треугольнике каждое число равно сумме двух чисел, стоящих на одну строчку выше: непосредственно над ним и соседнего с ним (слева). Собственно, появление здесь треугольника Паскаля не должно нас удивлять; например, число 15 — коэффициент при c в выражении a + 6b + 15c + 20d + ... — это сумма двух коэффициентов при с: один берется из выражения a + 5b + 10c + 10d + 5e + f, а другой — из выражения b + 5c + 10d + 10e + 5f + g. Иначе говоря, это сумма третьего (10) и второго (5) коэффициента из предыдущей строчки.
Таким образом, мы можем добраться и до нужной нам строчки. Коэффициенты в ней — 1 9 36 84 126 126 84 36 9 1. И поскольку все коэффициенты, кроме двух крайних единиц, делятся на 3, то это и дает нужный результат «фокуса».
Теперь можно попробовать сделать еще один естественный шаг и задать вопрос: а для каких значений длины нижнего ряда кирпичей (N) будет работать такой же фокус? Мы выяснили, что годится N = 10. Еще одно пригодное N = 4 (мы уже видели, что строчка 1 3 3 1 эквивалентна сумме двух крайних слагаемых). А еще какие значения годятся? Математический эквивалент этого вопроса звучит так: при каких N все коэффициенты (N – 1)-й строки треугольника Паскаля, кроме крайних, кратны 3? Этот вопрос значительно труднее нашей исходной задачки, но ответ на него тем не менее можно получить вполне элементарными математическими методами: N – 1 должно являться степенью тройки. Иначе говоря, следующее пригодное для фокуса N равно 28, потом 82, 244, 730 и т. д. Подробнее об этом, а также об обобщениях задачи на другое количество цветов, можно прочитать по-английски в статье Эрхарда Берендса и Стива Хамбла «Тайны треугольника» (“Triangle Mysteries”, PDF, 552 Кб), опубликованной во втором номере журнала The Mathematical Intelligencer за 2013 год (doi 10.1007/s00283-012-9346-4).
-
Небольшие опечатки:
вместо
> Но тогда и восьмой ряд тоже выписывается: над числами (–a + b)
должно быть
> Но тогда и восьмой ряд тоже выписывается: над числами –(a + b)
вместо
> Еще одно пригодное N – 4
должно быть
> Еще одно пригодное N = 4
т.е. вместо
-(a1+an) (mod 3)
будет
a1+2*am+an (mod 3)
, где a1, am и an - цвета первого, среднего и последнего кирпичей соответственно.
2: 1 1 (0)
3: 1 2 1 (2)
4: 1 0 0 1 (0)
5: 1 1 0 1 1 (2)
6: 1 2 1 1 2 1 (6)
7: 1 0 0 2 0 0 1 (2)
8: 1 1 0 2 2 0 1 1 (6)
9: 1 2 1 2 1 2 1 2 1 (11)
10: 1 0 0 0 0 0 0 0 0 1 (0)
11: 1 1 0 0 0 0 0 0 0 1 1 (2)
12: 1 2 1 0 0 0 0 0 0 1 2 1 (6)
13: 1 0 0 1 0 0 0 0 0 1 0 0 1 (2)
14: 1 1 0 1 1 0 0 0 0 1 1 0 1 1 (6)
15: 1 2 1 1 2 1 0 0 0 1 2 1 1 2 1 (14)
16: 1 0 0 2 0 0 1 0 0 1 0 0 2 0 0 1 (6)
17: 1 1 0 2 2 0 1 1 0 1 1 0 2 2 0 1 1 (14)
18: 1 2 1 2 1 2 1 2 1 1 2 1 2 1 2 1 2 1 (24)
19: 1 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 1 (2)
20: 1 1 0 0 0 0 0 0 0 2 2 0 0 0 0 0 0 0 1 1 (6)
21: 1 2 1 0 0 0 0 0 0 2 1 2 0 0 0 0 0 0 1 2 1 (11)
22: 1 0 0 1 0 0 0 0 0 2 0 0 2 0 0 0 0 0 1 0 0 1 (6)
23: 1 1 0 1 1 0 0 0 0 2 2 0 2 2 0 0 0 0 1 1 0 1 1 (14)
24: 1 2 1 1 2 1 0 0 0 2 1 2 2 1 2 0 0 0 1 2 1 1 2 1 (24)
25: 1 0 0 2 0 0 1 0 0 2 0 0 1 0 0 2 0 0 1 0 0 2 0 0 1 (11)
26: 1 1 0 2 2 0 1 1 0 2 2 0 1 1 0 2 2 0 1 1 0 2 2 0 1 1 (24)
27: 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 (38)
28: 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 (0)
29: 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 (2)
30: 1 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 1 (6)
31: 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 (2)
32: 1 1 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 1 (6)
33: 1 2 1 1 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 1 1 2 1 (14)
34: 1 0 0 2 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 2 0 0 1 (6)
35: 1 1 0 2 2 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 2 2 0 1 1 (14)
36: 1 2 1 2 1 2 1 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 1 2 1 2 1 2 1 (24)
37: 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 (2)
38: 1 1 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 1 1 (6)
39: 1 2 1 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0 1 2 1 (14)
40: 1 0 0 1 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 1 (6)
41: 1 1 0 1 1 0 0 0 0 1 1 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 1 0 0 0 0 1 1 0 1 1 (14)
42: 1 2 1 1 2 1 0 0 0 1 2 1 1 2 1 0 0 0 0 0 0 0 0 0 0 0 0 1 2 1 1 2 1 0 0 0 1 2 1 1 2 1 (30)
43: 1 0 0 2 0 0 1 0 0 1 0 0 2 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 2 0 0 1 0 0 1 0 0 2 0 0 1 (14)
44: 1 1 0 2 2 0 1 1 0 1 1 0 2 2 0 1 1 0 0 0 0 0 0 0 0 0 0 1 1 0 2 2 0 1 1 0 1 1 0 2 2 0 1 1 (30)
45: 1 2 1 2 1 2 1 2 1 1 2 1 2 1 2 1 2 1 0 0 0 0 0 0 0 0 0 1 2 1 2 1 2 1 2 1 1 2 1 2 1 2 1 2 1 (50)
46: 1 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 1 (6)
47: 1 1 0 0 0 0 0 0 0 2 2 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 2 2 0 0 0 0 0 0 0 1 1 (14)
48: 1 2 1 0 0 0 0 0 0 2 1 2 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0 1 2 1 0 0 0 0 0 0 2 1 2 0 0 0 0 0 0 1 2 1 (24)
49: 1 0 0 1 0 0 0 0 0 2 0 0 2 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 1 0 0 0 0 0 2 0 0 2 0 0 0 0 0 1 0 0 1 (14)
50: 1 1 0 1 1 0 0 0 0 2 2 0 2 2 0 0 0 0 1 1 0 1 1 0 0 0 0 1 1 0 1 1 0 0 0 0 2 2 0 2 2 0 0 0 0 1 1 0 1 1 (30)
51: 1 2 1 1 2 1 0 0 0 2 1 2 2 1 2 0 0 0 1 2 1 1 2 1 0 0 0 1 2 1 1 2 1 0 0 0 2 1 2 2 1 2 0 0 0 1 2 1 1 2 1 (50)
52: 1 0 0 2 0 0 1 0 0 2 0 0 1 0 0 2 0 0 1 0 0 2 0 0 1 0 0 1 0 0 2 0 0 1 0 0 2 0 0 1 0 0 2 0 0 1 0 0 2 0 0 1 (24)
53: 1 1 0 2 2 0 1 1 0 2 2 0 1 1 0 2 2 0 1 1 0 2 2 0 1 1 0 1 1 0 2 2 0 1 1 0 2 2 0 1 1 0 2 2 0 1 1 0 2 2 0 1 1 (50)
54: 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 (78)
55: 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 (2)
....
upd. А доказательство можно несложное придумать, не как для общего случая в буржуйской публикации, с кучей лемм.
Достаточно рассмотреть как формируется биномиальный коэффициент для n=3^t, обращая внимания на числа, делящиеся на 3, в числителе и знаменателе, например:
{27}*26*25*(24)*23*22*(21)*20*19
1 *2 *(3 )*4 *5 *(6 )*7 *8 *[9 ]
Преобразование задающее цвет верхнего кирпича таково: нужно к углу соответствующему цвету правого кирпича прибавить разницу углов между "правым" и "левым" цветом.
Так нагляднее получается.
Последние задачи














