Слова на ленте (окончание)

Виктор Клепцын
«Квантик» №6, 2020

Начало в № 5.

Напомним, что Квантик, Женя и Мика изучают бесконечное слово Фибоначчи ABAABABAABAAB..., которое получается из буквы A чередой замен, когда каждая буква A заменяется на AB, а каждая буква B на A. Возникающие после замен слова A, AB, ABA, ABAAB,... продолжают друг друга и все являются начальными участками слова Фибоначчи.

Тут Мика посмотрел на выписанное начало слова Фибоначчи и задумался:

— Интересно: на вид кажется, что буквы A и B в нём «размешаны» очень равномерно, причём букв A больше. А во сколько раз?

— Мы уже знаем, что количества букв A и B в каждом очередном начальном слове будут последовательными числами Фибоначчи, — отреагировала Женя. — Поэтому их отношение — это отношение двух последовательных чисел Фибоначчи.

— А такие отношения становятся с ростом номера всё ближе к известному ещё древним грекам золотому сечению \(φ\), — продолжил Квантик. — Не хотите попробовать угадать, чему оно должно быть равно?

— Пусть у нас есть какое-то слово, которое мы подаём на вход машине. Тогда в следующем слове букв B будет столько, сколько сейчас A, а букв A столько, сколько букв A и B вместе взятых. Если отношение почти не меняется, то должно быть такое правило: «букв A (примерно) во столько же раз больше, чем букв B, во сколько раз всех букв больше, чем букв A».

— Правильно; а ещё можно в таком отношении поделить отрезок — тогда отношение большей части к меньшей будет таким же, как всего отрезка к большей части; так золотое сечение и определяли древние греки. Кстати, в таком отношении диагональ правильного пятиугольника делит другую диагональ в точке их пересечения. (А ещё об этом можно почитать в прошлых номерах «Квантика»¹ и «Кванта»².)

Сделав паузу, Квантик продолжил:

— Ещё не очень сложно написать, какому уравнению золотое сечение \(φ\) удовлетворяет. Напишете?

— Если меньшую часть отрезка (или количество букв B) принять за единицу, то большая часть отрезка (количество букв A) будет равна \(φ\), а весь отрезок (или всё слово) будет ещё в \(φ\) раз больше и будет равняться \(φ^2\). Но отрезок есть сумма своих частей (а слово состоит из букв A и B) — и получается, что \(φ^2\) = \(φ\) + 1. Только как отсюда \(φ\) найти?

— Всё верно, — подтвердил Квантик. — Это квадратное уравнение, и вы ещё не умеете его решать. Но если я скажу ответ, то его не очень сложно подставить и проверить. А ответом будет \(φ = \frac{\sqrt{5} + 1}{2}\). Кстати, это число иррациональное; нельзя ли это к чему-нибудь применить?

— Мы собирались после разобраться, почему слово Фибоначчи не периодичное. Может быть, сюда? — догадалась Женя. — Если бы слово Фибоначчи было периодичным, оно состояло бы из повторений своего периода. И тогда число израсходованных букв A и B становилось бы всё ближе к их отношению за период. И это было бы рациональное число. А корень из 5 — и золотое сечение — числа иррациональные, их нельзя записать как отношение двух целых чисел! Вот поэтому слово Фибоначчи и не может быть периодичным.

Мика присмотрелся к красно-синим треугольникам на рисунке 2 прошлого номера и начал их считать.

— Так, — сказал он, — в треугольнике, который мы получили за две замены, 3 синих треугольника и 5 красных. В том, что получили за три замены, — 8 синих и 13 красных. Это же опять числа Фибоначчи!

— И если это так, а это наверняка так, — подхватила Женя, — то красных треугольников в большом-большом треугольнике опять примерно в \(φ\) раз больше, чем синих. И поэтому то же рассуждение утверждает, что и мозаика на плоскости не может быть периодичной!

— Молодцы, вы абсолютно правы, — подтвердил Квантик. — Ещё можно было бы сказать, что не бывает мозаик, одновременно периодических и сохраняющихся при повороте на 1/10 оборота, но это уже другая история.

— Интересно, — опять задумался Мика. — Вот мы знаем, сколько в начальной части слова Фибоначчи букв A и B, если длина этого начала — число Фибоначчи. А сколько каких букв попадут в первые сто? Или в первую тысячу? Ведь ни 100, ни 1000 не будут числами Фибоначчи.

— Давай посмотрим! — предложил Квантик. — Возьмём листочек в клеточку и для каждого начального участка отметим, сколько там букв A (их мы отложим по горизонтали), а сколько B (их мы отложим по вертикали). И ещё раскрасим точку с этими координатами тем же цветом, что и последняя буква участка.

Женя взялась за работу, и через какое-то время точки заняли свои места: у неё получилась картинка как на рисунке 4, слева.

Рис. 4. Количество букв A и B среди первых n букв слова Фибоначчи

— Ух ты, все точки попали в очень узкую полоску, — удивилась Женя. — То есть отношение количеств букв всегда очень-очень близко к золотому сечению!

— Именно так, — подтвердил Квантик.

— А ещё, — подхватил Мика, — кажется, в этой полосе все синие точки ближе к верхнему краю, а красные — к нижнему. Только это уже на глаз не очень надёжно проверять...

— И это правда, — поддержал его Квантик. — Давайте аккуратно спроецируем их все на перпендикуляр к оси этой полосы; смотрите, что получается!

Квантик добавил все проекции (на этот раз воспользовавшись компьютером, чтобы обеспечить нужную точность) — и оказалось, что проекции синих точек «заметают» один отрезок, а проекции красных — другой (рис. 4, справа).

— Забавно. А что будет, если брать другие правила замены? — поинтересовалась Женя.

— Вообще может получиться довольно много разного. Но самое красивое получается, если перестроить машину так, чтобы слова состояли уже из трёх букв, A, B и C, а машина обрабатывала бы их по правилам A → AB, B → AC, C → A.

— Тогда, — продолжил Квантик, — начав с буквы A и применяя новую машину снова и снова, можно получить новое бесконечное слово. Его в шутку называют словом Трибоначчи, хотя математика Трибоначчи, конечно, никогда не существовало:

— Интересно! — отреагировал Мика. — А тут в каком соотношении разделятся используемые буквы?

— Тут тоже отношения количеств букв A к B и B к C становятся всё ближе и ближе к некоторому числу x = 1,839..., которое уже задаётся кубическим уравнением x³ = x² + x + 1. А если отложить количества этих букв по трём осям, то получится красивая пространственная «змейка», ползущая в одном конкретном направлении. И, как и раньше, от этого направления она не сильно уклоняется.

Квантик нажал на несколько кнопок — и на экране появилась картинка как на рисунке 5, слева.

— Но самое интересное будет, если раскрашенные в три цвета (по последней букве слова) точки спроецировать на правильно выбранную плоскость.

Тут Квантик нажал ещё несколько кнопок, и на экране возникла проекция: сначала она состояла из отдельных точек, а потом их стало настолько много, что они слились в фигуры (рис. 5, в центре и справа). А Квантик продолжил объяснять:

— Если для слова Фибоначчи мы видели два отрезка, то тут вся проекция разрезается на три непересекающиеся части. И оказывается, все они, и фигура целиком, и каждая из частей, подобны друг другу, причём с поворотом! А площади у частей относятся именно как 1 : x : x². Эта замечательная фигура называется фракталом Рози.

Рис. 5. Количество букв A, B и C среди первых n букв слова Трибоначчи и появление фрактала Рози

Кстати, большую из частей можно опять подразбить на три, подобные ей. А потом подразбить и большие из имеющихся частей, и повторить это несколько раз. Если потом увеличить самую большую из оставшихся частей до исходного размера, получается разбиение всё большей и большей области на плоскости — а в пределе и (непериодичное!) разбиение всей плоскости. Кстати, фрактал Рози возникает и в совсем современных математических статьях (рис. 6).

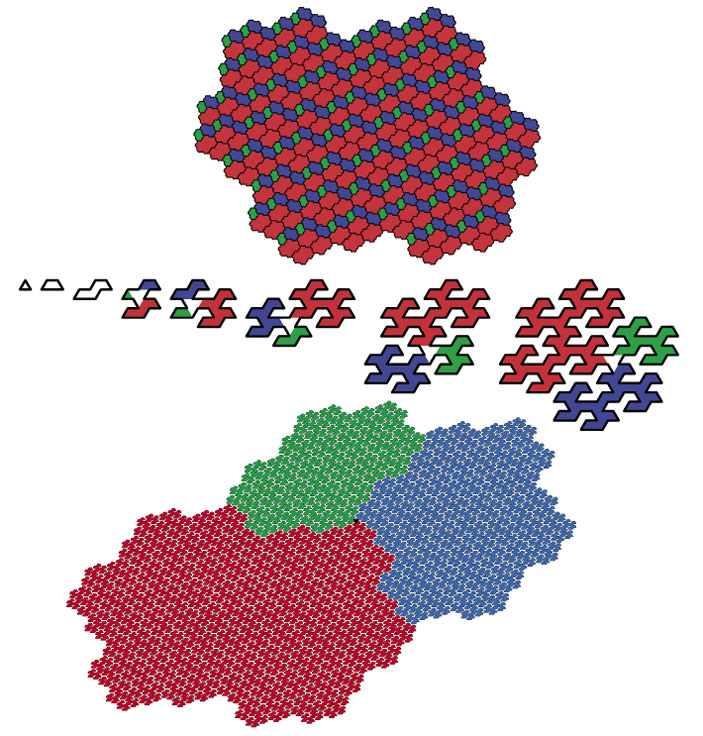
Рис. 6. Сверху — квазипериодичное разбиение плоскости, снизу — появление фрактала Рози в статье W. P. Hooper, B. Weiss «Rel leaves of the Arnoux-Yoccoz surfaces» (Selecta Mathematica, 2018)

Художник Мария Усеинова

P.S. Автор благодарит О. Ромаскевич, Г. Мерзона и А. П. Веселова, без них этой статьи бы не было. Интересные материалы о «хорошо перемешанных» последовательностях букв, подстановочных словах, фрактале Рози см. по ссылке.

¹ Александра Подгайц. Интересные факты о золотом сечении // Квантик. 2013, № 6.

² А. Спивак. Числа Фибоначчи // Квант. 2003, № 2.