Слова на ленте
Виктор Клепцын
«Квантик» №5, 2020

Зайдя в гости к Квантику, Женя и Мика обнаружили у него на столе странное устройство. На его ленте было напечатано ABAAB.
— А что эта машина делает? — спросил Мика.
— Она читает одну ленту и печатает другую, — начал объяснять Квантик. — Каждый раз, встретив на входной ленте букву A, на выходной ленте машина печатает AB, а встретив на входной ленте букву B, машина печатает A. Вот смотрите!
Квантик взял ленту со словом ABAAB и перенёс её к считывающей части машины. Машина загудела, потянула ленту и напечатала ABAABABA.
— Я начал с самого простого слова, буквы A, — продолжил Квантик. — Из него машина сделала AB, а из него ABA; потом ABAAB, а дальше вы видели.
— А что вообще можно про эти слова сказать? — задумалась Женя и переписала их на доску.
— Ага! Каждое новое слово всегда продолжает предыдущее! — заметила она.
— Верно! А доказать сможете? — спросил Квантик.
— Давай с примера начнём, — вмешался практичный Мика. — Вот слово ABA начинается со слова AB. Следующее за ним слово, ABAAB, получается, если машина читает ABA. Но при этом сначала она прочтёт AB и напечатает как раз ABA.
— Точно! Так будет и дальше, — поддержала Женя. — Пусть мы уже знаем, что n-е слово продолжает предыдущее, (n − 1)-е. Чтобы получить (n + 1)-е слово, мы подаём на вход n-е слово. Машина сначала прочтёт его первую часть, то есть (n − 1)-е слово. И, читая его, по определению напечатает n-е слово, с которого (n + 1)-е слово и начнётся.
— Правильно, — подтвердил Квантик. — Такое рассуждение, когда каждое утверждение выводится из предыдущего, образуя этакую «цепочку вывода», называется математической индукцией. Ещё для неё нужно проверить базу: самое-самое первое утверждение, чтобы цепочке было откуда начинаться. Но раз вы уже знаете, что второе слово, AB, начинается с первого, A, то так будет и дальше: третье будет начинаться со второго, четвёртое с третьего и т.д. — каждое следующее будет продолжать предыдущее.
Сделав паузу, Квантик продолжил:
— А что ещё об этих словах можно сказать?
— Первое, что приходит в голову, это посмотреть на длины этих слов, — предложила Женя. — Они становятся всё длиннее. Можно посмотреть, как именно.
После недолгих подсчётов на доске появилась таблица:
| Слово | Длина |
|---|---|
| A | 1 |
| AB | 2 |
| ABA | 3 |
| ABAAB | 5 |
| ABAABABA | 8 |
| ABAABABAABAAB | 13 |

— Это же знаменитая последовательность Фибоначчи! — сказала Женя. — Она начинается с двух единиц, а каждое следующее число — сумма двух предыдущих.
Мика на всякий случай записал начало последовательности Фибоначчи на другой половине доски:
1, 1, 2, 3, 5, 8, 13 = 8 + 5, ...
— Точно! Но она тут со сдвигом: длина n-го слова — это (n + 1)-е число Фибоначчи, — подтвердил он. — Только вот как это доказать?
— Хороший вопрос, — задумалась Женя. — Давай посмотрим, как будут расти длины наших слов. Когда машина читает очередное слово, то из каждой буквы A получается две буквы нового слова, а из каждой буквы B только одна. Но проблема в том, что мы не знаем, сколько в слове букв A и B по отдельности!
— Ну, если не знаем, то почему бы нам это не узнать? — с энтузиазмом ответил Мика. — Давай подсчитаем, сколько в каких словах каких букв!
В таблице на доске появились два новых столбца, NA и NB, для количеств букв A и B соответственно — и ещё одна строчка: машина как раз только что закончила печатать слово ABAABABAABAAB:
| Слово | Длина | NA | NB |
|---|---|---|---|
| A | 1 | 1 | 0 |
| AB | 2 | 1 | 1 |
| ABA | 3 | 2 | 1 |
| ABAAB | 5 | 3 | 2 |
| ABAABABA | 8 | 5 | 3 |
| ABAABABAABAAB | 13 | 8 | 5 |
— Так это те же последовательности, только со сдвигом! — заметила Женя. — Ну конечно! Ведь из каждой буквы предыдущего слова всегда получается ровно одна буква A. Поэтому букв A в новом слове всегда столько же, какова длина предыдущего слова.

— А буква B получается только из буквы A, — подхватил Мика. — Значит, в новом слове их столько, сколько букв A в предыдущем, то есть какова длина пред-предыдущего!
— Но тогда у нас всё получается! — обрадовалась Женя. — В новом слове столько букв A, какова длина предыдущего, и столько букв B, какова длина предпредыдущего. Значит, его длина — это сумма этих длин, и это в точности соотношение, задающее последовательность Фибоначчи. Так что если их длины были числами Фибоначчи, то и длина нового слова будет следующим числом Фибоначчи.
— Верно, — подтвердил Квантик. — И вы опять применили индукцию! Правда, поскольку вы используете два предыдущих утверждения, нужно проверить два первых утверждения «цепочки». Но мы уже знаем, что первые два слова (A и AB) имеют длины 1 и 2, и это нужные нам числа Фибоначчи.
— А ещё что-нибудь красивое можно про эти слова сказать? — с интересом спросил Мика.
— Конечно! — ответил Квантик. — Вы уже заметили, что следующее слово продолжает предыдущее. А что идёт в следующем слове за этим предыдущим?
— Посмотрим! — взяла мел Женя. — Вот у нас слово ABAABABAABAAB; отделяем ABAABABA, остаётся...

— Да это же пред-предыдущее слово! — удивилась она. — То есть нашу последовательность слов можно ещё определить так: каждое новое слово в ней — это предыдущее, за которым идёт пред-предыдущее.
— Правильно! А как это доказать?
— Как и раньше, по индукции! — ответила Женя. — Ведь если мы знаем, что n-е слово — это (n − 1)-е, за которым идёт (n − 2)-е, и подаём его на вход машине, то получим по определению (n + 1)-е слово. Но сначала машина (читая (n − 1)-е) напечатает n-e, а потом (читая (n − 2)-е) напечатает (n − 1)-е.
— Молодец, — похвалил Квантик. — И заметьте: раз все слова продолжают друг друга, есть некое бесконечное слово, началами которого они все являются:
ABAABABAABAABABAABABAABAABABAABAAB...

Это слово называется словом Фибоначчи. А что будет, если написать его на бесконечной ленте (допустим, у нас есть пара таких) и подать машине на вход?
— Сейчас... — задумалась Женя. — Прочтя A, машина напечатает AB; прочтя AB, напечатает ABA... Ой, да ведь она напечатает это же самое слово!
— Именно так. Кстати, слово Фибоначчи — единственное слово с таким свойством. Можешь разобраться почему? — продолжил спрашивать Квантик.
— Если подать на вход слово, начинающееся с B, то вывод будет начинаться всё равно с A, и слово на выходе будет другим, — продолжила рассуждать вслух Женя. — Значит, слово должно начинаться с A. Но тогда машина, прочитав эту букву, напечатает AB, значит, слово начинается с AB. А значит, и с ABA, которое машина напечатает, прочтя AB, и так далее; да это же почти то же самое рассуждение!
— Всё правильно, — подтвердил Квантик. — Кстати, слово Фибоначчи обладает и другими замечательными свойствами. Например, оно не периодично, и мы ещё увидим почему. Но оно квазипериодично: любой кусочек, который встречается в нём хоть где-нибудь, встречается регулярно.
— А почему? — заинтересовалась Женя.

— Начнём с простого: можете ли вы что-нибудь сказать про то, как часто встречается буква A?
— В тех словах, что мы уже выписали, ни разу даже двух букв B подряд не было, — отметил Мика.
— Очень хорошо, а как это доказать?
— Надо чем-нибудь воспользоваться... — задумалась Женя. — Мы знаем, что машина по слову Фибоначчи печатает его же. Но буква B может появиться, только если машина прочитала букву A и напечатала AB. Значит, перед любой буквой B идёт буква A!
— Замечательно; а что, если мы спросим про слово AB? — усложнил задачу Квантик.
— Машина печатает его, прочитав букву A, — уверенно ответил Мика. — Но из любых двух соседних букв хотя бы одна — это A. Значит, можно разрезать слово Фибоначчи на кусочки AB и A, и из двух последовательных кусочков хотя бы один будет нужным.
— Правильно. Или можно применить машину ещё раз, и тогда всё слово Фибоначчи разрежется на кусочки ABA и AB, в каждом из которых есть нужное нам подслово, — согласился Квантик. — А что, если мы ищем кусочек AAB?

— Давай его найдём где-нибудь. Вот он, в слове ABAAB, — сориентировалась Женя. — Но если мы ещё несколько раз применим нашу машину, слово Фибоначчи разрежется на слова ABAABABA и ABAAB, и в каждом из них нужный нам кусочек есть. Ой, а ведь это рассуждение и в других случаях сработает?
— Да, — подтвердил Квантик. — Любое подслово X, которое где-нибудь в слове Фибоначчи встречается, содержится в одном из тех слов, которые получаются из буквы A чередой прогонов через нашу машину. И всё слово Фибоначчи разрезается на его копии и копии следующего за ним слова. Но раз следующее слово начинается с предыдущего — то в каждом из таких кусочков встречается слово X. Вот мы всё и доказали!
— Кстати, — продолжил Квантик, — аналог такого слова есть и в геометрии, в замощениях плоскости. Возьмём правильный пятиугольник ABCDE и проведём в нём диагонали AC, BD и CE. Треугольники, которые в результате образуются, обладают похожим замечательным свойством: из красного и синего треугольников можно сложить больший треугольник, подобный синему, а из двух красных и синего (или, что то же самое, добавив ещё один меньший красный к большему синему) — больший, подобный красному.
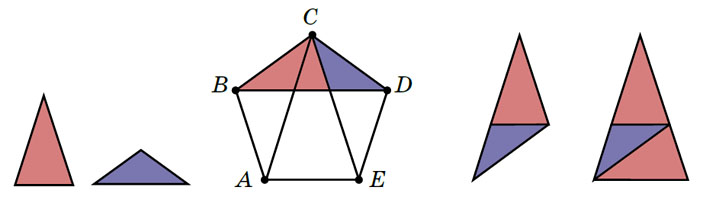
Квантик нарисовал соответствующую картинку (рис. 1), и Женя подхватила:
— А дальше мы можем продолжить? Собрать из этих треугольников ещё большие треугольники?
— Можем, — подтвердил Квантик. — Кстати, это всё равно, что разбить каждый красный и синий треугольники на более мелкие, а потом увеличить всю картинку. И если повторить такую замену много-много раз, то получится квазипериодичное разбиение угла в 36° на красные и синие треугольники (рис. 2). А если объединить 10 таких углов, то и всей плоскости!

Рис. 2. Красный треугольник после двух, трёх и пяти замен
Сделав паузу, Квантик продолжил:
— Квазипериодические мозаики были известны с 1960-х годов, в 1970-х появились похожие на это разбиение мозаики Пенроуза (рис. 3). А в 1982 году Дан Шехтман открыл устроенные подобным образом вещества — квазикристаллы, — что в 2011-м принесло ему Нобелевскую премию по химии!

Рис. 3. Мозаики Пенроуза. Автор: Inductiveload, Викисклад
Художник Мария Усеинова
Окончание в следующем номере.


























Рис. 1. Слева: красный и синий треугольники по отдельности. В центре: их появление в правильном пятиугольнике. Справа: сложенные из них подобные им большие треугольники