Как мы собирали абажур, или Приключения триаконтаэдра (окончание)
Алексей Панов, Пётр Панов
«Квантик» №9, 2019
Начало см. в «Квантике» № 7 и № 8 за 2019 год.
Апериодические мозаики Роджера Пенроуза

Математики оказались более подготовленными. Ещё в 1960-е годы они тоже обнаружили и начали изучать новые необычные объекты — апериодические мозаики. Вообще мозаики — это узоры из многоугольных плиток, целиком заполняющих плоскость. Апериодические мозаики — это те, которые не самосовмещаются ни при каком сдвиге, то есть ни при каком параллельном переносе.
Самые известные из апериодических мозаик — это мозаики Пенроуза. Фрагмент такой мозаики изображён на рисунке 22. Она собирается по определённым правилам из нескольких типов многоугольников и заполняет всю плоскость.
Её часто сравнивают с рисунком Кеплера из Harmonices Mundi (рис. 23), о котором сам Пенроуз говорит так: «Он пытался сделать что-то близкое к тому, что сделал я, но у него это не совсем получилось».
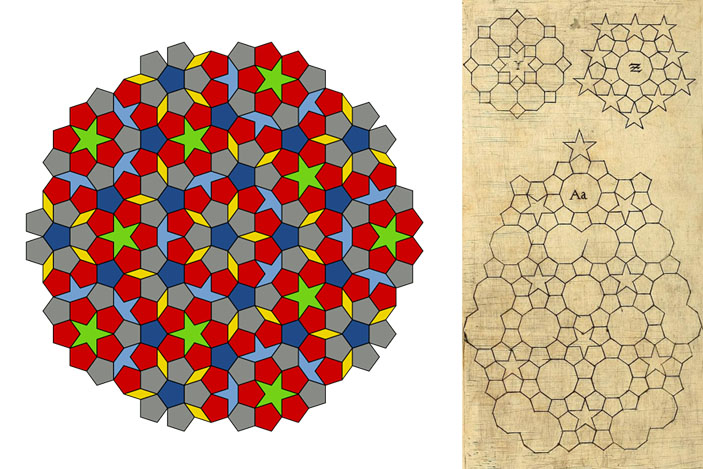
Рис. 22 (слева). Фрагмент мозаики Пенроуза. Рис. 23. Рисунок из Harmonices Mundi
Мы чуть подробней обсудим другой тип апериодических мозаик Пенроуза.
Они составляются из двух видов ромбов — тонких с острым углом 36° и толстых с острым углом 72°. Одна из них изображена на рисунке 24. Она, конечно, не такая симметричная, как те, что на рисунке 18 в статье из прошлого номера, — не совмещается с собой ни при каком параллельном переносе, и у неё нет осей симметрии. Тем не менее, видны повторяющиеся пятиугольные звёзды, каждая из них совмещается с собой при повороте на 72° = 360°/5. Кроме того, эти звёзды разбиваются на два класса (рис. 25), и звёзды одного класса отличаются от звёзд другого класса поворотом на 36° = 360°/10.

Рис. 24. Мозаика из ромбов с острыми углами 36° и 72°
Верен более общий факт. Каждая область, состоящая из конечного числа параллелограммов, повторяется в мозаике бесконечное число раз, и повёрнутая на 36° она тоже встретится бесконечное число раз.

Рис. 25. Разноцветные звёзды отличаются поворотом на 36°
Теперь несколько слов о физических свойствах мозаики Пенроуза.
Алан Маккей: дифракция на мозаике

Алан Маккей. Фото: Julyan-cartwright, Wikimedia Commons; CC-BY-SA-3.0
Алан Маккей предложил применить стандартную физическую процедуру для нестандартного математического объекта — мозаики Пенроуза. Каждая вершина мозаики была заменена маленьким кружком, полученная точечная картина была уменьшена — сжата до таких размеров, чтобы расстояния между кружками-точками стали соизмеримыми с длиной световой волны. Эта миниатюра была просвечена лазером, и оказалось, что полученная дифракционная картина, как и в эксперименте Шехтмана, обладает осью симметрии десятого порядка. Работа Маккея была опубликована в том же 1982 году, когда Шехтман проводил свой первый эксперимент.
Если бы Шехтман знал об этой работе Маккея, то мог бы сослаться на неё и добиться скорейшего признания своих достижений. Но Шехтман говорит, что в то время он не был осведомлён о результатах Маккея.
Возвращение триаконтаэдра и появление гексаконтаэдра

Роджер Пенроуз и Роберт Амманн. Фото: Ludwig Danzer; из статьи Marjorie Senechal «The Mysterious Mr. Ammann»
Существуют трёхмерные аналоги апериодических мозаик Пенроуза. Один такой тип мозаик был открыт Робертом Амманном. Они собираются из двух видов ромбических параллелепипедов, как раз тех самых, что изображены в нижней части рисунка 16 в статье из прошлого номера — вытянутого и сплюснутого.
Точно так же, как на плоских мозаиках Пенроуза часто встречаются пятиугольные звёзды (рис. 24 и 25), в апериодических пространственных мозаиках Амманна часто встречаются ромбические триаконтаэдры, а также шестидесятигранные ромбические гексаконтаэдры. Гексаконтаэдр отсутствовал в нашем списке ромбических многогранников, но это потому, что он невыпуклый — у него 12 впадин (рис. 26).

Рис. 26. Гексаконтаэдр, собранный из золотых ромбов
Впоследствии физикам удалось обнаружить реальные квазикристаллы, имеющие формы триаконтаэдра и гексаконтаэдра.
И вот под конец ещё несколько упражнений на тему гексаконтаэдра и мозаики Пенроуза.
- Из 60 золотых ромбов соберите гексаконтаэдр. Также проверьте, что и триаконтаэдр, и ромбический икосаэдр Фёдорова аккуратно вкладываются во все 12 полостей этого гексаконтаэдра (см. трёхмерные модели этих тел).
- Мы говорили о том, что триаконтаэдры и гексаконтаэдры часто встречаются в мозаиках Амманна. Проверьте, что на самом деле гексаконтаэдр можно составить из 20 вытянутых параллелепипедов, а триаконтаэдр — из 10 вытянутых и 10 сплюснутых параллелепипедов.
- Доказано, что в достаточно большом куске мозаики Пенроуза отношение числа толстых ромбов к числу тонких близко к золотому сечению φ = 1,618... Используя рисунок 24, проверьте это утверждение.
- Мозаика Пенроуза, как и все наши многогранники, состоит из ромбов, поэтому у неё тоже имеются зоны. На этот раз зона представляет собой бесконечную цепочку ромбов. Каждый ромб имеет с двумя соседними по общей стороне, и эти стороны параллельны. На нашем сайте можно найти картинку мозаики Пенроуза. Раскрасьте на ней несколько зон, посмотрите, как они могут быть расположены друг относительно друга.
Ответ
К решению последнего упражнения:

Дополнительные материалы к статье.
Заключение

Кеплер был устремлён в будущее. По общему мнению, самая выдающаяся работа Кеплера — это его открытие трёх законов движения планет. Ньютон узнал о них ещё во время своей учёбы в Тринити-колледже, и через несколько десятилетий использовал их при разработке своей теории тяготения.
Сам же Кеплер считал своим высшим достижением разгадку геометрического устройства Вселенной. На протяжении всей своей жизни он разрабатывал её многогранно-сферическую модель.
А триаконтаэдр Кеплера теперь — один из символов современной кристаллографии.
Художник Анна Горлач






















Роджер Пенроуз. Фото: Biswarup Ganguly, Wikimedia Commons; CC-BA-3.0