Как мы собирали абажур, или Приключения триаконтаэдра
Алексей Панов, Пётр Панов
«Квантик» №7, 2019

После ремонта мы решили поменять все светильники и купили новый абажур, который называется IQ-light. Он весит всего 100 граммов. Такой лёгкий он потому, что собирается из 30 тонких гибких пластинок. Каждая пластинка имеет четырёхугольную форму и снабжена четырьмя крючками. Эту конструкцию придумал в 1973 году датский дизайнер Хольгер Стрём.
Буквы IQ в названии означают Interlocking Quadrilaterals — сцепленные четырёхугольники. На рисунке 1 видно, что в некоторых местах они сцепляются по пять штук, а в некоторых по три. Сама конструкция кажется сначала достаточно сложной, но, к счастью, к ней прилагается подробная инструкция, да и в процессе самой сборки становится понятным, что тут к чему.
Видно, что абажур представляет собой многогранник с одинаковыми гранями-ромбами (рис. 2).

Рис. 2. Ещё не полностью собранный абажур. Видно, что он составлен из ромбов
Установим его точное научное название. Начнём с таблицы числовых греческих префиксов, попросту — приставок.
Предмет со многими гранями можно назвать многогранником, а можно посмотреть в нижнюю строку таблицы, где в первом столбце стоит слово много, из второго столбца нужно взять приставку поли- и присоединить к ней слово эдр из третьего столбца, получится полиэдр. Тот же многогранник, но короче и звучит красиво.
Таблица греческих числовых префиксов
| Число | Префикс | Грань |
|---|---|---|
| 1 | моно | эдр |
| 2 | ди | |
| 3 | три | |
| 4 | тетра | |
| 6 | гекса | |
| 8 | окта | |
| 12 | додека | |
| 20 | икоса | |
| 30 | триаконта | |
| 60 | гексаконта | |
| много | поли |
Что касается нашего абажура, то у него 30 граней, и с помощью таблицы мы определяем его научное название — триаконтаэдр. Для надёжности можно добавить ещё одно слово и сказать ромбический триаконтаэдр. Именно так называет его Иоганн Кеплер в своей знаменитой книге Harmonices Mundi — «Гармония мира» (опубликована в 1619 году).
Желающим предлагаем пройтись по строкам таблицы и посмотреть, какие тут получаются названия. Может, встретите что-нибудь знакомое, а может, наоборот, удивитесь чему-нибудь неожиданному.
Иоганн Кеплер (1571–1630)

Начнём с картинки — небольшого отрывка из Harmonices Mundi (рис. 3). Справа там как раз изображён триаконтаэдр. Из 30 составляющих его ромбов нам видны только 10. Во второй строке текста на рисунке узнаётся название ромбического триаконтаэдра.
У другого, меньшего многогранника, всего 12 граней, и в соответствии с нашей таблицей он называется ромбическим додекаэдром.
Обратим внимание ещё на одно слово — Zona, оно расположено в предпоследней строке и относится уже к другому рисунку Кеплера, где изображён процесс сборки триаконтаэдра (рис. 4).

Рис. 3. Отрывок из Harmonices Mundi
Кеплер предлагает сначала собрать из ромбов пятиугольную звезду, дополнить её ещё пятью ромбами до, мы бы сказали, тарелки или чаши, но Кеплер сравнивает это со створкой раковины, а потом собрать ещё одну такую конструкцию. На рисунке они расположены друг против друга слева и справа. А между ними — как раз зона, состоящая из десяти ромбов. Заметьте, что все 10 отрезков, по которым соединены эти ромбы, параллельны друг другу. Теперь остаётся скрепить раковины с зоной, и сборка триаконтаэдра будет завершена.

Рис. 4. Сборка триаконтаэдра
У Кеплера имеется аналогичное графическое руководство и для сборки ромбического додекаэдра (рис. 5).

Рис. 5. Сборка ромбического додекаэдра
Дальше нас ждут некоторые эксперименты с этими многогранниками. Поэтому скоро мы соберём их, следуя как раз инструкциям Кеплера.
Все математики безоговорочно признают приоритет Кеплера в открытии ромбического триаконтаэдра, и это, безусловно, справедливо. Но есть два обстоятельства, о которых нужно сказать. Во-первых, у Кеплера были предшественники и, во-вторых, Кеплер не сказал, какие именно ромбы годятся для изготовления додекаэдра, а какие — для триаконтаэдра.
Венцель Ямницер (1508–1585)

Ямницер был одним из самых известных ювелиров своего времени — золотых дел мастером, художником, гравёром. Он работал в Нюрнберге, заведовал там монетным двором, а также был придворным ювелиром немецких императоров и проводил научные исследования, связанные со своей профессией. В 1568 году он опубликовал книгу под названием Perspectiva Corporum Regularium, которое можно перевести как «Вариации на тему правильных многогранников». Эта книга была собранием множества замечательных гравюр. И вот одна из них (рис. 6), и, конечно же, на ней изображён тот же самый триаконтаэдр, что у Кеплера в его Harmonices Mundi, только представленный рёбрами, а не гранями.
О подходящих ромбах

Рис. 6. Триаконтаэдр Венцеля Ямницера
Кеплер не написал, из каких ромбов можно собрать додекаэдр и из каких — триаконтаэдр. Это важный вопрос, а ответ на него таков: додекаэдр можно собрать из 12 равных ромбов с отношением диагоналей , а триаконтаэдр собирается из 30 равных ромбов с отношением диагоналей и только (что такое , сейчас объясним).
Число — это такое число, квадрат которого равен 2 и которое с хорошей точностью вычисляется одним нажатием кнопки на любом калькуляторе, а число называется золотым сечением, оно задаётся формулой и тоже легко вычисляется на калькуляторе: ,
При сборке многогранников нам такая точность не понадобится, и мы ограничимся приближениями , .
Добавим, что ромб, расположенный на рисунке 7 справа, называется золотым ромбом.

Рис. 7. Подходящие ромбы: из левых собирается ромбический додекаэдр, а из правых — триаконтаэдр
Как собирать триаконтаэдр

Рис. 8. Лист ватмана разбит на 50 ромбов с диагоналями 10 и 16 см
На рисунках Кеплера видно, какую сторону одного ромба с какой стороной другого нужно скреплять при сборке триаконтаэдра, но сам механизм соединения не указан. К счастью, у нас уже есть опыт сборки многогранников — смотрите статью «Бумажная модель плоскости Лобачевского» в журналах «Квантик» № 5 и 6 за 2018 год. Метод сборки, который мы там использовали, был изобретён американским архитектором Фредом Бассетти.
Прежде всего нам понадобится большой лист ватмана размером 61 × 86 см (формат А1) и большое количество резинок для купюр (их ещё называют банковскими или канцелярскими) диаметром 30 мм. Начнём с золотых ромбов — заготовок для граней триаконтаэдра. Обрежем лист ватмана до размеров 60 × 80 см и разметим его на ромбы с диагоналями 10 и 16 см, как показано на рисунке 8.
Вырежем все получившиеся 50 ромбов и один из них превратим в шаблон: вдоль границы ромба прямыми, параллельными его сторонам, отделим полоски шириной в 1 см (рис. 9).
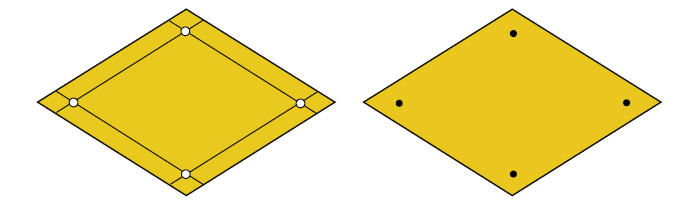
Рис. 9. Шаблон и размеченная с его помощью заготовка
Для нас важны точки попарного пересечения вспомогательных прямых, параллельных сторонам ромба. Там нужно сделать маленькие дырочки, через которые будут размечаться все остальные ромбы — заготовки для граней. После разметки нам предстоит продолжительная работа с ножницами и бумагой, основные этапы которой изображены на рисунке 10.
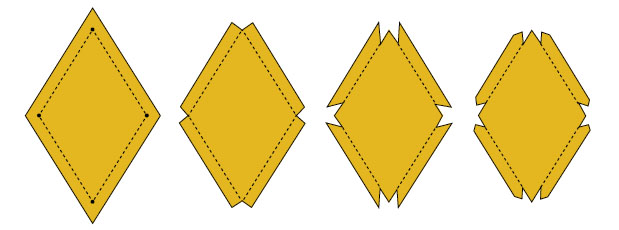
Рис. 10. Обработка заготовки

Рис. 11. Соединение граней
Слева на нём изображён размеченный ромб с дополнительными штриховыми линиями, по которым будут производиться сгибы. Эти линии рисовать не нужно, но полезно о них помнить. Сначала в каждой из вершин ромба, ориентируясь на отмеченную точку, вырежем по маленькому четырёхугольнику, а потом отогнём боковые полоски. Внутренний ромб окажется окружённым четырьмя полосками шириной 1 см и длиной, равной стороне внутреннего ромба. Дальше отрежем от каждой из этих полосок по паре маленьких треугольничков, а потом и ещё по два поменьше (рис. 10, справа).
На рисунке 11 мы видим уже готовые бумажные грани триаконтаэдра. Там же показан механизм соединения этих деталей-граней — они прикладываются друг к другу отогнутыми рёбрами, на которые накидывается слегка растянутая резинка.
Теперь самое время воспользоваться инструкцией Кеплера по сборке триаконтаэдра — рисунком 4. Его изготовление займёт у вас не больше 10 минут (рис. 12).
О сборке ромбического додекаэдра

Принцип сборки ромбического додекаэдра (рис. 13) тот же самый. Поскольку граней у него всего двенадцать, лист ватмана можно взять поменьше, а именно 42 × 59 см (формат А2). Его нужно обрезать до размера 40 × 56 см, отрезав по краям узенькие полоски шириной 2 и 3 см, а потом, наподобие рисунка 8, разбить его на 25 ромбов с диагоналями 10 и 14 см. Из одного полученного ромба нужно будет сделать шаблон с четырьмя дырками, разметить 12 ромбов, как на рисунке 9, обрезать их, как на рисунке 10, а потом с помощью тех же самых резинок собрать ромбический додекаэдр, используя рисунок 5.
Продолжение следует.
Художник Анна Горлач





















Рис. 1. Абажур IQ-light собирается из 30 четырёхугольников с крючками