Бумажная модель плоскости Лобачевского
Алексей Панов, Дмитрий Панов
«Квантик» №5 и №6, 2018
В 1978 году Ю. В. Матиясевич опубликовал в журнале «Квант»* статью под названием «Модели многогранников». В ней было рассказано о конструкторе для сборки многогранников, придуманном американским архитектором Фредом Бассетти. С помощью этого конструктора мы познакомимся с плоскостью Лобачевского, собрав её бумажную модель.
Добавим, что Фред Бассетти (1917–2013) — известный американский архитектор, по его проектам построено много красивых зданий. Свой конструктор он запатентовал в 1961 году, и впоследствии этот конструктор продавался под названием Flexagons.
Изготовление конструктора

В состав конструктора входят два типа деталей — резиновые колечки и многоугольные грани. В качестве колечек мы рекомендуем банковские резинки диаметром 4 см. Заготовки для граней вырезаются из листа ватмана — плотной белой бумаги. Мы будем собирать многогранники только из правильных треугольных граней, так что лист ватмана нужно разметить на правильные треугольники со стороной 12,5 см и нарезать их в большом количестве (рис. 1).
Один из полученных треугольников превратим в шаблон, проделав в нём три дырочки в точках пересечения трёх прямых, удалённых от сторон треугольника на 1 см (рис. 2). Далее карандашом размечаем все остальные треугольники, расставляя в каждом по три точки через дырки в шаблоне.

Рис. 2. Шаблон с тремя дырочками, ширина полосок в нём равна 1 см; справа — размеченный треугольник со сторонами 12,5 см
Теперь берём в руки ножницы и начинаем вырезать заготовки граней. Сначала в каждой из вершин треугольника, ориентируясь на отмеченную точку, вырежем по маленькому четырёхугольнику (рис. 3, слева), а потом отогнём боковые полоски вверх и хорошо прогладим сгибы. Дальше отрежем ещё шесть маленьких треугольничков, а потом и ещё шесть поменьше (рис. 3, справа).

Рис. 3. Фазы изготовления заготовок

Рис. 4. Соединение граней
На рисунке 4 мы видим две уже готовые бумажные детали конструктора. Там же показан механизм соединения этих деталей-граней — они прикладываются друг к другу отогнутыми рёбрами, на которые накидывается слегка растянутая резинка.
А теперь можно приступать к большой сборке.
Тетраэдр → Октаэдр → Икосаэдр → Плоскость → ?
Начнём со сборки тетраэдра, у которого в каждой вершине сходятся по три грани, затем соберём октаэдр, в вершинах которого сходятся по четыре грани, потом икосаэдр, у которого в вершинах сходятся по пять граней (рис. 5).

Рис. 5. Тетраэдр, октаэдр, икосаэдр
Из них больше всего похож на сферу наш двадцатигранный икосаэдр, и его вполне можно было бы назвать бумажной моделью сферы.
Попробуйте теперь собрать многогранник, у которого в каждой вершине сходятся шесть треугольных граней. Тут нас ждёт первый сюрприз: оказывается, что в результате получается не многогранник, а многогранная поверхность, и если не останавливаться, то это будет бесконечная поверхность — целая плоскость. Это можно проверить экспериментальным путём — в процессе сборки, а можно просто ещё раз посмотреть на рисунок 1, чтобы понять, в чём здесь дело.
Бумажная модель плоскости Лобачевского

Рис. 6. Бумажная модель плоскости Лобачевского. При сборке она начинает сильно извиваться
А теперь посмотрим, что скрывается за знаком «?» в заголовке предыдущего раздела. Для этого при сборке многогранника в каждой вершине будем соединять по семь треугольных граней. Здесь опять возникнет бесконечная многогранная поверхность (рис. 6), и, как мы увидим, она будет служить неплохой моделью для плоскости Лобачевского.
На рисунке 6 собран небольшой кусок поверхности, но уже видно, что с ростом числа граней она начинает сильно извиваться и целиком не сможет разместиться в нашем трёхмерном пространстве — в некоторый момент её сборка застопорится. Таким же свойством обладает и настоящая плоскость Лобачевского, её тоже нельзя разместить в трёхмерном пространстве, — это известная теорема Гильберта.
Изучение нашей модели начнём с того, что попытаемся нарисовать на ней прямую. Вот как это можно сделать. Сначала на выбранной треугольной грани с помощью линейки проведём отрезок прямой. Для продолжения отрезка на соседнюю грань выровняем обе грани, чтобы они лежали в одной плоскости, и с помощью линейки продолжим наш отрезок на соседнюю грань. Это первый шаг, но, повторяя его раз за разом, можно неограниченно продолжить отрезок в одну сторону, и так же в другую — получится бесконечная прямая. Но не всегда, а только если мы ни в какой момент не попадём в вершину треугольника. В вершине нам не удастся одновременно выровнять все семь треугольников. Максимум можно выровнять пять треугольников, причём двумя разными способами. Тем самым, прямая продолжается неоднозначно.

Рис. 7. Проведение прямой
Удобно считать, что сторона поверхности, видная на рисунке 6, это изнанка, а на противоположной гладкой стороне будем рисовать, как это сделано на рисунке 7. Наша модель благодаря резинкам обладает упругими свойствами, заставляющими её изгибаться, поэтому, проводя прямую, желательно прижимать конструкцию линейкой.
После того как мы научились рисовать прямые, можно строить треугольники. На маленьком кусочке нашей модели с одной вершиной посередине, где сходятся семь граней, нарисованы два треугольника (рис. 8).

Рис. 8. В одном треугольнике сумма углов равна 180°, в другом 120°
Возьмите транспортир и измерьте на своей модели сумму углов в каждом из них. В том треугольнике, который не содержит вершины, сумма углов равна 180°, как в обычном треугольнике на обычной плоскости. В другом треугольнике сумма углов равна 120°. Если внутри треугольника будут содержаться две вершины поверхности, то сумма углов в нём будет равна 60°. А треугольников, содержащих внутри себя больше двух вершин, на нашей поверхности просто не существует.
На настоящей плоскости Лобачевского происходят аналогичные вещи. Во-первых, там сумма углов любого треугольника меньше 180°, во-вторых, площадь любого треугольника не может превосходить некоторого фиксированного числа. Второй факт как раз соответствует тому, что у нас внутри треугольника не может лежать более двух вершин.

Рис. 9. Эти параллельные прямые наиболее близки в одном месте и расходятся при удалении от него
А теперь о самом интересном — о параллельных прямых, то есть о прямых, которые не пересекаются. Посмотрите на рисунок 9, где нарисованы две непересекающиеся — параллельные прямые. Видно, что в некоторый момент они расположены близко друг к другу, но при удалении и в одну и в другую сторону от этого места они начинают расходиться. Это происходит на нашей поверхности, но это также характерное поведение параллельных прямых на плоскости Лобачевского.
Правда, на нашей модели есть и исключения из этого правила. Если в полосе между параллельными прямыми нет ни одной вершины поверхности, то эти прямые всё время остаются на одном и том же расстоянии друг от друга (рис. 10).

Рис. 10 (слева). Эти две параллельные прямые всё время остаются на одинаковом расстоянии друг от друга. Рис. 11. Через точку вне нижней прямой проходят две прямые, параллельные данной (не пересекающие её)
И наконец, о самом главном — о том, что на обычной плоскости через точку, не лежащую на данной прямой, можно всегда провести одну и только одну прямую, параллельную данной, а на плоскости Лобачевского это не так. Не так это и на нашей модели, и рисунок 11 отчётливо демонстрирует это.
На этом мы закончим короткий обзор нашей модели, а в следующем номере скажем несколько слов о том, как она связана с правильными паркетами на плоскости Лобачевского.
***
В прошлом номере мы хорошо поработали с нашей бумажной моделью. Обсудили её сходство с настоящей плоскостью Лобачевского и одновременно рассказали о некоторых отличиях. А теперь мы поговорим о другой — чисто геометрической модели, которая абсолютно точно представляет собой плоскость Лобачевского, а также добавим несколько слов о правильных паркетах.
Диск Пуанкаре
Как мы уже говорили в первой части, по теореме Гильберта плоскость Лобачевского нельзя расположить в нашем трёхмерном пространстве. Но точно так же сферу или полусферу нельзя без искажений расположить на обычной плоскости. Тем не менее, у нас в распоряжении имеются удобные географические карты — плоские листы (рис. 12), по которым можно ориентироваться и с помощью простой школьной математики вычислять расстояния между различными земными пунктами.
Точно так же имеется замечательная карта плоскости Лобачевского — диск Пуанкаре. На этой карте плоскость Лобачевского тоже размещается внутри круга, и прямые на этой карте — это дуги окружностей, перпендикулярные границе круга (рис. 13). Сравните этот рисунок с рисунком 9 из первой части.
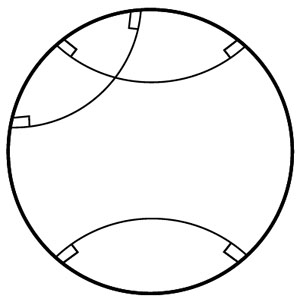
Рис. 13. Три прямые в плоскости Лобачевского изображены на диске Пуанкаре, две из прямых параллельны третьей (не пересекают её) и проходят через одну точку
Опять же плоскость Лобачевского изображается на диске Пуанкаре, то есть на обычном круге, с большим искажением, и опять же имеется несложная математика, позволяющая с помощью этой карты рассчитывать истинные расстояния на плоскости Лобачевского, а также длины окружностей, площади треугольников и других фигур и всё остальное.
Правильные паркеты
Расскажем ещё об одном замечательном свойстве плоскости Лобачевского. Помните, в первой части мы пытались из правильных треугольников составить многогранник, в каждой вершине которого сходилось бы по шесть таких треугольников, а у нас получилась целая плоскость (рисунок 1 из части 1)? Оказывается, что на обычной плоскости существует только конечное число таких паркетов, составленных из правильных многоугольников. Другое дело — плоскость Лобачевского, там их бесконечно много.

Рис. 14. Правильный паркет на плоскости Лобачевского: в каждой вершине, как и на нашей модели, сходятся семь равносторонних треугольников
На рисунке 14 представлен один из них (на диске Пуанкаре). Это ближайший родственник нашей бумажной модели, тут тоже в каждой вершине сходятся семь равносторонних треугольников, только на плоскости Лобачевского углы у них уже не по 60°, а по 360°/7.
Обратите внимание, что на этом рисунке все стороны треугольников искривлены, но так и должно быть — ведь на диске Пуанкаре они должны быть представлены дугами окружностей, перпендикулярных границе диска.
Кроме того, на первый взгляд не похоже, что длины сторон во всех треугольниках равны между собой. Но мы уже говорили, что расчёт расстояний на диске Пуанкаре происходит не так, как на обычной плоскости, и этот расчёт показывает, что все треугольники на рисунке 14 равносторонние и действительно равны между собой.
Наконец, обратите ещё внимание на то, что по мере приближения к граничной окружности треугольники визуально уменьшаются, и это говорит о том, что наиболее сильные масштабные искажения происходят именно вблизи граничной окружности диска Пуанкаре. Наверное, так и должно быть — ведь плоскость Лобачевского не помещается даже в нашем трёхмерном пространстве, а мы попытались разместить её внутри обычного круга.
Другие паркеты и другие бумажные модели
На плоскости Лобачевского существует ещё, например, паркет, составленный из правильных шестиугольников и семиугольников (рис. 15).
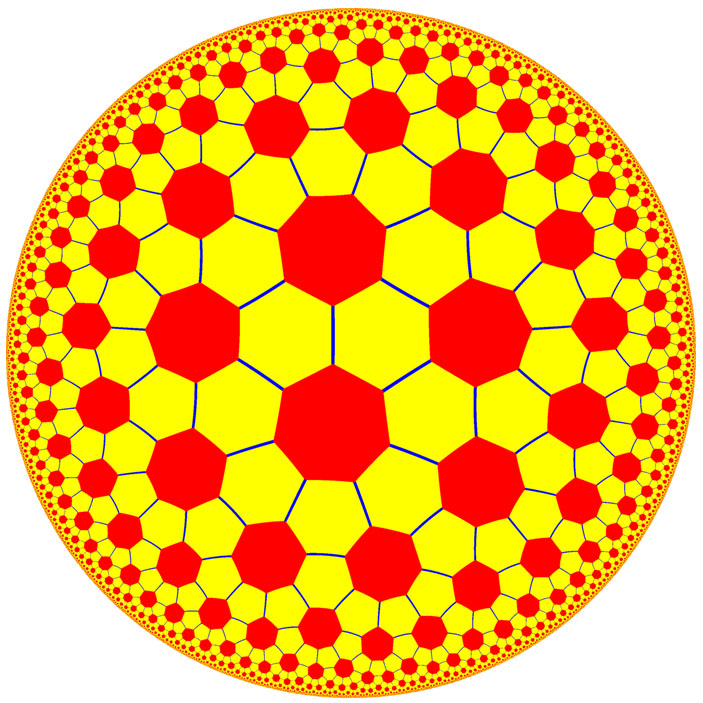
Рис. 15. Паркет из правильных шестиугольников и семиугольников на плоскости Лобачевского
Его тоже можно использовать для построения бумажной модели плоскости Лобачевского. Эта бумажная модель называется «гиперболический футбольный мяч» (hyperbolic football), и вот как она выглядит в руках математика Фрэнка Соттайла и его учеников (рис. 16). Они, кстати, скрепляют свои многоугольники не резинками, а скотчем. На фотографии все модели повернуты к нам цветной стороной, а все геометрические построения находятся на противоположной — однотонной белой. Мы тоже действовали по этому образцу, все рисунки делали на удобной — гладкой стороне.

Рис. 16. Фрэнк Соттайл со своими учениками, каждый из них держит собственноручно собранный гиперболический футбольный мяч
Сборку подобных моделей можно осуществлять и на экране компьютера. Посмотрите, как это происходит, в трёхминутном ролике под названием Growable surface, созданном Atelier Panda.
А на сайте Matematicas Visuales в разделе «Сборка многогранников из бумаги и резиновых колечек» можно познакомиться с другими красивыми объектами, собранными из конструктора, придуманного Фредом Бассетти.
В заключение приводим ссылку на сайт компьютерной игры Hyperrogue, в которой можно побродить по плоскости Лобачевского.
Фото: Валентина Асташкина
Художник Алексей Вайнер















Рис. 1. Лист ватмана разбит на треугольники. Такое разбиение, где в каждой вершине сходятся шесть правильных треугольников, называется ещё правильным треугольным паркетом