На сколько видов пентамино может делиться фигура?

Юрий Маркелов
«Квантик» №3, 2019

Рис. 1

Полимино — фигуры, образованные путём соединения нескольких клеток по их сторонам. Например, тетрамино — полимино из четырёх клеток, всего таких 5 штук (рис. 1). А полимино из пяти клеток называется пентамино, есть 12 различных фигур (рис. 2).

Рис. 2

На Математическом празднике 2018 года в 7 классе была моя задача:

Существует ли такая фигура, что при любом выборе вида тетрамино эту фигуру можно составить, используя тетраминошки только выбранного вида? (Переворачивать тетраминошки можно.)

Ответ тут положительный (рис. 3).

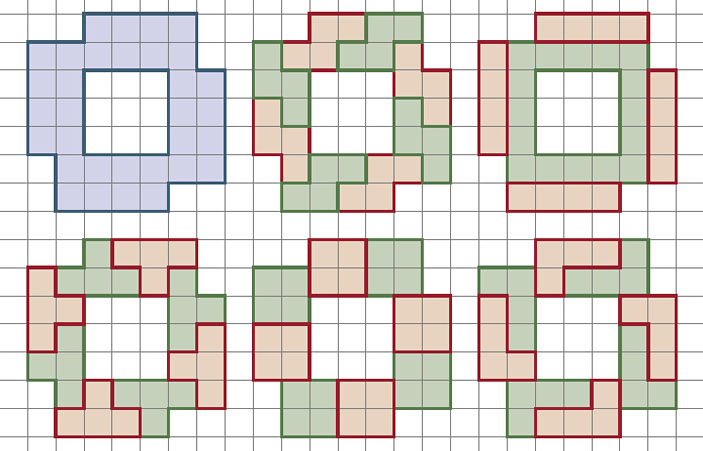
Рис. 3

Зададим тот же вопрос про пентамино. Оказывается, здесь ситуация другая: нет такой фигуры, что при любом выборе вида пентамино эту фигуру можно составить, используя пентаминошки только выбранного вида. Почему?

Докажем, что нет даже такой конечной фигуры, которая «делится» только на кресты (рис. 4) и только на арки (рис. 5). Пусть какую-то фигуру можно разделить на кресты. Рассмотрим множество самых правых её клеток, из них возьмём самую верхнюю (клетка 1 рисунка 6). В силу выбора клетки 1, фигуре не принадлежат клетки выше клетки 1 в том же столбце и все клетки правее клетки 1 (серая зона на рисунке 6). Тогда крест, накрывающий клетку 1, может стоять только как на рисунке 6. А клетки 2 и 3 не могут принадлежать фигуре, так как любой крест, содержащий одну из этих клеток и не пересекающийся с первым крестом, захватит клетку из серой зоны. Но тогда внутри фигуры не удастся расположить арку, покрывающую клетку 1.

Рис. 4, 5, 6

Рис. 7

Интересно, для какого наибольшего числа видов пентамино всё же существует фигура, «делящаяся» на каждый из них? На рисунке 7 приведён пример фигуры для 4 видов.

Точный ответ на этот вопрос нам неизвестен. Попробуйте поэкспериментировать и найти фигуру, «делящуюся» на как можно большее число видов пентамино. В следующем номере мы приведём лучший известный нам результат. Если у вас получится пример, в котором больше видов, обязательно пришлите его нам для публикации. Удачи!

Ответ

Нам известен пример Джорджа Сичермана. Придуманную им фигуру можно разделить на 8 видов пентамино (см. рисунок).

Много интересных задач и картинок с полимино и другими фигурами можно найти на сайте recmath.org.

Художник Артём Костюкевич