Как Бусенька складывала числа «в столбик»
Константин Кохась
«Квантик» №1, 2015

Не очень-то легко, оказывается, сидеть на дереве, если ветер достаточно силён. Бусенька вцепилась в ветку изо всех сил. Ветка раскачивалась, как маятник.
— Ну и непогода, — пробормотала Бусенька.
— Года два такой не было, — согласился Кто-то.
От неожиданности Бусенька потеряла равновесие и чуть было не полетела вниз. Но снизу появилось что-то, что не дало ей упасть: то ли лапа, то ли клешня, то ли хобот обвил Бусеньку и держал довольно крепко.
— Позвольте представиться, меня зовут Уккх, — сказал Кто-то.
— Укхмгм... — задрожала Бусенька.
— Не Укхмгм, а Уккх! — сказало существо. — Я питон. И можете не волноваться, сейчас я совершенно сыт.
Посмотрев на питона, Бусенька не поняла, почему это она может не волноваться. Зрелище было довольно жутким. К тому же лапа, клешня или хобот оказались хвостом питона, который по-прежнему крепко держал Бусеньку. Выбора, похоже, не было. Пришлось поверить на слово и не волноваться.
— Я — Бусенька, — сказала Бусенька. — Как вовремя вы меня подхватили.
— Я всё делаю вовремя, — сказал питон. — Не люблю опаздывать.
— А что это вы тут, на дереве, вовремя делаете в такую непогоду?
— Домашнее задание. Тема — «сложение чисел в столбик». Увлекательнейшая штука, скажу я вам.
И Уккх поднял Бусеньку повыше. Меж толстых веток, которые совсем не качались на ветру, была установлена доска и на ней написано несколько примеров.
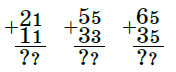
— Примеры как примеры, — сказала Бусенька, подойдя к доске. — А почему цифры разной высоты?

— Цифры? А, ну да, можно их и так называть. Видите ли, мы записываем числа очень специальным способом, он называется1 КТО(9, 7). Первая цифра — это остаток числа при делении на 9, а вторая — остаток числа при делении на 7. Поскольку 9 больше 7, мы первую цифру пишем немного крупнее — так нагляднее получается.
— Ничего не понимаю. Если я к числу прибавлю 63, получится другое число, и у него будут такие же остатки при делении на 9 и на 7, т. е. такие же цифры?
— Да. Дело в том, что мысль прибавить к числу 63 идеологически неверна! — сказал Уккх, патетически дёрнув хвостом. — Потому что способ записи КТО(9, 7) годится только для чисел от 0 до 62. Вот вы когда пишете обычные двузначные числа, вы же не можете записать с их помощью число больше 99. Зато любое число от 0 до 99 однозначно записывается с помощью двух цифр (если разрешить ноль в качестве первой цифры). И в нашей системе КТО(9, 7) каждое сочетание из двух цифр однозначно задаёт число от 0 до 62.
— Всё равно не понимаю. Вот в первом примере число 21 — что это за число?
— Да что же тут непонятного? Это то самое, единственное и неповторимое, число из диапазона [0, 62], которое при делении на 9 дает остаток 2, а при делении на 7 — остаток 1.
— Да, но что это за число? Чему оно равно?
— Вы начинаете меня беспокоить, — нервно сказал Уккх. — А я, когда беспокоюсь, сразу становлюсь голодным, так что поосторожнее с этим. Я вам полностью описал это число. С помощью моего описания оно задаётся однозначно. А вы спрашиваете, чему оно равно. Вот самому себе оно и равно!
— Но я не привыкла к таким описаниям! Я записываю числа и могу думать про них только с помощью десятичной системы счисления, а не КТО(9, 7)!
— А, вы хотите конвертировать его в десятичную систему счисления! Так бы сразу и говорили. Сейчас-сейчас, где-то тут у меня завалялась... Куда же я её дел... Вот она! — и Уккх протянул Бусеньке таблицу. — С помощью этой таблицы мы с вами с лёгкостью найдём общий язык!
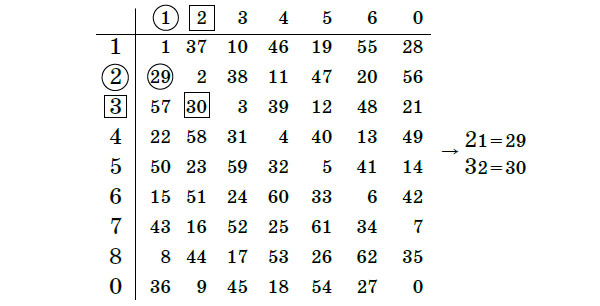
— Какой интересный способ записи, этот ваш КТО(9, 7), — сказала Бусенька, внимательно изучив таблицу. — И трудно складывать числа, записанные таким способом?
— Проще простого! Чтобы найти сумму двух чисел, надо по отдельности сложить первые две цифры и последние две цифры! Вот, например, решим первый пример, — и Уккх, взяв кончиком хвоста кусочек мела, написал на доске:

— Ну-ка я проверю, — сказала Бусенька, держа наготове таблицу. — Так, 21 — это по-нашему 29, 11 — это по-нашему, хм..., надо же, это 1. В сумме получается 30. А 30 питоша записывает как 32. И-и-и-и-и-и!!!
— Что это было?
— Как-то само собой взвизгнулось, извините, — покраснела Бусенька.
— Давайте ещё что-нибудь сложим!
— Да пожалуйста, — и Уккх записал второй пример на сложение.
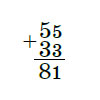
— Этот я тоже проверю, — сказала Бусенька, не выпуская таблицу из рук. — Нет, не может быть, как это? В одном случае 5 + 3 — это 8, а в другом 1?

— Ну, я забыл сказать, что есть ещё одно правило — правило непереносов. Если вы, милая аппетитная Бусенька, при сложении очередных цифр получаете сумму больше 10, вы записываете в качестве очередной цифры число на 10 меньше, чем получилось, а потом ещё делаете перенос. А у нас — всё то же самое, только без переноса! Если при сложении 2 вторых цифр получается 7 или больше, то нужно сделать неперенос — то есть отнять от этого числа 7, и всё! В нашем случае 5 + 3 = 8, отнимаем 7, получается 1. И аналогичное правило действует для первых цифр, только там вместо семи — девять.
— Тогда можно я третий пример сама решу? — торопливо спросила Бусенька, схватив мел (ей показалось, что сытость Уккха начинает уменьшаться). — Первый столбец: 5 + 5 — это 10; вычитаем 7, остается 3. Второй столбец: 6 + 3 — это 9; отнимаем... 9? Получается 0.

— Проверяем... 65 — это 33, 35 — это 12, 33 + 12 = 45, а 45 мы записываем как... вот оно, в последней строчке таблицы — как 03. Сошлось! — Уккх одобрительно кивнул и пододвинулся к Бусеньке.
— А умножать числа в такой записи тоже можно?
— Можно. Мы этого в школе ещё не проходили, но говорят, правило то же самое — отдельно перемножаем первые цифры, отдельно вторые, только вот непереносов может понадобиться больше.
— Так просто? Не может быть! Тогда давайте умножим 65 на 35!
— Не получится. Мы же работаем с числами, не превосходящими 62, а это произведение слишком большое! — сказал Уккх и облизнулся.
— Тогда давайте умножим 12 на 5. По системе КТО(9, 7) число 12 записывается как 35, а число 5 — как 55, перемножаем...

— А 64 — это по-нашему 60! Здорово! — Бусенька положила мел на место и с ужасом поняла, что его «место» — это большая обеденная тарелка. Бусенька осмотрелась. — И как это вы только догадались, что нужно рассматривать остатки от деления на 7 и на 9, чтобы построить такую замечательную систему счисления? — спросила она, приметив неподалеку от себя крепкую пружинистую ветку.
— То, что мы берём 7 и 9, как раз не очень существенно. Можно брать совершенно любые числа, лишь бы у них не было общих делителей. И не обязательно брать два числа, можно три, пять, сколько угодно — правила действий будут точно такие же. Вот только конвертировать в десятичную систему неудобно. Из десятичной в КТО — запросто, например, число 2014 по системе КТО(7, 8, 9, 11) запишется как 5671. Чтобы получить эту запись, нужно просто вычислить остатки при делении числа 2014 на 7, 8, 9 и 11. А вот перевод обратно...
Но тут Бусенька не выдержала и прыгнула прямо на ветку. Ветка спружинила и подбросила её высоко вверх. И ветер тут же понёс Бусеньку куда-то вдаль, где совершенно точно никого не интересовало, как перевести число 1235 из системы КТО(7, 8, 9, 11) в десятичную2.
Художник Инга Коржнева
1 Этот способ назван так в честь китайской теоремы об остатках.
2 Но вы всё-таки переведите.












