Сол Ле Витт: художник, который любил перебирать все случаи

Наталья Рожковская
«Квантик» № 7, 2014

В современном музее искусства наряду с пейзажами, натюрмортами и портретами можно увидеть абстрактные картины из бесформенных пятен и геометрических фигур или загадочные предметы и замысловатые конструкции из очень странных материалов. Порой даже взрослые посетители музея недоумённо пожимают плечами: «Что это? Что художник хотел этим сказать? Какой в этом смысл и почему это называется искусством?» Здесь мы оставим этот сложный вопрос без ответа, но поговорим об одном знаменитом современном художнике. Нам кажется, что его произведения могли бы заинтересовать читателей журнала «Квантик».

Речь идёт об американском художнике-концептуалисте Соле Ле Витте. Его работы оказали большое влияние на развитие искусства ХХ века. По-видимому, произведения Ле Витта никогда не выставлялись в России, но они широко известны во всем мире.

Для художника-концептуалиста самая важная часть произведения — это идея. Он стремится сделать своё творение интеллектуально интересным зрителю, во многих случаях стараясь избавить произведение от эмоций, но и не навевая при этом скуку.

Иногда, чтобы понять идею произведения, нужно обладать какой-то дополнительной информацией о творчестве художника. Но, как вы увидите ниже, идеи Ле Витта самодостаточны и связаны с математикой. Художник стремился, чтобы внимательный посетитель выставки мог увидеть идею самостоятельно, без дополнительных объяснений.

Рис. 1. «1 3 5 7 9 11»

Ле Витт любил работать с несложными геометрическими формами — кругами, квадратами, кубами, прямыми линиями. Из этих форм он составлял рисунки, причём частенько он рисовал не на холсте, а прямо на стенах музея. Также он составлял композиции из трёхмерных объектов. Многие рисунки и трёхмерные инсталляции Сола Ле Витта организованы по какому-то правилу, и зрителю предлагается отгадать это правило. Ведь это же очень интересно: подойдя в музее к какой-то группе геометрических фигур и изучив её внимательно, понять, что, оказывается, эти фигуры расположены здесь не просто так, а по какой-то закономерности.

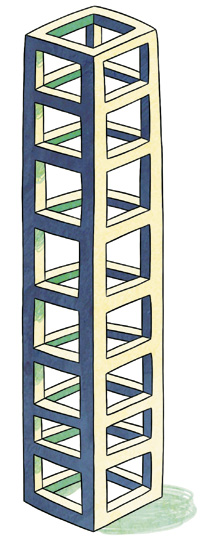
Например, посмотрите на рис. 1. Он изображает скульптуру, которая называется очень просто: «1 3 5 7 9 11». Догадались ли вы, почему?

А вот другой знаменитый проект Ле Витта (см. рис. 2). Эту роспись выставляли во многих музеях мира. Каждый раз стену раскрашивали по инструкциям художника с учётом особенностей помещения.

Рис. 2. «Настенная роспись № 260» — всевозможные комбинации из линий нескольких типов. Фото: Bava Alcide57, Викимедия

«Настенная роспись № 260» — это целая комната, где стены выкрашены в чёрный цвет и украшены узорами из белых линий (в самом первом варианте линии рисовались мелом). Узоры составлены не случайно, а по определённому правилу. Стена разбита на квадраты, и в каждом квадрате нарисована пара линий.

Каждая линия соединяет либо противоположные стороны квадрата, либо противоположные углы и имеет один из пяти типов: это либо дуга в форме четверти окружности, вогнутая в одну или другую сторону; либо прямая линия; либо пунктирная линия; либо неровная линия случайной формы:

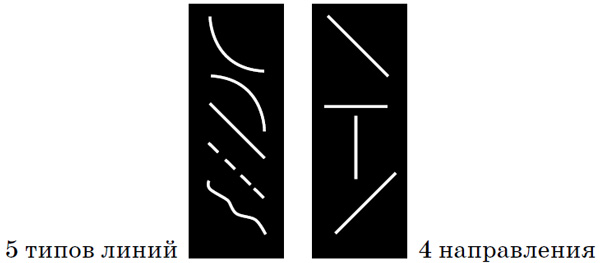
Рис. 3

Вот, например, кусочек росписи с некоторыми из возможных комбинаций (этот кусочек соcтоит из 9 квадратов):

Рис. 4

Полная роспись стены составлена из всех различных пар линий (включая даже вариант, когда пунктирная и сплошная линии в квадрате идут в одном направлении). Посчитайте, сколько всего таких комбинаций существует. Иначе говоря, из скольких квадратиков состоит роспись стены этого проекта? Ответ

Очень многие проекты Сола Ле Витта основаны на точно такой же идее: представлены все возможные комбинации объектов, обладающих какими-то свойствами. В большинстве случаев математическое описание этих проектов не представляет большого труда: так же как и для «Настенной росписи № 260», для них легко посчитать число всех возможных вариантов. Однако есть несколько проектов Ле Витта с отнюдь не очевидным комбинаторным описанием. Один из самых сложных и самых известных проектов Ле Витта называется так: «Вариации неполных открытых кубов». Он состоит из 122 скульптур, таких, как вы видите на рисунках 6–9 (схематически все 122 скульптуры изображены на рис. 5).

Рис. 5

Правило опять очень простое. Каждая скульптура — это куб, у которого убрали несколько рёбер. При этом обязательно соблюдаются следующие условия:

1. Структура должна оставаться трёхмерной. Например, плоский квадрат или просто одно ребро уже не включаются в список.

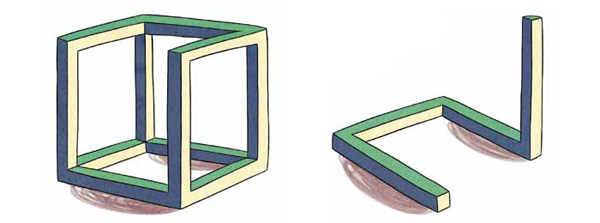
Рис. 7

2. Структура должна оставаться цельной — состоять из одного куска.

3. Две структуры считаются одинаковыми, если одну можно повернуть в пространстве и получить другую.

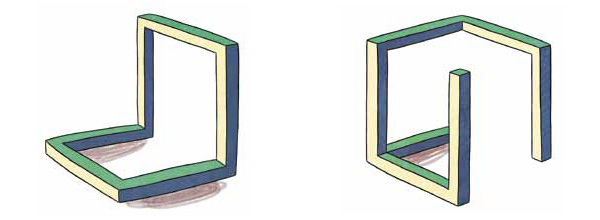
Рис. 7

Например, эти две структуры разные, они — симметричные образы друг друга:

Рис. 8

А эти структуры считаются одинаковыми, потому что любую из них можно поворотом перевести в другую:

Рис. 9

Мы не будем предлагать читателям «Квантика» проверить, что получается именно 122 открытых неполных куба, потому что этот вопрос значительно сложнее, чем, например, число комбинаций для «Настенной росписи № 260». Когда Ле Витт начинал работать над этим проектом, он не догадывался, насколько сложно будет убедиться, что все варианты учтены и ни один случай не пропущен. В конце концов, для проверки своих выкладок он перестал рисовать диаграммы на бумаге и сделал маленькие модели из проволоки. Когда художника спросили, почему он не стал искать в тот момент совета у какого-нибудь математика, Ле Витт ответил: «Во-первых, я думал, что всё будет просто и мне это не понадобится. Во-вторых, я не знал ни одного математика, которого я мог бы спросить. И в-третьих, это был некий вызов — сделать всё самому. Как в игре или головоломке, и я хотел решить её сам».

Ле Витт организовал неполные кубы в группы по числу рёбер, как показано на рис 9. По диаграммам были сделаны сами скульптуры — большие белые алюминиевые каркасы. И с тех пор многие посетители выставок художника, видя в зале эти белые остовы неполных кубов, задаются вопросами: «Не ошибся ли художник? Не пропустил ли он каких-то случаев? И почему это, казалось бы, простое правило даёт такой сложный ответ?»

Оказывается, художник почти не ошибся. Все неполные открытые кубы в этом списке нарисованы правильно, кроме одного. И мы предлагаем вам найти эту небольшую ошибку художника, посмотрев внимательно на кубы 10/4 и 10/5 (рис. 10). Утверждается, что один из этих двух кубов нужно заменить другой картинкой. Можете ли вы объяснить, какой именно и почему? Ответ

Рис. 5. Кубы 10/4 и 10/5

Заметим в заключение, что задача Сола Ле Витта относится к тому типу задач, которые требуют рассмотрения многих случаев и часто решаются перебором. Основная сложность здесь — как организовать алгоритм перебора, чтобы с ним быстро справился человек или хотя бы компьютер. Этим в какой-то степени и объясняется тот факт, что проект Ле Витта с неполными открытыми кубами оказался значительно сложнее других — комбинаторика этого проекта не описывается простыми формулами.

К слову, математики, конечно, тоже интересуются подобными задачами — они связаны с сохраняющими расстояние вложениями графов в кубы. Мы не будем сейчас объяснять, что это такое. Отметим только, что у таких вложений много хороших свойств, которые облегчают их изучение. Этот раздел комбинаторики имеет приложения в компьютерных технологиях и в химии.

Художник Наталья Гаврилова