Замощение Соколара — Тейлор

Замысловатый узор на этом рисунке — это замощение плоскости при помощи копий всего одной плитки, которую в честь описавших ее математиков называют плиткой Соколара — Тейлор. Сама плитка представляет собой обычный правильный шестиугольник, на котором прочерчено несколько линий — красных, синих и черных (три копии плитки на рисунке выделены зеленой рамкой). Они нужны для того, чтобы правильно прикладывать плитки друг к другу в процессе замощения. Если следовать двум простым правилам (о них будет сказано чуть ниже), то получающийся в итоге узор всегда будет непериодическим (то есть его нельзя совместить с собой при переносе на любой вектор). Это свойство делает плитку Соколара — Тейлор апериодическим протомножеством для плоскости. Подробнее о свойствах апериодических замощений можно узнать из картинки дня Мозаика Робинсона.

Плитка Соколара — Тейлор двусторонняя, раскраска оборотной стороны (на рисунках для удобства восприятия она закрашена серым) получается из раскраски лицевой стороны при помощи осевой симметрии и замены красных линий на синие и наоборот. На рис. 1 буквой A обозначена лицевая сторона плитки, буквой B — ее зеркальное отражение (результат осевой симметрии относительно вертикальной прямой), а буквой C — правильная раскраска оборотной стороны.

Рис. 1.

Важно, что у раскрасок A и C одинаковый циклический порядок красных и синих линий: если считать по часовой стрелке, то после двух подряд красных линий идут синяя, красная и две подряд синие линии.

Надо сказать, что сначала была придумана односторонняя реализация этой плитки (она и ее зеркальный образ, закрашенный серым, изображены ниже). Однако оказалось, что работать с двусторонней реализацией удобнее.

Соответствие между раскрасками односторонней и двусторонней реализаций плиток таково. Черные линии остаются неизменными, фиолетовые «флаги», указывающие направо (если смотреть из центра плитки), заменяются на красные линии, а «флаги», указывающие налево, — на синие линии.

Из уже сказанного ясно, что плитка Соколара — Тейлор является примером апериодического протомножества из одной плитки с раскраской и правилами стыковки, зависящими от этой раскраски. Причем это первый пример такого протомножества и найден он был совсем недавно: статья американского физика Джошуа Соколара (Joshua Socolar) и математика из Австралии Джоан Тейлор (Joan Taylor) с его описанием опубликована в 2011 году.

Близкие по духу задачи занимали математиков еще в середине XX века. Тогда не было известно, существуют ли вообще апериодические протомножества. Первый пример такого протомножества был найден американским математиком Робертом Бергером (Robert Berger) в 1966 году. В нем было 20 426 плиток, поэтому математики, естественно, стали искать примеры поменьше. И довольно быстро такие примеры были найдены: в 1971 году американец Рафаэль Робинсон придумал апериодическое протомножество из 6 плиток (см. картинку дня Мозаика Робинсона), а в 1974 году британский физик и математик Роджер Пенроуз (ставший в 2020 году лауреатом Нобелевской премии по физике) привел пример апериодического протомножества (точнее, целого семейства протомножеств) из двух плиток — это знаменитые мозаики Пенроуза. Во всех этих примерах правила составления замощения налагали ограничения только на соседние плитки (через форму выступов на их границах или требование согласованности рисунка). Для замощения Соколара — Тейлор, как станет видно чуть ниже, это не так, поэтому, вообще говоря, оно не является «одноплиточным» в «строгом» смысле. Вопрос о существовании настоящего «одноплиточного» замощения оставался открытым до марта этого года. Теперь ответ на него известен — и он положительный. Подробности описаны в новости Решена «задача Эйнштейна» о замощении плоскости («Элементы», 28.04.2023).

К слову заметим, что тема замощений — это не просто развлечение для математиков, которым хочется порисовать симпатичные картинки, а вполне серьезная область исследований. Например, как выяснилось в 1980-х годах, апериодические замощения плоскости тесно связаны с квазикристаллами (за открытие которых, сделанное в 1981 году, Дану Шехтману была присуждена Нобелевская премия по химии за 2011 год). В наше время квазикристаллы используются при создании антипригарных покрытий, в качестве покрытия для острых медицинских инструментов и как добавка в «чернила» для 3D-принтеров. Вот так стремительно — всего за каких-то полвека — был пройден путь от забавных рисуночков до применения в высокотехнологичном производстве.

Итак, что же это за правила, по которым Соколар и Тейлор разрешают составлять плитки имени самих себя? Их всего два и звучат они следующим образом:

    \(\mathcal{R}1\): Черные линии должны стыковаться друг с другом на границе плиток.

    \(\mathcal{R}2\): Возьмем любые две плитки, разделенные ровно одним ребром третьей плитки. Цветные линии, которые приходят в концы этого ребра из центров данных плиток, должны иметь разные цвета (то есть одна обязательно красная, а вторая синяя).

Первое правило, очевидно, обеспечивает, что в замощении черные линии не будут внезапно обрываться на границах плиток. Это означает, что рисунок из черных линий будет представлять собой объединение замкнутых простых кривых (в некоторых замощениях возможно такое, что черная линия уходит «на бесконечность», но таких случаев мало). Второе правило проиллюстрировано на рис. 2: «радиусы», примыкающие слева и справа к концам M и N верхней стороны центральной плитки, имеют разные цвета.

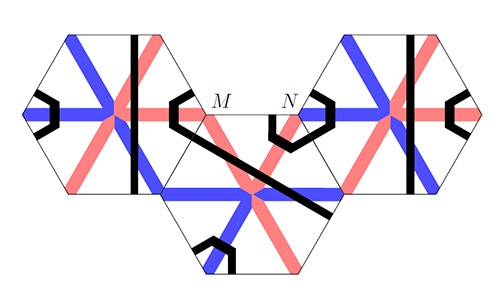
Рис. 2.

Вообще говоря, далеко не очевидно, что, следуя правилам \(\mathcal{R}1\) и \(\mathcal{R}2\), можно замостить всю плоскость без пробелов и наложений. Это требует доказательства, и оно будет дано ниже. Сначала покажем, что любое замощение, удовлетворяющее этим двум правилам, будет непериодическим.

Начнем с простого: посмотрим на черную линию, образующую «угол» в одной из вершин шестиугольника. Согласно правилу \(\mathcal{R}1\) она должна быть присоединена к другой черной линии, а следовательно, соединена либо с таким же черным «углом», либо с центральной линией другого шестиугольника. В первом случае (опять же, по правилу \(\mathcal{R}1\)) третью плитку в это место можно добавить только так, что эти черные линии замкнутся в «треугольник» (рис. 3).

Рис. 3.

Во втором случае ко второму концу черного «угла» тоже будет прилегать центральная линия («угла» там быть не может — это следует из предыдущего абзаца). Но это порождает все ту же конструкцию из двух соединенных черных «углов», только в другом месте (рис. 4, справа вверху). А значит, в замощении обязательно будет черный «треугольник» (формально он, конечно, шестиугольник, но поскольку эта деталь узора на замощении возникает при составлении трех плиток, то мы позволим себе называть ее именно так).

Рис. 4.

Будем говорить, что у такого «треугольника» размер 1. Заметим, что если вокруг одной из вершин плитки есть «треугольник» размера 1, то такой же «треугольник» есть и вокруг противоположной вершины. Это следует из правила \(\mathcal{R}2\). Пусть наша первая плитка называется A, а плитка B, образующая с ней «треугольник» размера 1, примыкает к ней слева снизу (рис. 4, внизу справа). Как может быть ориентирована плитка С, примыкающая к A слева сверху? Поскольку левое вертикальное ребро плитки A продолжается вниз красным «радиусом» плитки B, то вверх оно должно продолжаться синим «радиусом» плитки С. Легко видеть, что из-за этого к верхней вершине плитки A будет примыкать «угол» на плитке C. А раз там уже есть «угол» на плитке A, то это означает, что там неминуемо возникает еще один «треугольник» размера 1.

Отсюда сразу следует, что в любом замощении, построенном по правилам \(\mathcal{R}1\) и \(\mathcal{R}2\), «треугольники» размера 1 сами будут образовывать шестиугольную решетку, как показано на рис. 5. Обратите внимание, что на этом рисунке много пропусков (они закрашены желтым): конфигурация решетки из «треугольников» размера 1 не зависит от того, как они будут заполнены. По аналогии назовем шестиугольники этой решетки плитками размера 2 (плитки размера 1 — это те, с которых все начиналось): вершины таких плиток — «треугольники» размера 1.

Рис. 5.

Что произойдет, если теперь какой-нибудь из желтых пропусков на рис. 5 заполнить плиткой (размера 1)? Оказывается, черные линии однозначно дорисуются, — причем так, что схема их расположения в соответствующей плитке размера 2 будет идентична тому, что было на плитке, которую мы только что положили (только все линии стали в два раза длиннее). Это хорошо видно на рис. 6.

Рис. 6.

Это означает, что для плиток размера 2 также выполнены оба наших правила. А раз так, то и все предыдущие соображения тоже работают: если теперь рассматривать только плитки размера 2 (забыв про «треугольники» размера 1), то их черные «углы» тоже будут объединяться в «треугольники» (которым логично приписать размер 2), и эти треугольники сами будут образовывать треугольную решетку (рис. 7).

Рис. 7.

Эти рассуждения можно продолжать и дальше: стартовав с какого-нибудь замощения плитками Соколара — Тейлор, будем последовательно выделять в нем плитки все большего и большего размера, образованные из «треугольников» предыдущего размера. Длина стороны плитки размера \(n\) равна \(2^{n-1}\). Важно, что на каждой итерации снова будет получаться замощение, удовлетворяющее все тем же двум правилам (благодаря чему этот итеративный процесс не остановится). И здесь оказывается, что до доказательства непериодичности осталось рукой подать. В самом деле, допустим, что узор замощения (составленного из плиток размера 1) можно совместить сам с собой, передвинув его на какой-нибудь вектор \(\vec v\). Тогда должны будут совместиться сами с собой и все замощения из плиток больших размеров (ведь, по сути, это одно и то же замощение, на которое мы смотрим как бы с разных дистанций). Но вектор \(\vec v\) имеет конечную длину, а значит, есть такое \(n\), что сторона плитки размера \(n\) будет больше его длины. Но тогда при переносе на вектор \(\vec v\) эта плитка наложится сама на себя. Это противоречие и означает, что исходное замощение было непериодическим.

Несмотря на то, что замощения плитками Соколара — Тейлор не являются периодическими, они обладают свойством квазипериодичности: любой узор, составленный из конечного числа плиток, встречается в любом замощении бесконечное число раз. Для большей части узоров этот факт объясняется тем, что некоторый «треугольник» достаточно большого размера содержит такой узор целиком. Следовательно, любой «треугольник» такого же размера содержит такой же узор. А так как «треугольников» одного размера бесконечно много, то и узор внутри замощения повторяется бесконечное число раз. Может оказаться так, что некоторые исключительные узоры не содержатся ни в одном «треугольнике», однако можно доказать, что и они встречаются в замощении бесконечно много раз.

Вернемся к вопросу о существовании замощения, удовлетворяющего условиям \(\mathcal{R}1\) и \(\mathcal{R}2\). Напомним, что проблема здесь в том, что совсем не очевидно, что, начав выкладывать плитки размера 1 по этим правилам, мы рано или поздно не окажемся в ситуации, когда на какое-нибудь место будет невозможно положить плитку, не нарушив их.

Идея доказательства существования хотя бы одного замощения Соколара — Тейлор, в общем, похожа на приведенное выше рассуждение об апериодичности: точно так же будем пользоваться все увеличивающимся «масштабом» шестиугольной сетки из уже заполненной части плоскости, строя при этом замощение явно.

Начнем с того, что зарезервируем одно место для плитки размера 1, но саму ее класть не будем. Это будет «стартовой» позицией для замощения (а кавычки здесь потому, что на самом деле мы эту позицию заполним последней). Окружим ее шестью плитками (с соблюдением правил, естественно). Это породит конфигурацию, подобную изображенной на рис. 5: плитки размера 1 автоматически (коль скоро мы соблюдаем правила) выстроятся в шестиугольники с пустыми центрами («дырками»). Вершинами этих шестиугольников снова будут «треугольники» размера 1. Эта конфигурация простирается на всю плоскость и в ней точно нет никаких проблем. Также в ней, как несложно заметить, не хватает многих черных линий. Как мы сейчас увидим, эти линии будут постепенно возникать и дополняться по мере заполнения желтых дырок на рис. 5.

Заполним теперь какую-нибудь из ближайших к «стартовой» позиции дырок. В этот момент у нас есть свобода выбора ориентации плитки, которую мы туда положим. Но как только мы это сделаем, то получим плитку размера 2, которая «вынудит» заполниться сразу бесконечное число дырок — так, чтобы образовалась сетка из плиток размера 2. Продолжая дальше действовать аналогично — заполнять ближайшие к «стартовой» позиции еще не заполненные дырки так, чтобы порождать сетки из плиток все большего размера (в которых точно всё в порядке с выполнением правил), — мы будем постепенно увеличивать область, в которой дырок не остается (за исключением «стартовой»). Следующие три шага этого процесса (и получающиеся при этом плитки возрастающих размеров) показаны на рис. 8–10.

Рис. 8. Замощение плоскости «плитками» размера 2

Рис. 9. Замощение плоскости «плитками» размера 3. Справа показана сама такая «плитка» и ее сглаженный вариант

Рис. 10. Замощение плоскости «плитками» размера 4

С одной стороны, этот процесс бесконечен: сколько бы шагов мы не сделали, всегда будут оставаться дырки помимо «стартовой». С другой стороны, любая такая дырка на каком-то конечном шаге будет закрыта плиткой. Это означает, что «в пределе» мы таки покроем всю плоскость за исключением «стартовой» позиции. Важно, что при этом, ориентация (направление цветных радиусов) почти любой плитки никак не зависит от ориентации плитки, которую мы положим на «стартовую» позицию. Исключение составляют лишь плитки, лежащие на продолжениях двух из трех диагоналей «стартового» шестиугольника (это хорошо видно на рис. 10). Для завершения конструкции нужно определить направление красно-синего диаметра плитки, которую мы кладем на «стартовую» позицию, — это единственным образом задаст ориентацию этих неопределившихся плиток на продолжениях диагоналей. Этот шаг завершает доказательство существования замощения, удовлетворяющего правилам \(\mathcal{R}1\) и \(\mathcal{R}2\).

У замощения Соколара — Тейлор есть еще одно любопытное свойство, которое проявляется, если забыть про узоры из линий, а следить только за тем, какой стороной выложены плитки — «лицевой» или «обратной» (см. рис. 1). Если раскрасить стороны плитки в два цвета, то может оказаться, что в замощении есть «острова» — ограниченные области из плиток одного цвета, целиком окруженные плитками другого цвета. На рис. 11 стороны плитки окрашены в серый и черный. Два черных «острова» разного размера выделены красным, но если присмотреться, то можно найти и другие «острова» — как черные, так и серые.

Рис. 11. «Острова» в замощении Соколара — Тейлор. Рисунок из статьи Joshua E. S. Socolar, Joan M. Taylor. 2011. An aperiodic hexagonal tile

Самые маленькие «острова» состоят из 13 плиток (за характерные очертания их — а вместе с ними и «острова» больших размеров иногда называют «лама-островами»). Также бывают «острова» из 23 и 242 плиток. Существуют ли «острова» больших размеров — открытый вопрос. Также пока нет способа предсказать по части замощения, есть ли в нем «острова» и какого они размера. Зато можно определить цвет любой плитки (или, что то же самое — какой стороной она смотрит вверх), исходя из ориентации черных полос и цветных диаметров тройки шестиугольников, формирующих «треугольник» размера 1.

В заключение упомянем, что у плитки Соколара — Тейлор есть трехмерный аналог, который устроен так, что выполнение правил \(\mathcal{R}1\) и \(\mathcal{R}2\) обеспечивается только его формой. Имея набор таких «деталек», можно, как из конструктора, собирать фигуры (представляющие собой «листы» толщиной в одну «детальку»), представляющие собой полные аналоги замощений Соколара — Тейлор. Детали устроены так, что при построении замощения те из них, которые соответствуют плиткам из правила \(\mathcal{R}2\) (то есть разделенным стороной третьей плитки), касаются друг друга выступами. На рис. 12 показано, как эти детали выглядят и как они состыкуются друг с другом (цветные линии там проведены для удобства сопоставления с плиткой).

Рис. 12. Трехмерная реализация плиток. Рисунок из статьи Joshua E. S. Socolar, Joan M. Taylor. 2011. An aperiodic hexagonal tile

Казалось бы, раз есть такой хороший пространственный аналог, то почему нельзя на плоскости обойтись без «кодирования» разноцветными линиями? Дело здесь в том, что любое сечение, сохраняющее различие между наклоном синих и красных концов и параллельное основанию, разбивает деталь на несколько несвязных частей, а потому ее нельзя перевести в связную фигуру на плоскости, не прибегнув к каким-то дополнительным способам передачи информации на расстояние в одну плитку (у нас для этого использовались цветные линии). На рис. 13 приведен пример такого сечения (части одной детали покрашены на нем одним цветом). Полноценным трехмерным аналогом плитки Соколара — Тейлор, решающим задачу апериодического замощения всего трехмерного пространства, является так называемая бипризма Шмитта — Конвея — Данцера (см. Schmitt — Conway — Danzer biprism).

Рис. 13. Горизонтальное сечение замощения трехмерными «плитками». Рисунок из статьи Joshua E. S. Socolar, Joan M. Taylor. 2011. An aperiodic hexagonal tile

Михаил Грунтов, Хайдар Нурлигареев