«Вероятности и неприятности». Глава из книги

Глава 1. Знакомимся с неприятностями

Разновидности неприятностей

Какие-то наши неприятности детерминированы: случайности не играют в их возникновении ключевой роли. Например, если вам понизили зарплату на 10%, а потом извинились и увеличили на 10%, в итоге этих махинаций вы останетесь в убытке, поскольку:

Более того, если зарплату сначала повысят, а потом, не извинившись даже, понизят на те же 10%, результат выйдет таким же. Ведь совершенно неважно, в каком порядке перемножаются коэффициенты. Это очень просто, немножко обидно, но к удаче отношения не имеет.

Примером случайной, хоть и весьма вероятной неприятности может быть волшебство, происходящее в наших карманах с наушниками: кладем их аккуратно смотанными в карман, а через полчаса там происходит чудо и вынимаем мы дикий узел проводов. В 2007 году вышла серьезная научная статья двух ученых из солнечного и безмятежного Сан-Диего под заголовком «Спонтанное образование узлов на возбуждаемой нити»¹. В этой работе детально анализируется и моделируется запутывание наушников в кармане. Авторы, основываясь на теории узлов, теории вероятностей и физических экспериментах, убедительно показывают, что при стандартном способе сматывания наушники действительно должны запутываться, причем спустя всего лишь несколько секунд тряски. Впрочем, это мы и так наблюдаем почти каждый день. Сюрпризом здесь может оказаться только ожидаемая скорость запутывания.

Основной причиной образования узлов оказались, во-первых, петли, которые мы сами создаем, наматывая провод на руку, а во-вторых, три конца наушников: штекер и два динамика. В процессе случайного перемещения по карману они попадают в петли, что само по себе не страшно. Проблема возникает тогда, когда мы, пытаясь наушники распутать, тянем за эти концы. Тут-то и выясняется, что узлы на петле из веревки в трехмерном мире, раз появившись, не могут исчезнуть без нарушения целостности веревки. Пока мы трясем их, не выпуская концы наушников из рук, узлы, образованные этими концами и петлями, никуда не исчезают, а только затягиваются. Причем сами по себе петли ни в чем не виноваты. Если бы концов у наушников не было и они представляли собой замкнутое кольцо, то неразвязываемый узел образоваться бы не смог. Ведь узлы не только не исчезают, раз появившись, но и не возникают сами, если их изначально не было.

С этой неприятностью вполне можно бороться математическим способом: нужно либо исключить концы, что в случае наушников неинтересно, либо убрать петли. А это можно сделать с помощью операции сложения. Но не той, что мы изучали в школе, а той, что применяется к петлям на веревках и лентах. Как и числа, петли бывают разных знаков, причем для каждой «положительной» можно построить такую «отрицательную», что в сумме они дадут «ноль»: прямую веревку. Примеры таких петель показаны на рис. 1.

Рис. 1. Примеры сложения петель разных знаков

Попробуйте мысленно нанизать на шнурок несколько таких петель разных знаков и вычислите результат и его знак. Чтобы наушники не запутывались, число положительных и отрицательных петель должно оказаться равным. Таких способов сложения проводов несколько, один из них показан на рис. 2. Здесь петли разных «знаков» появляются сразу парами и взаимно уничтожают друг друга, не формируя узлов. Уже много лет я складываю наушники именно так, чувствуя себя крутым топологом, и всякий раз радуюсь как фокусу, когда они сами собой полностью разматываются от одного небрежного встряхивания рукой.

Рис. 2. Один из способов складывания проводов, не приводящий к их запутыванию. Он хорош еще и тем, что попутно вы складываете пальцы в мудру любви

Но и среди стохастических по природе законов не все одинаково интересны. Например, закон Бука («Ключи всегда находишь в последнем кармане») не имеет рационального основания. Простой подсчет показывает, что при равной вероятности отыскать ключи для всех карманов последний ничем не отличается от прочих. Впрочем, этот закон можно трактовать разве что как забавный трюизм: утверждение Бука верно всегда, поскольку тот карман, в котором ключи будут обнаружены, окажется завершающим в процессе поиска и, следовательно, последним. Однако и здесь есть о чем поговорить. В процессе перебора карманов так называемая условная вероятность того, что ключи лежат в последнем из них, действительно повышается. Но это уже нельзя трактовать как вероятность того, что ключи находятся в последнем кармане, тут уже другая задача. Мы вернемся к этому примеру в главе 5.

Нас будут интересовать законы парадоксальные и поучительные, те, которые выглядят злым роком, выбирающим из множества вариантов самые досадные и неприятные, наперекор интуиции, подсказывающей, что этот вариант не должен быть самым вероятным. И, прежде чем приступить к детальным и точным рассуждениям о случайностях и вероятностях, предположим, что какая-то интуиция в отношении случайных процессов и вероятностей у нас уже есть. Это вполне допустимо даже в математической книге — до какого-то момента использовать интуитивное представление о предмете, а потом дать строгое определение. Тем самым, во-первых, мы определяем границы применимости нашей интуиции, а во-вторых, расширяем их в правильном с научной точки зрения направлении. Но не будем забывать о законе Вертерна: «Предположение — мать любой неразберихи», и все наши гипотезы и даже строгие выводы постараемся, где возможно, проверять с помощью имитационного моделирования.

А при чем тут математика?

Петли, наушники, законы подлости, неприятности... при чем же тут математика? Почему вообще имеет смысл рассуждать о законах подлости не так, как Артур Блох, когда он просто посмеялся и нашел меткий афоризм?

С математикой знакомы все, но мало кто готов ответить на вопрос: что делают математики? Считают и вычисляют? Рисуют треугольники и круги на бумаге в клеточку? Передвигают туда-сюда буквы в уравнениях? Придумывают странные значки и закорючки, чтобы потом писать непонятные тексты? Решают задачи, вычисляя что-то по заказу инженеров, медиков, химиков и других практиков?

Если вы никогда этого не делали, загляните в какой-нибудь математический журнал — просто из любопытства. Сейчас это легко сделать не выходя из дома: поищите в Сети что-то на тему «гомологическая теория типов» или «топология». Вы поразитесь тому, насколько то, что вы там обнаружите, не похоже на школьный образ математики. Но вот что важно: эта колоссальная разница не говорит о том, что есть одна, «простая» математика и другая, «сложная». Математику часто называют языком. Как на любом живом человеческом языке можно писать анекдоты и незамысловатые детские стишки или неуловимо тонкую поэзию, тяжеловесный роман или многостраничный договор, так и с помощью математики можно рассуждать о числах и отрезках, а можно — о петлях и поверхностях, многомерных пространствах и даже основах самой этой науки. Не нужно думать, что числа и отрезки — самое простое, с чем работают математики! Современные теория чисел и геометрия — огромные и во многом неизведанные области, в которых ведутся очень интенсивные исследования.

Но что же все-таки изучают математики? Для чего им этот язык? Чаще всего речь идет о тех или иных моделях. Например, что может быть моделью количества? Число, скажете вы. Но любое ли число годится для этого? Младшие школьники, впервые сталкиваясь с отрицательными числами, испытывают замешательство, ведь модель числа оказывается шире привычного им понятия количества. Переход от количества к шагам помогает понять, что числа годятся для моделирования движений на прямой. Тогда отрицательные числа обретают наконец смысл. А чем можно моделировать скорость? Тоже числом. Но если я скажу вам, что двигаюсь со скоростью 60, будет ли этого достаточно для описания того, что со мной происходит? Точно нет! Остается неясно ни куда я двигаюсь, ни, собственно, с какой скоростью: 60 может означать как 60 км/ч, так и 60 мм/год. Отсюда можно заключить, что для моделирования скорости только числа недостаточно. А если, желая объяснить вам, как я перемещаюсь, я изображу стрелку, станет ли понятнее? Стрелка — ориентированный отрезок — в качестве модели скорости лучше. Она показывает направление, а сравнив ее с какой-то эталонной стрелкой, принятой за единицу, можно определить ее масштаб. Более того, стрелки можно складывать и умножать на числа, получая новые корректные стрелки! И, главное, если мне удастся придумать, как однозначно сопоставлять скорости предметов стрелкам на бумаге, причем окажется, что если \(v_1\) соответствует стрелка a, а скорости \(v_2\) — стрелка b, сумме скоростей \(3v_1 + v_2\) будет соответствовать стрелка 3a + b и никакая иная, — то это уже будет свойством, позволяющим мне не бегать по двору, изучая скорости, а, сидя в кресле, рисовать стрелки на бумаге.

А можно ли чем-то моделировать стрелки? Абстрактной моделью в этом случае способен стать упорядоченный набор чисел с определенными правилами сложения и умножения на число, который называется вектором. Так математики пришли к мысли о линейных векторных пространствах, элементами которых являются векторы. Изучая свойства этих пространств (изучая, а не придумывая, разницу мы обсудим позже), математики выработали единый язык, который называется линейной алгеброй, для разговора о таких разных вещах, как, например, цвета, вращения предметов в пространстве, спектры звуковых сигналов. Пользуясь этим языком, уже можно найти оптимальную стратегию в экономической игре или научить компьютер распознавать нашу речь, рукописные буквы либо лицо человека в толпе.

Математики работают с математическими структурами — универсальными моделями всего, с чем имеет дело человеческий разум. Группы, поля, решетки, графы, петли, косы, языки и бесконечномерные пространства... Все это структуры с четко определенными свойствами и, если угодно, поведением. Вот уже тысячи лет математики исследуют взаимосвязи между ними, обнаруживают в реальном и математическом мире, что еще можно с их помощью моделировать и при каких условиях.

Я не случайно называл манипуляции с петлями на проводе наушников «сложением», а сами петли «положительными» и «отрицательными». Такая терминология оправдана тем, что петли на струне образуют структуру, называемую группой. Для ее построения нужно иметь множество² A и некую операцию +, которая будет удовлетворять следующим четырем свойствам.

1. Замкнутость: для любых двух элементов из множества A результат операции + всегда будет элементом этого же множества.
2. Ассоциативность: для любых a, b, c из множества A верно, что \((a+b)+c=a+(b+c)\)
3. Существование нейтрального элемента: в A есть единственный элемент 0, такой, что \(0+a=a+0=a\) для любого a из A.
4. Обратимость: для каждого элемента a в A существует единственный обратный ему элемент \((-a)\), такой, что \(a+(-a)=0\).

Группа — общая модель для обратимого ассоциативного комбинирования действий или объектов. Ее образуют числа с операцией сложения, и они же формируют группу с операцией умножения. Несложно убедиться, что аксиомам группы удовлетворяют и петли на веревке или ленте. Понятие группы настолько важно в математике, что, хотя они сами нам в этой книге и не понадобятся, нелишним будет о них рассказать тем, кто с таким подходом еще не знаком, или напомнить тем, кто о группах уже слышал, но не связал свою жизнь с их изучением.

Мы в основном будем иметь дело с двумя структурами: случайными величинами и случайными функциями. Но, знакомясь с ними, мы встретим многие другие понятия и модели и обозначим некоторые связи между ними.

А начнем мы с простого инструментария, который будет полезен на протяжении всего рассказа. И для этого нам потребуется... велосипед!

Закон велосипедиста

Я большой энтузиаст любительского велосипедного спорта. Многие задачи, вошедшие в эту книгу, я обмозговывал в седле, вертя их мысленно и так и эдак, пытаясь найти наиболее наглядный и простой подход к их объяснению. Что может быть лучше, чем мчаться по трассе ранним утром, по холодку, скатываясь с легкого склона... Это ощущение стоит того, чтобы ради него преодолевать бесконечные подъемы или сопротивление встречному ветру! Правда, порой кажется, что подъемов больше, чем спусков, а ветер норовит быть встречным, куда ни поверни. В книгах по мерфологии в связи с этим приводится закон велосипедиста:

Независимо от того, куда вы едете, — это в гору и против ветра.

Живу я на Камчатке. В Петропавловске много горок — катаясь по городу, их не миновать. Однако меня должна успокаивать такая мысль: начиная свой путь из дома, я возвращаюсь снова туда, а это значит, что суммарный спуск должен быть равен суммарному подъему. Особенно честным будет маршрут, в котором прямой и обратный пути совпадают.

Представим себе 2-километровую трассу, которая состоит из одной симметричной горки: километр вверх, километр вниз. Вверх по склону я могу достаточно долго ехать со скоростью 10 км/ч, а на спуске стараюсь держать скорость 40 км/ч (я осторожный велосипедист). Исходя из этих условий, на подъем я буду тратить в четыре раза больше времени, чем на спуск, и общая картина получится такой: 4/5 времени путешествия уйдет на тягучий подъем и лишь 1/5 — на приятный спуск. Обидно — 80% времени прогулки займет сложный участок пути! Этот результат не зависит от длины горок, а определяется лишь соотношением скоростей. Если я выкачусь из нашего холмистого города в сторону океана или в долину реки Авачи, горок почти не будет, но в моем распоряжении остаются встречный и попутный ветер или участки с плохой дорогой, которые также способны отнять значительную часть времени путешествия.

Взглянем на закон велосипедиста несколько иначе. Если я сделаю множество селфи на протяжении своей велопрогулки в случайные моменты, а потом займусь их подсчетом и классификацией, то обнаружу, что большинство картинок показывает мне согбенную фигуру в оранжевом шлеме, упорно ползущую вверх по склону либо сопротивляющуюся встречному ветру. Доля снимков с летящим и сияющим велосипедистом, как на рекламной картинке, увы, составит лишь около 20%. А что скажет статистика? Если мы выпустим на холмистую трассу большую толпу велосипедистов, подождем немного и понаблюдаем за их плотностью, то увидим, что бoльшая часть спортсменов толпится на трудных участках, а доля безмятежно улыбающихся лиц не так уж и велика!

Измеряем уровень подлости

Давайте, как когда-то в школе, покажем на графике зависимость перемещения велосипедиста от времени при движении по симметричной треугольной горке. Только сделаем всё «по-взрослому», в так называемых собственных масштабах задачи³: расстояние станем измерять не в километрах, а в долях общего пути. Так же поступим и со временем путешествия. Первую половину пути велосипедист двигался медленно и долго — 4/5 всего времени, — а вторую преодолел быстро — за 1/5 времени (рис. 3).

Рис. 3. Диаграмма перемещения велосипедиста в долях от общего пути и времени

Что же нам показывает полученный график? Во-первых, мы можем сравнить скорости на разных участках (наклоны) со средней скоростью, которая соответствует диагональной линии. Во-вторых, становится наглядным соотношение 80/20 — 80% времени путешествия заняла трудная половина маршрута. Кроме того, из графика можно заключить, что за первую половину расчетного времени путешествия велосипедист успеет преодолеть лишь треть пути. Пока все предельно просто и понятно.

А что, если маршрут велосипедиста усложнится и перестанет быть симметричным? Что, если участков с подъемами и спусками окажется несколько, и все они будут разными по сложности? Можно изобразить путешествие и на этот раз — например, так, как показано на рис. 4.

Рис. 4. Диаграмма перемещения велосипедиста для более сложного маршрута

Диаграмма хорошо отражает характер пути, но не дает представления об общем соотношении легких и трудных участков; иными словами, она ничего не говорит о распределении скоростей. О том, какой смысл мы вкладываем в слово «распределение», речь пойдет в следующей главе; пока же доверимся интуиции и тому, что мы используем его достаточно часто и порой не вкладываем в него точный математический смысл. Чтобы увидеть это распределение, упорядочим отрезки пути по скорости от самых медленных до самых быстрых, после чего вновь нанесем их на диаграмму (рис. 5).

Рис. 5. Диаграмма перемещения велосипедиста для распределения скоростей

Мы потеряем при этом информацию о последовательности участков, зато получим обобщающую картину, отражающую то, что можно было бы условно назвать «справедливостью» распределения. Более того, если вместо одного велосипедиста мы взглянем на группу спортсменов, ездящих по этому маршруту в произвольном направлении, то наша диаграмма практически не изменится, разве что несколько сгладится из-за разброса скоростей. Ее смысл останется прежним: она покажет, насколько этот маршрут отклоняется от самого справедливого, на котором время преодоления участка не зависит от его «трудности», а определяется только его длиной.

Пора пояснить, откуда взялась такая странная терминология. С начала XX века у эконометристов, демографов, экологов и маркетологов появились вполне универсальные способы суждения о несправедливости этого мира — кривая Лоренца и связанный с ней индекс Джини.

Для известного распределения в некоторой популяции чего-нибудь ценного, например денег, можно, отсортировав элементы множества по возрастанию уровня богатства, построить кумулятивную кривую. Она строится путем последовательного суммирования вкладов каждого члена группы и показывает, как по мере добавления новых членов растет общее благосостояние популяции. Далее нужно поделить все значения, отмеченные по оси X, на численность популяции, а по оси Y — на общее ее благосостояние, перейдя от конкретных чисел к долям или процентам. Получится кривая, носящая имя американского экономиста Макса Отто Лоренца. Когда мы строили график перемещения велосипедиста по простой треугольной горке, мы, по существу, создали кривую Лоренца для распределения скоростей по отрезкам пути, состоящего всего из двух столбцов, как показано на рис. 6.

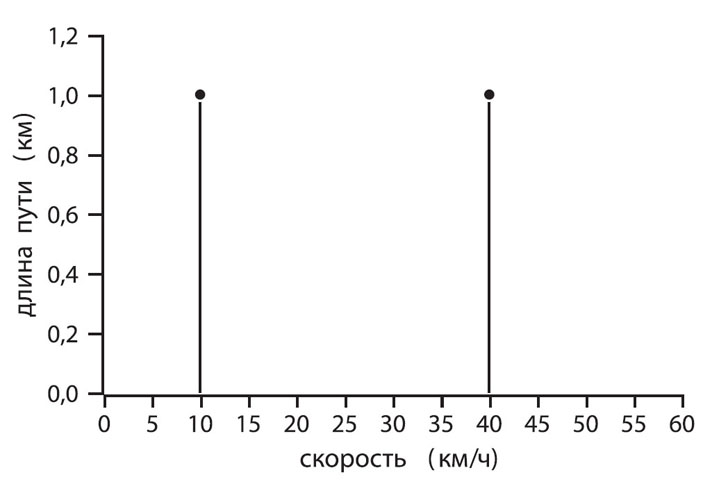
Рис. 6. Распределение скорости велосипедиста по пройденному пути

Конечно, не всякий график перемещения можно воспринимать как кривую Лоренца. Для начала нужно отсортировать периоды путешествия по возрастанию скорости, после чего приступать к построению. Можно построить гистограмму скоростей, сгруппировав известные нам данные по принадлежности к известным интервалам значений, после чего последовательно суммировать вклады всех данных гистограммы, начиная с малых значений и заканчивая самыми большими. Результатом должна стать всюду вогнутая кривая, которая проходит ниже диагонали, — настоящая кривая Лоренца. Упомянутая диагональ называется кривой равенства, она в нашем случае соответствует постоянной (средней) скорости на всем пути или гистограмме с единственным столбиком (такое распределение называется вырожденным). В экономическом контексте кривая равенства отражает всеобщее равенство благосостояния в обществе. Чем больше кривая Лоренца отклоняется от кривой равенства, тем менее «справедливым» можно считать распределение. И, раз уж мы изучаем законы подлости и несправедливости нашего мира, разумно использовать терминологию и инструменты, созданные именно для исследования справедливости.

Площадь под кривой Лоренца для любого невырожденного распределения будет меньше площади под кривой равенства. Их разница может служить формальной характеристикой неравенства или «несправедливости» распределения. Эту роль на себя берет индекс Джини. Он вычисляется как удвоенная площадь замкнутой фигуры, образуемой кривой равенства и кривой Лоренца (ее мы показали заливкой на рис. 5), и лежит в диапазоне от 0 до 1. Для кривой равенства, идеального вырожденного мира, индекс Джини равен 0, а в самом кошмарном варианте, когда все богатство группы принадлежит одному ее члену, он равен 1. В рассмотренном нами примере он составляет 0,35. Это неплохой показатель. Скажем, распределение богатства среди населения в России сейчас имеет индекс Джини 0,39, в США — 0,49, в Австрии и Швеции не превышает 0,3, а для всего мира он в 2017 году составил 0,66. Так что приведенная нами в качестве примера ситуация с велосипедистами, конечно, несправедлива, но вполне терпима.

Обратите внимание на то, что с помощью некоторого формального индекса мы стали сопоставлять совершенно разные и несравнимые вещи. Это одновременно и заманчиво, и опасно. Нужно отдавать себе отчет в том, что формальные индексы и числовые показатели всегда чему-то равны, независимо от того, есть в этом какой-либо смысл или нет. Мы сравниваем распределение богатства среди населения стран и распределение времени, затрачиваемого на преодоление пути, с точки зрения отличия от некоторого варианта, который сочли бы справедливым. Пока мы ведем фривольные и подчас хулиганские разговоры о законах подлости, пожалуй, это оправданное сравнение; но в науке так, конечно, делать нельзя. Кривую Лоренца и индекс Джини можно формально рассчитать и для гистограммы яркости пикселов на картинке или для частотности слов в живой речи. Но к справедливости это не будет иметь никакого отношения, да и смысла останется совсем немного, поэтому, имея в виду индекс Джини для чего попало, мы будем его называть индексом подлости, чтобы не вводить читателя в заблуждение наукообразностью терминов.

Кривые Лоренца и индекс подлости позволят нам смело сравнивать возмутительно разные вещи. Математика — точная наука, но никто не запрещает математикам хулиганить. В своем, конечно, кругу и без драк.

От закона велосипедиста к парадоксу инспекции

Вывод, который делает велосипедист, пыхтя на пониженной передаче: «Мир несправедлив, бoльшую часть сил отнимает самая дурацкая часть работы», — часто именуют принципом Парето или принципом «80/20»: «80% усилий дают 20% результатов». Это абсолютная эмпирика: принцип Парето никто не доказывал, но его так часто цитируют, что он уже производит впечатление истины. Его используют и как оправдание неудачам, и даже как инструкцию, обнаруживают в самых разных проявлениях. Иногда это работает: например, принципу «80/20» соответствует индекс подлости около 0,6, как для распределения богатства в мире.

У принципа Парето есть полезное для понимания более строгое обобщение. Закон подлости, названный Артуром Блохом в честь безымянного велосипедиста, имеет официальное научное звание: парадокс инспекции. Это хорошо известное явление встречается в разных исследованиях, связанных с социологическими опросами, тестированием, и в теории отказов (разделе прикладной математики, занимающемся надежностью сложных систем), неявно, но систематически смещая наблюдаемые результаты в сторону наиболее часто наблюдаемых явлений.

Приведем классический пример, связанный с неудовольствием пассажиров общественного транспорта. На линии в некоем городе работает множество автобусов. В относительно короткий час пик они переполняются, всё же остальное время ходят почти пустыми. Если мы станем опрашивать пассажиров, то выясним, что бoльшая их доля оказалась невезучей и ехала в переполненном транспорте (по той простой причине, что в переполненном автобусе было больше людей), и получим выражение общего недовольства. Если же мы опросим водителей, то они тоже начнут жаловаться, но, как ни странно, на незаполненность большинства маршрутов и неразумность руководства, гоняющего их попусту. Гибкий график сгладит ситуацию, но в любом случае кривая Лоренца будет отклоняться от кривой равенства, соответствующей невероятной ситуации всегда одинакового числа пассажиров во всех автобусах.

В учебниках по теории вероятностей часто встречается специальный непрозрачный мешок, в который математики складывают разнообразные объекты, а потом наугад вытаскивают их, делая подчас весьма глубокомысленные выводы. Разрешение нашего парадокса в том, что, анализируя систему пассажиропотока в целом, мы кладем в мешок автобусы, а проводя опрос, достаем из него наугад пассажиров и по их данным пытаемся делать выводы об автобусах. Рисунок 7 показывает, в чем тут разница.

Рассмотрим эту ситуацию подробнее, построив кривую Лоренца (на этот раз настоящую) для числа пассажиров в автобусах, показанных на рис. 7.

Рис. 7. Статистика по автобусам говорит, что в 75% машин есть свободные места, то есть они ходят не в полной мере эффективно. А опрос пассажиров обнаружит, что 61% людей, воспользовавшихся автобусом в этот день, оказались в переполненном транспорте и остались недовольны

Для этого нужно отсортировать машины по числу пассажиров и последовательно суммировать вклад каждого в общий пассажиропоток.

Полученные кумулятивные суммы следует разделить на их максимальные значения, чтобы получить доли, например, в процентах, после чего их можно нанести на диаграмму (рис. 8).

Кривая Лоренца в данном случае показывает, как распределение числа элементов в некоторых группах (горизонтальная ось) смещается при анализе распределения элементов по принадлежности к группам (вертикальная ось). В этом, собственно, и состоит парадокс инспекции: картинка, которую наблюдает инспектор, оказывается искаженной. Ведь он анализирует не группы, а их элементы, и при этом наблюдаемые значения смещаются в сторону более «весомой» части распределения.

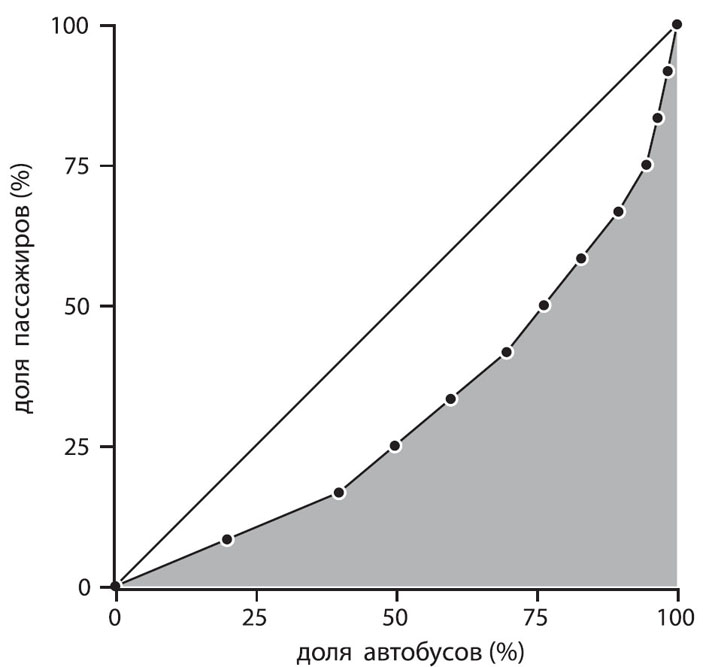
Рис. 8. Кривая Лоренца хорошо иллюстрирует несправедливость ситуации с автобусами: половина возит лишь четверть всего пассажиропотока, а на 25% перегруженных машин приходится половина пассажиров

Сам по себе закон велосипедиста очень прост, но он то и дело будет усугублять другие законы подлости, прибавляя им угрюмой эмоциональной окраски. Размышляя об этом, мне нравится представлять, как искажается восприятие мира инспектором, становясь контрастнее. В растровых графических редакторах есть инструмент «Кривые». Он позволяет дизайнеру или фотографу тонко менять контраст картинки, манипулируя распределением числа пикселов по яркости. Вот, например, как меняет восприятие реальности кривая Лоренца, полученная нами для автобусов. Картина мира становится мрачнее, как мы и ожидаем (рис. 9).

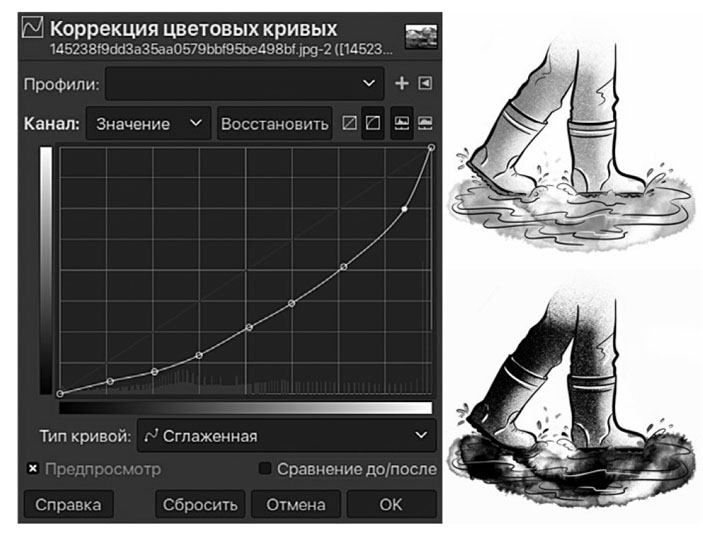
Рис. 9. Кривая Лоренца, примененная в качестве фильтра «Цветовая кривая» в растровом графическом редакторе, делает любую картину мрачнее

Крайнее проявление парадокса инспекции возникает, если в группах, помещенных в наш теоретический мешок, есть не просто редкие элементы, а элементы, не наблюдаемые вовсе. Тогда мы получаем то, что статистики, демографы и публицисты называют систематической ошибкой выжившего.

Часто ее демонстрируют на примере с дельфинами, которые спасают людей, оказавшихся волею несчастного случая в открытом море. Дельфины обнаруживают на поверхности моря любопытный несъедобный объект (человека) и играют с ним, подталкивая носом. При этом они необязательно толкают его в сторону ближайшего берега — часть людей они уводят в открытое море, поскольку разумно предположить, что для дельфина берег, да еще и населенный людьми, опасен. Однако, если всё же дельфины толкают потерпевшего именно к берегу, в сторону спасения, и он благодаря этому выживает, весь мир облетает новость: дельфины спасли человека! О поведении дельфинов во всех прочих печальных случаях, увы, мы не узнаем ничего. Эти элементы из мешка мы не достанем и в статистику они не попадут, так что мы получим явно искаженную картину.

Об этом явлении часто рассказывают в различных демотивирующих статьях для начинающих бизнесменов, уверяя их в том, что успешный путь, описываемый в мотивационных книгах, скорее всего, не для них: «неудачники книг не пишут». Впрочем, к законам подлости это отношения не имеет, тут мы касаемся психологии. Парадокс инспектора и ошибка выжившего действительно способны искажать восприятие действительности, омрачая ее либо придавая излишне радужную окраску. Но с научной точки зрения это методические ошибки при получении и обработке данных. К сожалению, они приводят к расхожему мнению о статистике как нечестном манипулировании фактическими данными среди людей, весьма далеких от этих методик. О таких ошибках знать полезно, чтобы избегать их в своей работе и критически относиться к новостям, слухам и недобросовестным исследованиям. Этой теме посвящена относительно недавняя книга Джордана Элленберга «Как не ошибаться»⁴, содержащая множество ярких примеров того, как статистические данные и числа могут быть до забавного неверно поданы и интерпретированы.

* * *

Мы встретимся с парадоксом инспекции и его влиянием еще не раз: стоя в очереди или на автобусной остановке, рассуждая о судьбе. Поняв, что это не козни рока, а простейшая математика, с которой бороться смысла нет, можно научиться получать удовольствие и от затяжных подъемов, и от нудных, но неизбежных этапов работы — хотя бы решая в уме задачи или медитируя. Даосы стремились жить вечно и верно рассудили, что вместе с работой над телом для достижения их цели требуется подготовка ума. Ведь для вечной жизни нужно не только умение отпускать привязанности, но и терпение, а также способность получать удовольствие от затяжных участков.

¹ Raymer D. M., Smith D. E. Spontaneous knotting of an agitated string // PNAS. October 16, 2007. Vol. 104. No. 42. Pp. 162–167.

² Полагаю, читатель знаком с понятием множества, а также с отношениями и операциями над множествами: пересечением, объединением и пр. Для понимания книги это не обязательно, но для понимания современной математики строго необходимо. Так что любопытного неофита я отсылаю к списку литературы в самом конце книги, а еще лучше — к преподавателю. Поверьте, если школьного учителя попросить растолковать вам, что такое множества и что с ними можно делать, вы оба получите удовольствие!

³ Подробнее о собственных масштабах и обезразмеривании задачи мы поговорим в главе 2, когда речь пойдет о бутербродах.

⁴ Издана на русском языке: Элленберг Дж. Как не ошибаться. Сила математического мышления. М. : Манн, Иванов и Фербер, 2017.